OpenCity: Open Spatio-Temporal Foundation Models for Traffic Prediction

csjywu01 / 2024-10-23 / 原文

1. 数据准备

在这个数据处理过程中，以数据集 PEMS07M 为例，整个数据抽取和划分过程如下：

初始数据维度：
- 原始训练数据 data_train 的维度为 (12672, 228, 3)。其中：
  - 12672 表示时间步数，代表不同的时间点采样的数据。
  - 228 表示空间节点数（例如不同的交通站点）。
  - 3 表示每个节点在每个时间步的特征数量。
滑动窗口机制：
- 在初始化 TrafficDataset 时，设置了 input_window=288 和 output_window=288，这意味着每次取出连续的 288 个时间步作为输入数据（input），接着取出后续的 288 个时间步作为输出数据（output）。
- 举例说明，如果 i=0，input 会是 data[0:288]，output 会是 data[288:576]。这样生成的 (input, output) 对保证了数据的时间连续性。
生成最终批次（Batch）数据：

2. 非预测channel的处理，包含history和future的数据

day和week的embedding

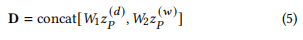
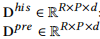
输入数据：从时间维度提取 [分钟索引, 星期几索引]。
将数据划分为 24 个 patch：288 划分成 24 * 12，每个 patch 包含 12 个时间步，但只选取每个 patch 中的第 1 个时间步。
Embedding 映射：将提取的时间信息映射到 128 维，其中 分钟 的 embedding 为 1441 x 128，星期几 的 embedding 为 8 x 128。
输出：
- x_th：表示过去时间的嵌入 (torch.Size([2, 24, 228, 256]))
- x_tp：表示未来时间的嵌入 (torch.Size([2, 24, 228, 256]))

spatial的特征

cal_lape 函数的主要目的是基于图的拉普拉斯矩阵生成空间特征嵌入，具体流程如下：

输入:
- adj_mx: 图的邻接矩阵，用于表示节点之间的连接关系。
步骤:
- 计算归一化拉普拉斯矩阵 L，并确定是否存在孤立节点。
- 对 L 进行 特征值分解，得到特征值 (EigVal) 和特征向量 (EigVec)。
- 根据特征值进行排序 (argsort)，以确保特征向量按特征值大小排列。
- 从排好序的特征向量中，选择 lape_dim（如 8 个）特征向量作为最终的嵌入表示，跳过孤立点对应的特征。
输出:
- 返回 laplacian_pe，即一个 EigVec 的子集，用作节点的空间嵌入特征。这些特征捕捉了图的拓扑结构信息。

空间维度的特征:

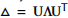
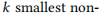
空间特征的处理方式完全不同，它基于压缩的邻接矩阵进行特征生成。
首先，使用拉普拉斯矩阵的特征向量（laplacian_pe）作为基础，通过 LaplacianPE 类将其输入到线性层 (nn.Linear)，从而将拉普拉斯特征向量映射到一个较高维度（如 256 维）。
线性变换: 这是一种通过矩阵运算将原始特征投影到一个高维连续空间的方式，而不是从预定义的字典中直接查找向量。
最终的输出空间嵌入是一个 (2, 24, 228, 256) 张量，通过 .repeat 操作复制并扩展以匹配批次和时间维度。

总结

时间特征: 是通过 embedding lookup 的方式，从预定义的字典中获取离散的时间标签的高维表示。类似于从词表中获取单词嵌入。
空间特征: 是基于 线性变换，通过拉普拉斯矩阵的特征向量，将其投影到高维空间。它是从图的结构中压缩和提取的特征，而非直接查找。

3. 预测channel的处理，包含history的数据

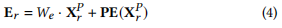
输入：x 的维度 (2, 228, 288)，表示 2 个批次，228 个空间站，288 个时间步。
时间步分割：将 288 时间步分成 24 个 patch，每个 patch 含 12 个时间步，得到 (2, 228, 24, 12)。
嵌入：
- Linear 处理：对每个 patch 的 12 个时间步使用 Linear 映射到 256 维，也就是 Linear 层将输入的 patch 从 (12,) 变为 (256,)。
- Position Encoding 处理：为每个 patch 加入位置编码 (PositionalEncoding)，这里的位置编码是基于 patch 在时间序列中的位置，即相同位置的 patch 在不同空间站间共享相同的 position_encoding。
输出：最终得到 (2, 24, 228, 256)，每个 patch 中 228 个空间站都有 256 维的嵌入表示。

4. 时间卷积核空间卷积模块

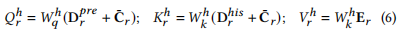
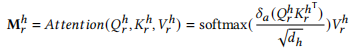
第二次注意力

残差 GCN

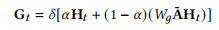
是的，在 st_attn 模块中，时间注意力机制的计算包括两次注意力运算和两次残差连接。具体步骤如下：

st_attn 模块主要通过时间上的注意力机制和空间特征的结合来进行特征学习。具体步骤如下：

输入说明:

x_q：输入的 query，来自 enc，维度为 (2, 24, 228, 256)，表示 2 个批次、24 个时间步、228 个空间站、256 维特征。
TH 和 TP：分别是历史和未来时间信息的嵌入，用于构造 key 和 query。

时间卷积和多头注意力:

首先对 TP 和 TH 进行线性变换，通过 tc_q_conv 和 tc_k_conv 获取 query 和 key，变换后的维度为 (2, 24, 228, 256)。
转置后得到 (2, 228, 24, 256)。
x_q 经过 tc_v_conv 得到 value，维度同样变为 (2, 228, 24, 256)。
将 query、key 和 value 通过 reshape 分解为多头注意力形式，得到 (2, 228, 16, 24, 16)，其中 tc_num_heads=16 和 head_dim=16。

时间注意力机制计算 - 第一次注意力运算:

计算时间上的注意力矩阵：tc_attn = (tc_q @ tc_k.transpose(-2, -1)) * self.scale，其中 self.scale=0.25，用来缩放防止梯度过大。维度为 (2, 228, 16, 24, 24)。这个步骤表示每个注意力头之间，不同时间步（patch）之间的关系计算。
通过 softmax 和 dropout 处理，得到加权后的 tc_attn。
利用 tc_attn @ tc_v 计算加权后的 value，得到 (2, 228, 16, 24, 16)。
通过 reshape 和 transpose 恢复为 (2, 24, 228, 256)，并与 x_q 相加，再经过 LlamaRMSNorm 归一化处理得到 tc_x。这一步形成了第一个残差连接，保留了原始输入 x_q 的信息。

时间注意力机制计算 - 第二次注意力运算:

对 tc_x 进行线性变换，获取新的 query、key 和 value，通过 t_q_conv、t_k_conv 和 t_v_conv 处理。
经过 reshape 和 permute 后，同样分解为多头注意力的形式 (2, 228, 16, 24, 16)。
计算新的注意力矩阵：t_attn = (t_q @ t_k.transpose(-2, -1)) * self.scale，经过 softmax 和 dropout 得到最终的注意力权重。
利用 t_attn @ t_v 得到加权后的输出 t_x，恢复维度后为 (2, 24, 228, 256)，再与 tc_x 相加，通过 LlamaRMSNorm 处理。这一步形成了第二个残差连接，保留了 tc_x 的信息。

空间特征结合:

将 t_x 送入 GCN，结合空间连接关系（adj），得到最终融合了时间和空间特征的 gcn_out，维度为 (2, 24, 228, 256)。

总结:

st_attn 通过两次时间上的注意力机制提取时序特征，每次都通过残差连接保留了输入的原始信息，同时结合 GCN 模块的空间特征，最终输出时空特征融合的结果。TH 和 TP 提供了时间嵌入，而 x_q 提供了流量特征嵌入，通过注意力机制融合在一起。

5. 转变为需要预测的维度

skip 的处理过程可以总结如下：

输入 enc：
- enc 的形状为 (2, 24, 228, 256)，表示 (batch_size, patches, nodes, embedding_dim)，其中 24 表示时间步长划分的 patch 数量，228 表示空间站的数量，256 是嵌入维度。
调整维度顺序：
- permute(0, 2, 3, 1) 将 enc 的维度从 (2, 24, 228, 256) 变为 (2, 228, 256, 24)，将 patches 维度移动到最后。调整后，每个空间站 (228) 有 256 维嵌入表示，这些表示来自于 24 个 patch。
展平操作：
- 使用 self.flatten（定义为 nn.Flatten(start_dim=-2)），将最后两个维度 (256 和 24) 展平成一个维度，得到 (2, 228, 6144)。其中 6144 = 256 * 24。
线性变换：
- 使用 self.linear，一个 Linear(in_features=6144, out_features=288, bias=True)，将 6144 维的输入变换为 288 维，得到 (2, 228, 288)。这一步的作用是将 24 个 patch 提取的嵌入表示整合为一个长度为 288 的特征。
调整维度顺序并添加新维度：
- transpose(1, 2) 将维度 1 和 2 交换，变成 (2, 288, 228)。这意味着现在每个时间步 (288) 有 228 个空间站的特征。
- unsqueeze(-1) 在最后添加一个新维度，得到 (2, 288, 228, 1)，为后续的预测做好准备。
截取时间步：
- skip = skip[:, :time_steps, :, :] 最终调整为 (2, 288, 228, 1)，确保 skip 的形状与时间步数相匹配，用于下一步预测。

6. 最后的forward

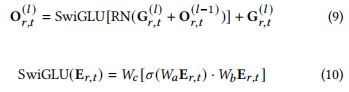
第一个O，实际上就是未归一化的x。self.mlp起到了SwiGLU的作用，self.norm2起到了RN的作用

if self.type_ln == 'pre':
    x_nor1 = self.norm1(x)  # 表示空间特征, torch.Size([2, 24, 228, 256]) -> torch.Size([2, 24, 228, 256])
    x = x + self.drop_path(self.st_attn(x_nor1, x_nor1, x_nor1, TH, TP, adj, geo_mask=geo_mask, sem_mask=sem_mask))  # 残差连接
    x = x + self.drop_path(self.mlp(self.norm2(x)))  # torch.Size([2, 24, 228, 256])

公式 (10):
$
SwiGLU(E_{r,t}) = W_c[\sigma(W_aE_{r,t}) \cdot W_bE_{r,t}]
$

公式描述了 SwiGLU 操作的细节，其中 $E_{r,t}$ 是经过线性变换的输入，通过 $σ$ 激活后，与另一线性变换的结果进行 Hadamard (逐元素) 乘积。
在代码中，self.mlp 实现了类似的操作：
```
return self.w2(F.silu(self.w1(x)) * self.w3(x))
```
- 这里 F.silu 相当于 σ 激活函数，self.w1(x) 和 self.w3(x) 进行线性变换后，通过逐元素乘积实现 SwiGLU。

7. 本文采用的归一化

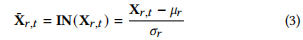
是的，LlamaRMSNorm 与 Layer Normalization 确实有相似之处，但它们之间有一些关键的区别：

1. 相似之处：

归一化目标：两者都是对特征向量（即 256 维度）进行归一化，以使得特征具有稳定的分布。这有助于在神经网络中提高训练的稳定性。
可学习的权重：两者在归一化后都会引入一个可学习的权重（self.weight），以确保归一化不会限制模型的表达能力。

2. 不同之处：

归一化计算方式：
- Layer Normalization：计算的是整个特征向量的 均值 (mean) 和 标准差 (std)，然后用公式 (x - mean) / std 来进行归一化。也就是说，它是计算均值和标准差，确保每个 (Batch, Patch, Node) 上的 256 维特征的均值为 0，标准差为 1。
  $ \text{LayerNorm}(x) = \frac{x - \text{mean}(x)}{\text{std}(x) + \epsilon} $
- RMS Normalization (RMSNorm)：只计算 均方根 (RMS)，然后用公式 x / RMS 来进行归一化。RMS 是特征平方的均值开方，确保特征的整体幅度一致，但不保证均值为 0。
  $ \text{RMSNorm}(x) = \frac{x}{\sqrt{\text{mean}(x^2)} + \epsilon} $
归一化效果：
- Layer Normalization：中心化并缩放，将输入特征拉到均值 0，标准差 1 的分布。
- RMS Normalization：只缩放，不改变均值，只调整特征的幅度，保留特征分布的形状。