5.4求解非凸非线性规划

fang--- / 2024-10-11 / 原文

import numpy as np
from scipy.optimize import minimize

# 定义目标函数
def objective(x):
    return -np.sum(np.sqrt(x))  # 注意：scipy的minimize默认是最小化问题，所以这里取负号

# 定义约束条件
constraints = [
    {'type': 'ineq', 'fun': lambda x: 10 - x[0]},  # x[0] <= 10
    {'type': 'ineq', 'fun': lambda x: 20 - (x[0] + 2 * x[1])},  # x[0] + 2*x[1] <= 20
    {'type': 'ineq', 'fun': lambda x: 30 - (x[0] + 2 * x[1] + 3 * x[2])},  # x[0] + 2*x[1] + 3*x[2] <= 30
    {'type': 'ineq', 'fun': lambda x: 40 - (x[0] + 2 * x[1] + 3 * x[2] + 4 * x[3])},  # x[0] + 2*x[1] + 3*x[2] + 4*x[3] <= 40
    {'type': 'ineq', 'fun': lambda x: 1000 - sum((100 - i) * x[i-1] for i in range(1, 101))}  # 加权求和小于等于1000
]

# 初始猜测值
x0 = np.zeros(100)

# 确保变量是非负的
bounds = [(0, None) for _ in range(100)]

# 调用minimize函数，并设置更大的迭代次数限制
options = {'maxiter': 1000}  # 增加迭代次数限制
result = minimize(objective, x0, method='SLSQP', bounds=bounds, constraints=constraints, options=options)

# 输出结果
if result.success:
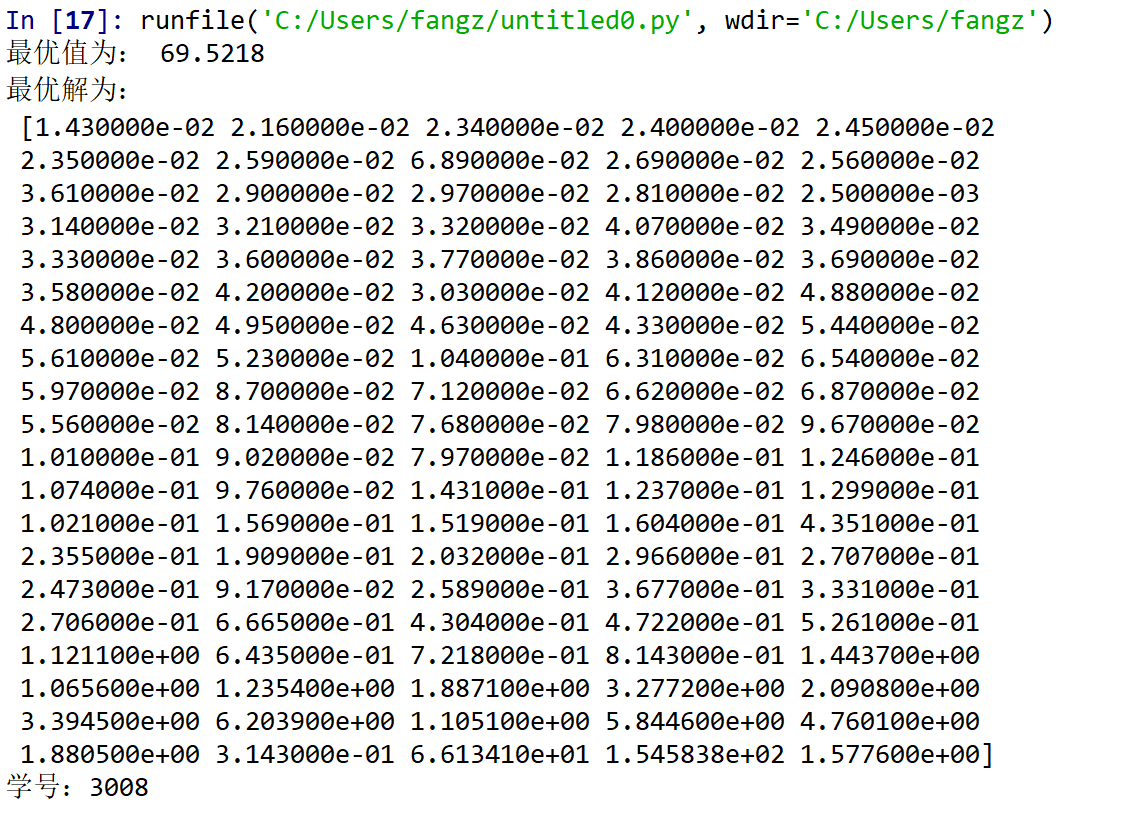
    print("最优值为：", -round(result.fun, 4))
    print("最优解为：\n", np.round(result.x, 4))
else:
    print("问题未找到最优解，状态为：", result.message)
print("学号：3008")

由于题目是非线性非凸规划问题，目标函数求最大化，我们转换成求最小化

导入库from scipy.optimize import minimize

结果如下