SciTech-Mathmatics-Probability+Statistics-VIII-Statistics:Quantifing Uncertainty+ANOCOVA(ANalysis of COVAriance)协方差分析原理

abaelhe / 2024-09-18 / 原文

SciTech-Mathmatics-Probability+Statistics-VIII-Statistics:Quantifing Uncertainty

ANOCOVA(ANalysis Of COVAriance)

协方差分析原理

ANOCOVA 是一种将RA(回归分析) 与 VA(方差分析) 结合的一种分析方法。
用来比较不同Samples的Means(均值), 同时控制一个或多个协变量(即可能影响结果的连续变量)的影响.

多组数据的比较可以用VA(方差分析), 但是如果不同Samples的Baseline本来就不一致,
直接分析测试结果数据, 直接用VA(方差分析)可能存在问题。
这时候就需要使用ANOCOVA(协方差分析)。

协方差分析基本思想是:

将不易控制的因素对因变量Y的影响看作是协变量X,
建立协变量X与因变量Y的 LR(线性回归)关系,
利用该LR(线性回归)关系将协变量X的值化为相等, 计算因变量Y的修正，
后对 因变量Y的修正 的均数进行比较。

ANOCOVA 的例子:

在研究不同教学方法对学生考试成绩的影响时,
学生的初始能力(比如之前的考试成绩)也会影响最终成绩。
为公平地比较不同教学方法的效果，要去除培训前成绩差异的影响。
研究对象分为两组接受不同治疗(如治疗组和安慰组),
每组分别在治疗前后测量观察指标(如血压值),
比较治疗前后的血压值时,需要去除不同研究对象本身血压值就有差异的影响。

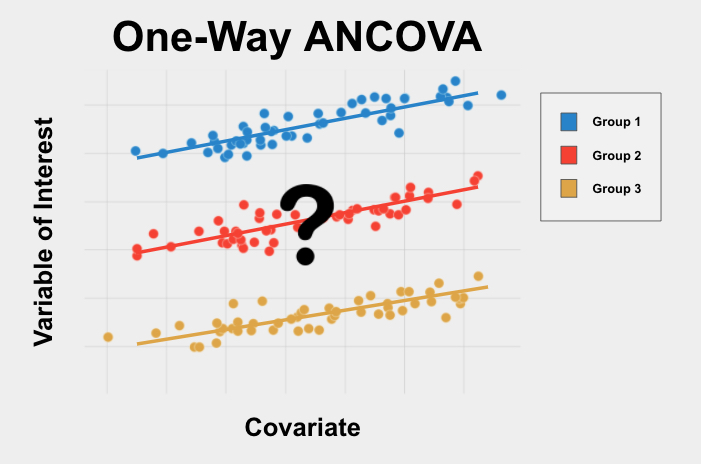
科学研究的ANOCOVA

来源：通过一个简单例子，通俗讲下协方差分析

临床经常碰到这种设计：研究对象分为两组, 接受不同治疗(如治疗组和安慰组)，
每组分别在治疗后前测量观察指标(如血压值). 目的是比较两种治疗方式是否有差异.
这种情况你会怎么处理呢？

我看过不少国内的文章，他们的做法有这么几种:

直接比较治疗后的两组指标，如血压值，用t检验比较；
先比较治疗前两组的差异，证明无统计学意义，然后再比较治疗后两组的差异；
先比较试验组治疗前和治疗后差异, 再比较对照组治疗前和治疗后差异，
如果试验组治疗后和治疗前差异更大，说明试验组更有效。

第 1. 种做法是肯定有问题的，因为它根本不考虑两组在疗前的差异。

为什么有问题呢？比方说，下面这个简单的例子：
有甲乙丙3个学生，期末考试成绩分别为90、85、80，
如果让你判断，你觉得哪个学生更优秀一些（只考虑成绩）？
当然，你可以毫不犹豫地说，甲最优秀，因为成绩最高。
但确实如此吗？再给你一组数据，
甲乙丙3个人的刚入学时的成绩，分别是95、85、60。
这时候谁更优秀呢？你可能要犹豫一下。
虽然甲的期末成绩最高，但是相比入学成绩而言，他是下降。
丙的期末成绩最低，可是相对入学成绩而言，他上升了很多。
作为老师，也许他不会评甲最优秀, 而是丙最优秀。因为成绩上升很快。
所以，很明显，我们是不应该只看治疗后两组差异的，这说明不了什么问题。

第 2. 种做法，比较好一些，起码通过统计学方法说明两组治疗前无统计学差异。
但是，统计学差异有时未必可靠，跟例数有关的.
如果例数少的话, 即使两组治疗前差别较大, 也是无统计学差异。
所以，也不是很好。

第 3. 种做法，听起来似乎也有理，但仔细想想。
试验组的治疗后前的差异比对照组的大, 是反映一种真实情况？还要统计学来证实的。
比如, 试验组的血压值治疗后前对比，降低2mmHg，对照组降低1.8mmHg,
仅从数字来看, 试验组降低更多, 但有意义？不一定。
比较两组差异的正确做法, 真正说明两组的差异，比较好的做法有两种:

倍差法(因为做了两次差值, 所以叫倍差法):
两组分别求出服药后前的血压值差值, 变成两组差值的比较, 用t检验或方差分析.
ANCOVA(协方差分析), 比较两组治疗后的血压值, 但以服药前血压值作为协变量, 校正其影响.
实际上是比较两组校正的服药后血压值。

第一种方法很简单, 只是一种思路而已, 仍然是t检验或方差分析, 不必多言。
第二种方法是协方差分析，本文主要介绍一下:

协方差分析的思想

大概就是：
把治疗前两组的数值作为一个协变量, 比较两组治疗后差异时, 校正这一协变量。
这样可以得到校正后的两组治疗后均值, 比较两组的校正均值。
比如说，a和b两组治疗后均值分别为62和56，
但是校正协变量后, 很可能就变成了59和59,
这时比较两个校正均值59和59，两组就没有统计学差异。

基本概念: 协变量、因变量、自变量

Dependent Variable(因变量)
因变量是研究时被测量的结果或反应变量。
比如研究教学方法对学生成绩影响时，因变量是不同的研究教学方法。
Independent Variable(自变量)
自变量是研究时被操纵或分类的变量，用于探讨其对因变量的影响。
比如研究教学方法对学生成绩影响时，自变量是学生之后的成绩。
Covariate(协变量)
协变量是那些可能影响因变量的变量，但不是主要研究对象。
通过控制这些变量, 可以更准确地评估自变量对因变量的影响。
比如研究教学方法对学生成绩影响时，协变量是学生之前的成绩。

主效应和交互效应

主效应：
自变量对因变量的直接影响, 不考虑协变量。
交互效应：
自变量和协变量之间的交互作用对因变量的影响,
要求
1. 所关注的变量应该是连续的、正态分布的，各组方差齐性。
  各组应该是独立的（互不相关），
  并且应该有足够的数据（每组有 5 个以上的值）。
2. 因变量与协变量之间的回归关系必须是线性的。
3. 自变量与因变量之间没有交互作用。
  交互作用也可以认为代表斜率, 没有显著作用，说明斜率不存在显著差异。只有当分类变量和连续变量之间没有显著的交互作用，才可以进行ANCOVA。

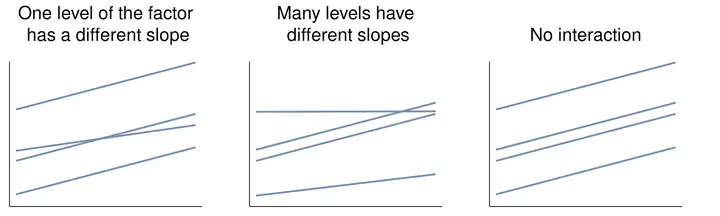
以协变量为x轴，以因变量为y轴，
如果交互作用显著，则会出现类似左图和中图的情况。

分析策略

如果 只有组别变量显著, 则放弃协变量。 从模型删除变量，
这时得到一个方差分析。
如果 只有协变量显著, 则放弃组别变量。 从模型提取一个变量，
这时得到一个简单的LR(线性回归)结果.
如果 交互作用显著，即协变量对因变量的影响因组别的不同而不同.
此时, 需要考虑交互作用对因变量的影响。可以对不同组别分别进行RA(回归分析),
以更深入地了解协变量在不同组别的效应。

绘制三个Figure

ANOCOVA Prediction Plot：
绘制三组协变量和因变量的相关性，并进行回归。
可以简单查看协变量和因变量是否成线性相关关系，
若不成立，则不能进行ANOCOVA分析
ANOCOVA Coefficients:
展示三组回归的系数
ANOCOVA Test Results:
展示自变量、协变量和自变量与协变量相互作用对因变量的影响，
如果相互作用的p-value<0.05，则说明三组斜率显著不一，
则不能进行ANOCOVA分析
ANOCOVA Test Results的结果其实等效于:
线性回归模型 FinalScore ~ InitialScore * Method

问题

协方差分析为什么要看协变量和组别的相互作用
ANOCOVA假设协变量和因变量之间的关系在所有Samples(组别)是一致的。
如果协变量在Samples(组别)之间存在显著的相互作用，
这表示协变量对因变量的影响在不同Samples(组别)之间是不一致的。
如何理解 "ANOCOVA建立协变量X与因变量Y的LR(线性回归)关系，
利用该回归关系将协变量X的值化为相等，
计算因变量Y的修正均值，
再对因变量Y的修正均数进行比较。"
这句话可以看下图:

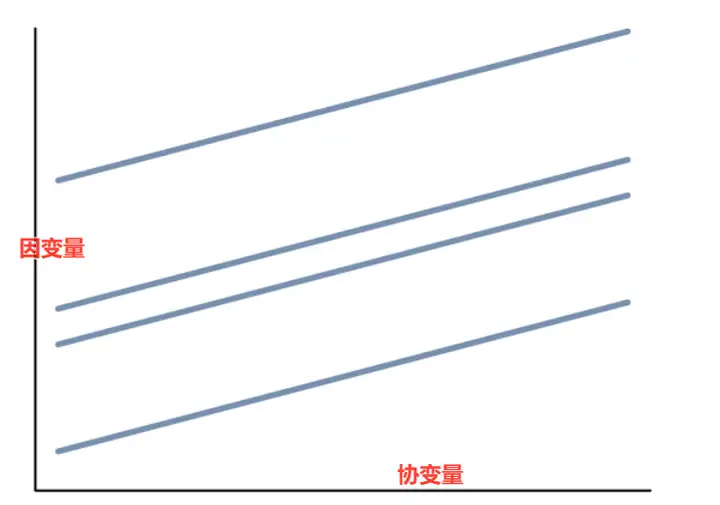
ANOCOVA是 协变量为x轴，因变量为y轴，对Samples(各组)RA(回归分析),
看Samples(各组)因变量随着协变量的变化是否有显著差异。
从上图看到, 当Samples(各组)协变量通过回归都相等时, 各组因变量值的差异,
从而计算显著差异。
❓但是"说计算因变量Y的修正的均值", 我没有搞懂是怎么计算修正均值的？
是直接LR(线性回归)模型套ANOVA就可以计算均值并计算显著性？

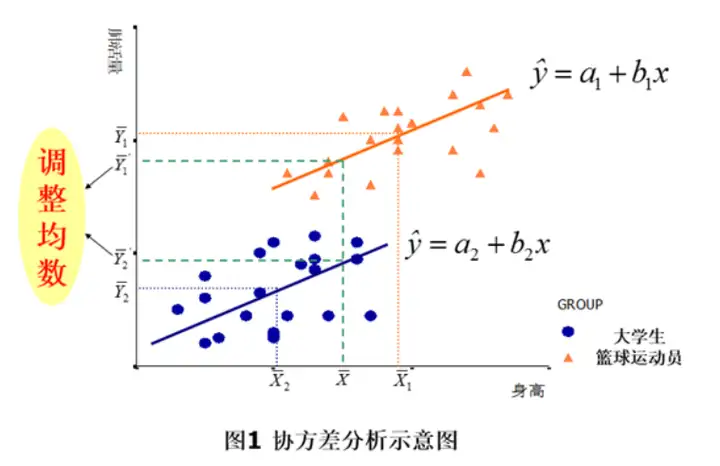
调整均数是对Samples(各组)求协变量的均值，然后得到一个总协变量均值，
根据回归关系，得到各组的调整均值公式：
$\large \overset{-'}{y_{i}} = \overset{-}{y_i}− \beta_{yx(e)} (\overset{-}{x_i}−\overset{-}{x})$
❓那么是怎么根据校正均值进行方差分析的？
暂时不管了