11_乘最多水的容器

【问题描述】

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。说明：你不能倾斜容器。

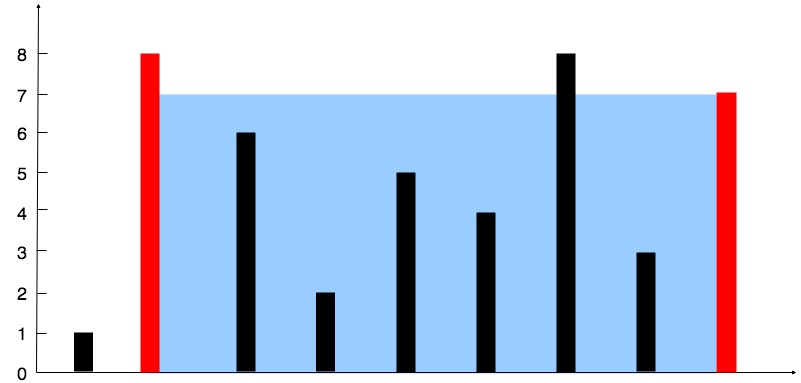
示例一：
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例二：
输入：height = [1,1]
输出：1

【算法设计思想】

在解决本题时，笔者首先使用了较为常见的暴力解法，即遍历一遍数组，但是当数据一大就会超出了时间的限制，暴力解法的时间复杂度达到了O(n^2)，其效率是极其低下的。（原谅我是一个笨比😇。)
暴力解法的C++描述如下：

class Solution {
public:
    int maxArea(vector<int>& height) {
        int n = height.size();
        int answer = 0;
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                int width = j - i;
                int minHeight = height[i] < height[j] ? height[i] : height[j];
                answer = answer < width * minHeight ? (width * minHeight) : answer;
            }
        }
        return answer;
    }
};

好了，接下来让我们步入正轨，开始讲解正确的解法：
本题分治法，动态规划都不适用，要想得到O（n）的时间复杂度，只能够使用双指针法。这里我们要注重缩减搜索空间这个思想。关键的思路在于，每次我们移动较短的那根柱子。（有点贪心的味道在其中了。）

【算法描述】

C++：

class Solution {
public:
    int maxArea(vector<int>& height) {
        int result = 0;
        int i = 0;
        int j = height.size() - 1;
        while(i < j){
            int area = (j - i) * min(height[i],height[j]);
            result = max(area,result);
            if(height[i] < height[j]){
                i++;
            }else{
                j--;
            }
        }
        return result;
    }
};

Java：

class Solution {
    public int maxArea(int[] height) {
        int len = height.length;
        int i = 0;
        int j = len - 1;
        int area = 0;
        int result = 0;
        while(i < j){
            int minHeight = Math.min(height[i],height[j]);
            area = (j - i) * minHeight;
            result = Math.max(area,result);
            if(height[i] < height[j]){
                ++i;
            }else{
                --j;
            }
        }
    return result;
    }
}

Python：

class Solution:
    def maxArea(self, height: List[int]) -> int:
        size = len(height)
        area = 0
        result = 0
        i = 0
        j = size - 1
        while i < j:
            area = (j - i) * min(height[i],height[j])
            result = max(result,area)
            if(height[i] < height[j]):
                i = i + 1
            else:
                j = j - 1
        return result         

C语言：

int maxArea(int* height, int heightSize) {
    int area = 0;
    int result = 0;
    int i = 0;
    int j = heightSize - 1;
    while(i < j){
        int minHeight = height[i] < height[j] ? height[i] : height[j];
        area = (j - i) * minHeight;
        result = result < area ? area : result;
        if(height[i] < height[j]){
            i++;
        }else{
            j--;
        }
    }
    return result;
}