[Leetcode]经典算法
检测环
快慢指针法是一种用于检测链表中是否存在环的有效方法,同时也可以找到环的起点。该方法的原理基于两个指针在链表上同时移动,其中一个移动得更快,而另一个移动得更慢。
-
检测环的存在:
- 使用两个指针,一个称为快指针(fast),一个称为慢指针(slow)。
- 在每一步中,快指针向前移动两步,而慢指针只移动一步。
- 如果链表中不存在环,那么快指针最终会到达链表的尾部,此时可以确定链表中无环。
- 如果链表中存在环,由于快指针的速度比慢指针快,它们最终会相遇。
-
找到环的起点:
- 一旦快慢指针相遇,说明链表中存在环。
- 将其中一个指针(例如慢指针)重新移到链表的头部,保持另一个指针在相遇点。
- 然后,两个指针以相同的速度前进,直到它们再次相遇。这次相遇点就是环的起点。
为什么这个方法有效?
- 如果链表中不存在环,快指针将最终到达链表的尾部,而慢指针也会到达链表的末尾。由于没有环,两者不会相遇。
- 如果链表中存在环,快慢指针最终会在环中的某一点相遇。此时,将其中一个指针移到链表头部,它们再次相遇的地方就是环的起点。
这个方法的时间复杂度为O(N),其中N是链表的长度。因为快指针每次移动两步,而慢指针每次移动一步,所以快指针最多需要N/2步就能遇到慢指针。在找到相遇点后,重新移动指针的过程最多需要再走N步。
证明
让我们来证明一下,为什么上面两个说法是正确的。
首先,进入环之前的路越长,快慢指针之间的差距就越大,如果这段路足够长,甚至会出现快指针已经在环里面走了好几圈,但是慢指针还没有进入环的情况。
但是不管前面的路有多长,不管慢指针进入环的时候,快指针在环的哪个位置,慢指针进入环以后,快指针总是可以在慢指针走不到一圈的时候追上他,因为慢指针在环内走了一圈的时候,快指针已经走了两圈,一定可以追得上。
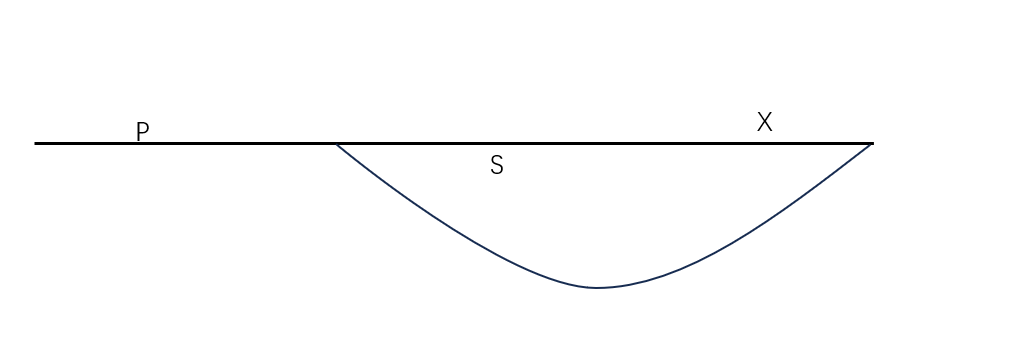
下面我们来列算式
进入环之前的路长度为:P
慢节点在环内走过的路为:S
环的总长度为:C
慢指针总共走过的长度:P+S
那么快指针走过的总长度:2(P+S)
快指针在环内走过的长度:P+2S
快慢指针相遇的时候,他们处在同一个位置上:S%C = (P+2S)%C
化简,(P+S)%C = 0,也就是说(P+S) = NC
现在我们在位置S上,再走P的长度就可以回到环的起点。
先来看如何判断是否有环
Leetcode 141. 环形链表
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ,则返回 true 。 否则,返回 false 。
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def hasCycle(self, head: Optional[ListNode]) -> bool:
if not head:
return False
fast = head
slow = head
while fast.next and fast.next.next:
fast = fast.next.next
slow = slow.next
if fast == slow:
return True
return False
再来看环的起点在哪里
LCR 022. 环形链表 II
给定一个链表,返回链表开始入环的第一个节点。 从链表的头节点开始沿着 next 指针进入环的第一个节点为环的入口节点。如果链表无环,则返回 null。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。注意,pos 仅仅是用于标识环的情况,并不会作为参数传递到函数中。
说明:不允许修改给定的链表。
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def detectCycle(self, head: ListNode) -> ListNode:
if not head:
return False
fast = head
slow = head
while fast.next and fast.next.next:
fast = fast.next.next
slow = slow.next
if fast == slow:
fast = head
while fast != slow:
fast = fast.next
slow = slow.next
return fast
return False
TOP K
问题描述:
从arr[1, n]这n个数中,找出最大的k个数,这就是经典的TopK问题。
栗子:
从arr[1, 12]={5,3,7,1,8,2,9,4,7,2,6,6} 这n=12个数中,找出最大的k=5个。
整体排序
排序是最容易想到的方法,将n个数排序之后,取出最大的k个,即为所得。
伪代码:
sort(arr, 1, n);
return arr[1, k];
时间复杂度:O(n*lg(n))
分析:明明只需要TopK,却将全局都排序了,这也是这个方法复杂度非常高的原因。那能不能不全局排序,而只局部排序呢?这就引出了第二个优化方法。
局部排序
不再全局排序,只对最大的k个排序。
冒泡是一个很常见的排序方法,每冒一个泡,找出最大值,冒k个泡,就得到TopK。
伪代码:
for(i=1 to k){
bubble_find_max(arr,i);
}
return arr[1, k];
时间复杂度:O(n*k)
分析:冒泡,将全局排序优化为了局部排序,非TopK的元素是不需要排序的,节省了计算资源。不少朋友会想到,需求是TopK,是不是这最大的k个元素也不需要排序呢?这就引出了第三个优化方法。
堆
思路:只找到TopK,不排序TopK。
先用前k个元素生成一个小顶堆,这个小顶堆用于存储,当前最大的k个元素。
接着,从第k+1个元素开始扫描,和堆顶(堆中最小的元素)比较,如果被扫描的元素大于堆顶,则替换堆顶的元素,并调整堆,以保证堆内的k个元素,总是当前最大的k个元素。
直到,扫描完所有n-k个元素,最终堆中的k个元素,就是求的TopK。
import heapq
nums = [1, 4, 7, 8, 5, 2, 3, 6, 9]
k = 3
heap = nums[:k]
heapq.heapify(heap)
for i in nums[k:]:
if i > heap[0]:
heapq.heappop(heap)
heapq.heappush(heap, i)
print(heap)
时间复杂度:O(n*lg(k))
画外音:n个元素扫一遍,假设运气很差,每次都入堆调整,调整时间复杂度为堆的高度,即lg(k),故整体时间复杂度是n*lg(k)。
分析:堆,将冒泡的TopK排序优化为了TopK不排序,节省了计算资源。堆,是求TopK的经典算法,那还有没有更快的方案呢?
随机选择
随机选择算在是《算法导论》中一个经典的算法,其时间复杂度为O(n),是一个线性复杂度的方法。
这个方法并不是所有同学都知道,为了将算法讲透,先聊一些前序知识,一个所有程序员都应该烂熟于胸的经典算法:快速排序。
其伪代码是:
void quick_sort(int[]arr, int low, int high){
if(low==high) return;
int i = partition(arr, low, high);
quick_sort(arr, low, i-1);
quick_sort(arr, i+1, high);
}
其核心算法思想是,分治法。
分治法(Divide&Conquer),把一个大的问题,转化为若干个子问题(Divide),每个子问题“都”解决,大的问题便随之解决(Conquer)。这里的关键词是“都”。从伪代码里可以看到,快速排序递归时,先通过partition把数组分隔为两个部分,两个部分“都”要再次递归。
分治法有一个特例,叫减治法。
减治法(Reduce&Conquer),把一个大的问题,转化为若干个子问题(Reduce),这些子问题中“只”解决一个,大的问题便随之解决(Conquer)。这里的关键词是“只”。
二分查找binary_search,BS,是一个典型的运用减治法思想的算法,其伪代码是:
int BS(int[]arr, int low, inthigh, int target){
if(low> high) return -1;
mid= (low+high)/2;
if(arr[mid]== target) return mid;
if(arr[mid]> target)
return BS(arr, low, mid-1, target);
else
return BS(arr, mid+1, high, target);
}
从伪代码可以看到,二分查找,一个大的问题,可以用一个mid元素,分成左半区,右半区两个子问题。而左右两个子问题,只需要解决其中一个,递归一次,就能够解决二分查找全局的问题。
通过分治法与减治法的描述,可以发现,分治法的复杂度一般来说是大于减治法的:
快速排序:O(n*lg(n))
二分查找:O(lg(n))
话题收回来,快速排序的核心是:
i = partition(arr, low, high);
这个partition是干嘛的呢?
顾名思义,partition会把整体分为两个部分。
更具体的,会用数组arr中的一个元素(默认是第一个元素t=arr[low])为划分依据,将数据arr[low, high]划分成左右两个子数组:
左半部分,都比t大
右半部分,都比t小
中间位置i是划分元素
以上述TopK的数组为例,先用第一个元素t=arr[low]为划分依据,扫描一遍数组,把数组分成了两个半区:
左半区比t大
右半区比t小
中间是t
partition返回的是t最终的位置i。
很容易知道,partition的时间复杂度是O(n)。
画外音:把整个数组扫一遍,比t大的放左边,比t小的放右边,最后t放在中间N[i]。
partition和TopK问题有什么关系呢?
TopK是希望求出arr[1,n]中最大的k个数,那如果找到了第k大的数,做一次partition,不就一次性找到最大的k个数了么?
画外音:即partition后左半区的k个数。
问题变成了arr[1, n]中找到第k大的数。
再回过头来看看第一次partition,划分之后:
i = partition(arr, 1, n);
如果i大于k,则说明arr[i]左边的元素都大于k,于是只递归arr[1, i-1]里第k大的元素即可;
如果i小于k,则说明说明第k大的元素在arr[i]的右边,于是只递归arr[i+1, n]里第k-i大的元素即可;
这就是随机选择算法randomized_select,RS,其伪代码如下:
int RS(arr, low, high, k){
if(low== high) return arr[low];
i= partition(arr, low, high);
temp= i-low; //数组前半部分元素个数
if(temp>=k)
return RS(arr, low, i-1, k); //求前半部分第k大
else
return RS(arr, i+1, high, k-i); //求后半部分第k-i大
}
现在来看TOPK例题
Leetcode 面试题 17.14. 最小K个数
设计一个算法,找出数组中最小的k个数。以任意顺序返回这k个数均可。
给出python实现
class Solution:
def smallestK(self, arr: List[int], k: int) -> List[int]:
def top(arr,k):
left,mid,right = partition(arr)
left_length = len(left)
mid_length = len(mid)
if left_length >= k:
return top(left,k)
elif k>left_length and k<= left_length+mid_length:
return left + mid[:k-left_length]
elif k>left_length + mid_length:
return left+mid+top(right,k-left_length-mid_length)
def partition(arr):
if not arr:
return [],[],[]
select = random.choice(arr)
left,mid,right = [],[],[]
for value in arr:
if value < select:
left.append(value)
elif value == select:
mid.append(value)
elif value > select:
right.append(value)
return left,mid,right
if k == 0:
return []
return top(arr,k)
现在来看第K个数
Leetcode LCR 076. 数组中的第 K 个最大元素
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
class Solution:
def findKthLargest(self, nums: List[int], k: int) -> int:
def topK(nums, k):
left, mid, right = partition(nums)
left_length = len(left)
mid_length = len(mid)
right_length = len(right)
if right_length >= k:
return topK(right, k)
elif k > right_length and k <= right_length + mid_length:
return mid[0]
elif k > right_length + mid_length:
return topK(left, k - right_length - mid_length)
def partition(arr):
if not arr:
return [], [], []
select = random.choice(arr)
left,mid,right = [],[],[]
for n in arr:
if n < select:
left.append(n)
elif n == select:
mid.append(n)
elif n > select:
right.append(n)
return left, mid, right
return topK(nums,k)
再次强调一下:
分治法,大问题分解为小问题,小问题都要递归各个分支,例如:快速排序
减治法,大问题分解为小问题,小问题只要递归一个分支,例如:二分查找,随机选择
通过随机选择(randomized_select),找到arr[1, n]中第k大的数,再进行一次partition,就能得到TopK的结果。
总结
-
TopK,不难;其思路优化过程,不简单
-
全局排序,O(n*lg(n))
-
局部排序,只排序TopK个数,O(n*k)
-
堆,TopK个数也不排序了,O(n*lg(k))
-
分治法,每个分支“都要”递归,例如:快速排序,O(n*lg(n))
-
减治法,“只要”递归一个分支,例如:二分查找O(lg(n)),随机选择O(n)
-
TopK的另一个解法:随机选择+partition
算法
字节经典题目:小于n的最大数
给定一个数n和一个数组nums,用数组中的数字组合出小于n的最大数(可重复使用)
用了贪心+dfs,写的不太好
合并k个有序数组
二分法
二分法的几个位置
比如
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 3 | 3 | 3 | 3 | 4 | 5 | 6 |
有时候想要寻找小于3的最大数字
有时候想要寻找第一个满足>=3的数字,
有时候想要寻找最后一个满足>=3的数字,
有时候想要寻找小于4的最大数字
nums = [1, 2, 3, 4, 5, 5, 5, 5, 5, 6, 7, 8, 9]
n = len(nums)
left = 0
right = n - 1
result = -1
target = 5
while left <= right:
mid = (left + right) // 2
if nums[mid] < target:
result = mid
left = mid + 1
else:
right = mid - 1
print(result, nums[result])
left = 0
right = n - 1
result = -1
target = 5
while left <= right:
mid = (left + right) // 2
if nums[mid] > target:
result = mid
right = mid - 1
else:
left = mid + 1
print(result, nums[result])
left = 0
right = n - 1
result = -1
target = 5
while left <= right:
mid = (left + right) // 2
if nums[mid] == target:
result = mid
right = mid - 1
elif nums[mid] > target:
right = mid - 1
else:
left = mid + 1
print(result, nums[result])
left = 0
right = n - 1
result = -1
target = 5
while left <= right:
mid = (left + right) // 2
if nums[mid] == target:
result = mid
left = mid + 1
elif nums[mid] > target:
right = mid - 1
else:
left = mid + 1
print(result, nums[result])
遍历
深度优先遍历
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
node1 = TreeNode(1)
node2 = TreeNode(2)
node3 = TreeNode(3)
node4 = TreeNode(4)
node5 = TreeNode(5)
node6 = TreeNode(6)
node7 = TreeNode(7)
node1.left = node2
node1.right = node5
node2.left = node3
node2.right = node4
node5.left = node6
node5.right = node7
root = node1
def pre_order(root):
if root:
print(root.val, end=' ')
pre_order(root.left)
pre_order(root.right)
pre_order(root)
print()
def in_order(root):
if root:
in_order(root.left)
print(root.val, end=' ')
in_order(root.right)
in_order(root)
print()
def post_order(root):
if root:
post_order(root.left)
post_order(root.right)
print(root.val, end=' ')
post_order(root)