预测算法-20230801(持续更新)
第一章-关于预测的核心算法
-
机器学习中的预测算法,本笔记主要记录“函数逼近”问题下的预测。属于监督学习的一种
-
函数逼近常见算法:线性回归、逻辑回归
-
应用:分类问题、回归问题
-
函数逼近的主要分类:惩罚线性回归、集成方法
- 大、小数据集,宽、高瘦数据集
- 宽数据:每次观测有大量的测量项,但是观测次数有限,列数很多,行有限
- 高瘦数据:列有限,行很多
-
预测属性的数目,正确案例的百分比
- 样本的平衡性
- 提升决策树、随机森林、投票决策树、逻辑回归
- 支持向量机、K最邻进、人工神经网络
-
惩罚性线性回归
- 惩罚性线性回归可以减少样本数量使之与数据规模、问题复杂度相匹配。可以处理大量的特征
- 如果数据包含大量特征,但是训练时间和规模较小,惩罚回归法优于其余方法。
- 逻辑回归适用于大规模数据集
- 惩罚性线性回归的训练时间快,预测时间也快,可用于高速交易、互联网广告的植入等。
- 特征提取:明确每个特征对预测结果的重要性,根据对预测结果的贡献程度对特征打分。
-
集成方法
- 基本思想是构建多个不同的预测模型,然后将其输出做某种组合作为最终的输出,采用平均值或者采用多数人的投票。
- 单个预测模型为基学习器,只需结果优于基学习器即可
预测模型构建
- 提炼问题模型
- 算法步骤
- 预测模型的构建
- 选取用于预测的特征
- 设定训练目标
- 面向部署的算法性能评估
注意事项:
预测算法:包括有无记忆效应的预测方法。
- 模型的自由度必须要小于数据点的个数。
- 需要反复迭代确定最优的特征选取方案
- 可以采用将数据分类,分别采用不同的预测方法。
- 需要寻找关于实际问题领域的关键特征指标,需要参考文献来给出,比如证券价格领域的RSI\MACD指标。
- 模型简单-性能不好,模型复杂-过拟合
机器学习问题:
- 问题重构
- 问题的定性描述
- 问题的数学描述
- 模型训练与性能评估
- 再次修正问题重构
- 模型部署
第二章-通过数据了解问题
- 特征:数值、类型形式
- 惩罚性算法只能处理数值形式的特征
- 类型变量可以转为数值变量
- 属性和标签均既可以为类型形式的变量
- 标签=数值类型,回归问题;标签=类型形式,分类问题。
- 分类问题比回归问题简单,且可以相互转换。
数据集检查:
-
行列数
-
类别变量的数目、类别的取值范围
-
缺失值(可以平均值插值)
-
属性和标签的统计特性
-
免费数据库:UCI机器学习数据库
实例:分类问题-用声纳发现未爆炸的水雷
分辨岩石和水雷
- 1确定数据规模
- 2确定每个属性的特征
- 确定数值类型,把定性指标改为定量指标
- 3数值型和类别型属性的统计信息
__author__ = 'mike_bowles'
import urllib.request, urllib.error, urllib.parse
import sys
import numpy as np
#read data from uci data repository
target_url = ("https://archive.ics.uci.edu/ml/machine-learning-"
"databases/undocumented/connectionist-bench/sonar/sonar.all-data")
data = urllib.request.urlopen(target_url)
#arrange data into list for labels and list of lists for attributes
xList = []
labels = []
for line in data:
#split on comma
row = line.strip().decode().split(",")
xList.append(row)
nrow = len(xList)
ncol = len(xList[1])
type = [0]*3
colCounts = []
#generate summary statistics for column 3 (e.g.)
col = 3
colData = []
for row in xList:
colData.append(float(row[col]))#读取第三列数据
colArray = np.array(colData)#列表转数组
#数组底层使用C程序编写,运算速度快,使用对列表进行循环的方式来创建新列表
#数组元素要求是相同类型,而列表的元素可以是不同类型。
colMean = np.mean(colArray)#求平均值
colsd = np.std(colArray)#求方差
sys.stdout.write("Mean = " + '\t' + str(colMean) + '\t\t' +
"Standard Deviation = " + '\t ' + str(colsd) + "\n")
#calculate quantile boundaries
ntiles = 4
#计算四分位数边界
percentBdry = []
for i in range(ntiles+1):
percentBdry.append(np.percentile(colArray, i*(100)/ntiles))
#0,25,50,75,100
sys.stdout.write("\nBoundaries for 4 Equal Percentiles \n")
print(percentBdry)
sys.stdout.write(" \n")
#run again with 10 equal intervals
ntiles = 10
#10分位数
percentBdry = []
for i in range(ntiles+1):
percentBdry.append(np.percentile(colArray, i*(100)/ntiles))
sys.stdout.write("Boundaries for 10 Equal Percentiles \n")
print(percentBdry)
sys.stdout.write(" \n")
#最后一列包含分类变量
col = 60
colData = []
for row in xList:
colData.append(row[col])#选取第61列
unique = set(colData)
sys.stdout.write("Unique Label Values \n")
print(unique)
#计算具有每个值的元素的个数
catDict = dict(zip(list(unique),range(len(unique))))#数据格式:字符串类别=数值型类别(0,1,)
catCount = [0]*2#只有2个类别,所以用二维的计数
#elt=‘M’,catDict[‘M’]=1,catDict[‘R’]=2
for elt in colData:
catCount[catDict[elt]] += 1
sys.stdout.write("\nCounts for Each Value of Categorical Label \n")
print(list(unique))#列表unique的类别值
print(catCount)#计数向量
* 描述性统计(数值型)、数量分布(类别型)
* 读取某一列,计算均值和方差
- 4用分位数图展示异常点
__author__ = 'ubuntu'
##QQ分位图绘制
#Q-Q 图是通过比较数据和正态分布的分位数是否相等来判断数据是不是符合正态分布
# 也可以判断2列不同的数据是否符合同一个分布
#QQ图可以判断数据是服从卡方分布还是T分布等等
import numpy as np
import pylab
import scipy.stats as stats
import urllib.request, urllib.error, urllib.parse
import matplotlib.pyplot as plt
import sys
target_url = ("https://archive.ics.uci.edu/ml/machine-learning-"
"databases/undocumented/connectionist-bench/sonar/sonar.all-data")
data = urllib.request.urlopen(target_url)
#arrange data into list for labels and list of lists for attributes
xList = []
labels = []
for line in data:
#split on comma
#实验数据由逗号分割,所以对数据集用逗号分割读入数据
row = line.strip().decode().split(",")#读取行数据
xList.append(row)
nrow = len(xList)
ncol = len(xList[1])
type = [0]*3
colCounts = []
#图1
col = 3
colData = []
for row in xList:
colData.append(float(row[col]))#读取第三列的所有数据
fig1 = plt.figure()
sss4=stats.probplot(colData, dist="norm", plot=pylab)#绘制与正态分布差距的QQ图
pylab.show()
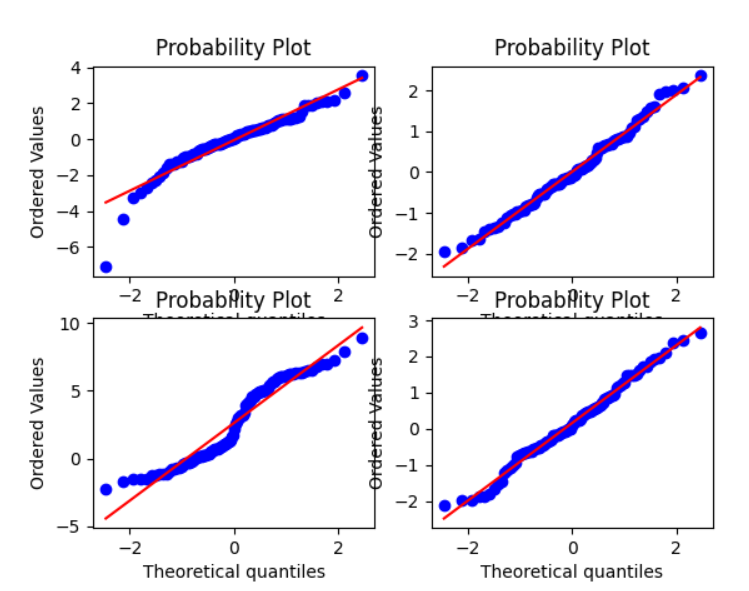
#图2
nsample = 100
rng = np.random.default_rng()
#具有小自由度的 t 分布:
ax1 = plt.subplot(221)
x = stats.t.rvs(3, size=nsample, random_state=rng)
res = stats.probplot(x, plot=plt)
#具有较大自由度的 t 分布:
ax2 = plt.subplot(222)
x = stats.t.rvs(25, size=nsample, random_state=rng)
res = stats.probplot(x, plot=plt)
#两个正态分布与广播的混合:
ax3 = plt.subplot(223)
x = stats.norm.rvs(loc=[0,5], scale=[1,1.5],
size=(nsample//2,2), random_state=rng).ravel()
res = stats.probplot(x, plot=plt)
#标准正态分布:
ax4 = plt.subplot(224)
x = stats.norm.rvs(loc=0, scale=1, size=nsample, random_state=rng)
res = stats.probplot(x, plot=plt)
#使用 dist 和 sparams 关键字生成具有对数伽玛分布的新图形:
#图3
fig2 = plt.figure()
ax = fig2.add_subplot(111)
x = stats.loggamma.rvs(c=2.5, size=500, random_state=rng)
res = stats.probplot(x, dist=stats.loggamma, sparams=(2.5,), plot=ax)
ax.set_title("Probplot for loggamma dist with shape parameter 2.5")
#使用 Matplotlib 显示结果:
plt.show()
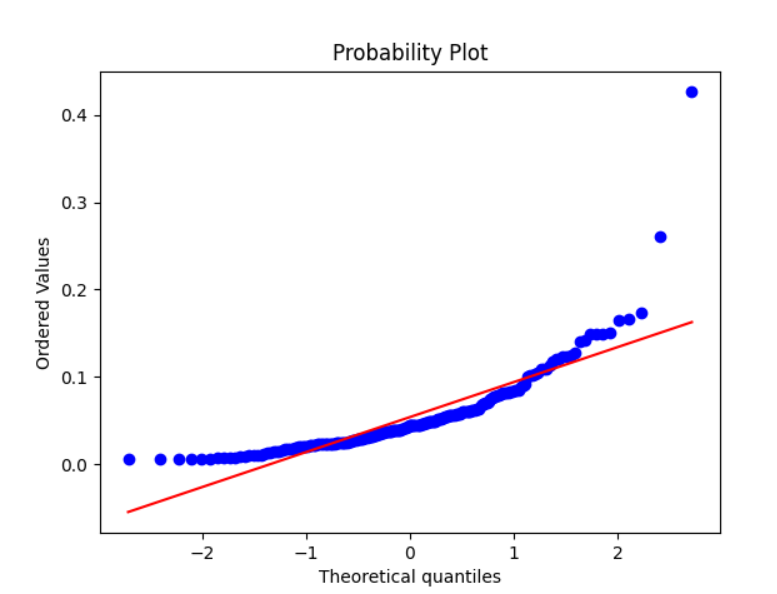
* 找到异常值和缺失值
* 四分位数图-可视化确定缺失值
* Q-Q 图是通过比较数据和正态分布的**分位数**是否相等来判断数据是不是符合正态分布,也可以判断2列不同的数据是否符合同一个分布
* QQ图可以判断数据是服从卡方分布还是T分布等等
- 5类别属性的统计特征
- 随机森林最多支持32类别,可以采用分层抽样法,合并和减少类别
- 6利用pandas对数据进行统计分析
__author__ = 'mike_bowles'
import pandas as pd
from pandas import DataFrame
import matplotlib.pyplot as plot
target_url = ("https://archive.ics.uci.edu/ml/machine-learning-"
"databases/undocumented/connectionist-bench/sonar/sonar.all-data")
#read rocks versus mines data into pandas data frame
rocksVMines = pd.read_csv(target_url,header=None, prefix="V")
#print head and tail of data frame
#数据名.head( ) :是指取数据的前n行数据,默认是前5行。
#需要注意的是没有print语句,python中的head()函数只是选择数据,而不对数据内容做任何改变。
print(rocksVMines.head())
#tail()调用者对象的最后 n 行,默认为后5行
print(rocksVMines.tail())
#print summary of data frame
#调用此处命令的时候,可能matplotlib和pands以及numpy版本存在版本不兼容,会报错,需要更新版本
summary = rocksVMines.describe()
print(summary)
#pandas有两个核心数据结构 Series和DataFrame,分别对应了一维的序列和二维的表结构。
#而describe()函数就是返回这两个核心数据结构的统计变量。其目的在于观察这一系列数据的范围、大小、波动趋势等等
#为后面的模型选择打下基础
#输出结果(不包含第60列的类别型数据)
# [5 rows x 61 columns]
# V0 V1 V2 V3 V4 V5 \
# count 208.000000 208.000000 208.000000 208.000000 208.000000 208.000000
# mean 0.029164 0.038437 0.043832 0.053892 0.075202 0.104570
# std 0.022991 0.032960 0.038428 0.046528 0.055552 0.059105
# min 0.001500 0.000600 0.001500 0.005800 0.006700 0.010200
# 25% 0.013350 0.016450 0.018950 0.024375 0.038050 0.067025
# 50% 0.022800 0.030800 0.034300 0.044050 0.062500 0.092150
# 75% 0.035550 0.047950 0.057950 0.064500 0.100275 0.134125
# max 0.137100 0.233900 0.305900 0.426400 0.401000 0.382300
#
# V6 V7 V8 V9 ... V50 \
# count 208.000000 208.000000 208.000000 208.000000 ... 208.000000
# mean 0.121747 0.134799 0.178003 0.208259 ... 0.016069
# std 0.061788 0.085152 0.118387 0.134416 ... 0.012008
# min 0.003300 0.005500 0.007500 0.011300 ... 0.000000
# 25% 0.080900 0.080425 0.097025 0.111275 ... 0.008425
# 50% 0.106950 0.112100 0.152250 0.182400 ... 0.013900
# 75% 0.154000 0.169600 0.233425 0.268700 ... 0.020825
# max 0.372900 0.459000 0.682800 0.710600 ... 0.100400
#
# V51 V52 V53 V54 V55 V56 \
# count 208.000000 208.000000 208.000000 208.000000 208.000000 208.000000
# mean 0.013420 0.010709 0.010941 0.009290 0.008222 0.007820
# std 0.009634 0.007060 0.007301 0.007088 0.005736 0.005785
# min 0.000800 0.000500 0.001000 0.000600 0.000400 0.000300
# 25% 0.007275 0.005075 0.005375 0.004150 0.004400 0.003700
# 50% 0.011400 0.009550 0.009300 0.007500 0.006850 0.005950
# 75% 0.016725 0.014900 0.014500 0.012100 0.010575 0.010425
# max 0.070900 0.039000 0.035200 0.044700 0.039400 0.035500
#
# V57 V58 V59
# count 208.000000 208.000000 208.000000
# mean 0.007949 0.007941 0.006507
# std 0.006470 0.006181 0.005031
# min 0.000300 0.000100 0.000600
# 25% 0.003600 0.003675 0.003100
# 50% 0.005800 0.006400 0.005300
# 75% 0.010350 0.010325 0.008525
# max 0.044000 0.036400 0.043900
#
# [8 rows x 60 columns]
* (pandas相当于matlab中的元胞数组)
* 读入数据和分析数据
* describe函数自动计算出每一列的均值、方差、分位数
- 相关性分析
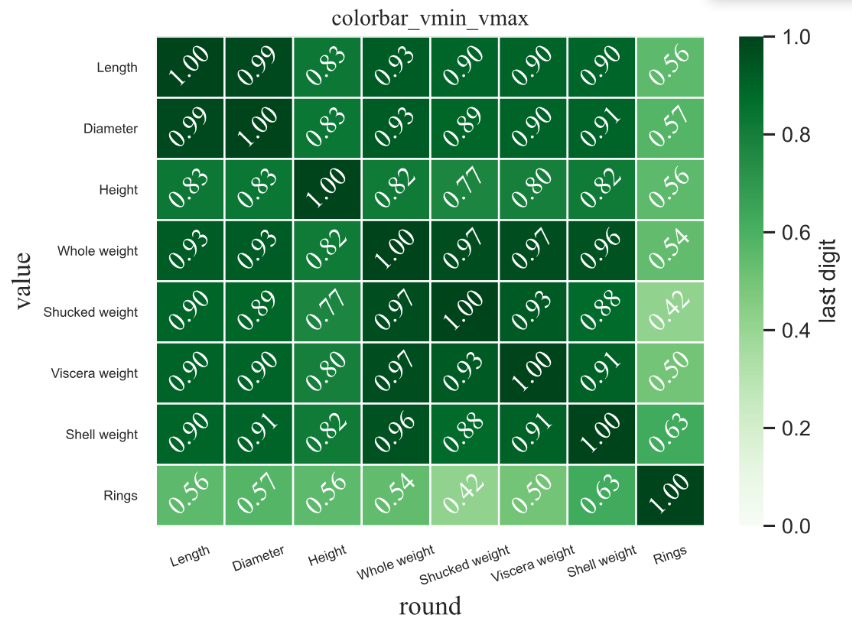
__author__ = 'mike_bowles'
import pandas as pd
from pandas import DataFrame
import matplotlib.pyplot as plot
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import prettytable
#python颜色库
from sklearn import datasets
import seaborn as sns
#参考Python可视化matplotlib&seborn14-热图heatmap - pythonic生物人的文章 - 知乎
#https://zhuanlan.zhihu.com/p/165426873
#matplotlib inline
target_url = ("http://archive.ics.uci.edu/ml/machine-"
"learning-databases/abalone/abalone.data")
#read abalone data
#读取url的文件
abalone = pd.read_csv(target_url,header=None, prefix="V")
#设置列名称
print(abalone.columns)
abalone.columns = ['Sex', 'Length', 'Diameter', 'Height',
'Whole weight', 'Shucked weight',
'Viscera weight', 'Shell weight', 'Rings']
#calculate correlation matrix计算相关矩阵(1到第九列)
df = DataFrame(abalone.iloc[:,1:9].corr())
#print correlation matrix绘制相关矩阵
print(df)
print(df.shape)
df.head()
#设置字体显示中文
plt.rcParams["font.family"] = ["sans-serif"]
plt.rcParams["font.sans-serif"] = ['SimHei']# 用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False # 用来正常显示负号
font1 = {'family' : 'Times New Roman',
'weight' : 'normal',
'size' : 12,
}
#右侧colorbar范围修改
#注意colorbar范围变化,左图颜色随之变化
plt.clf()
fig=plt.figure(dpi=120)
sns.set(font_scale=1.0,style='white',context='notebook')#改变热力图的风格和版式,以及字体缩放大小
ax=sns.heatmap(data=df, #矩阵数据集,数据的index和columns分别为heatmap的y轴方向和x轴方向标签
# cmap选取的颜色条,有的是由浅到深('Greens'),有的是相反的('Greens_r')
cmap=plt.get_cmap('Greens'), # matplotlib中的颜色盘'Greens_r'
vmin=0, #图例(右侧颜色条color bar)中最小显示值
vmax=1, #图例(右侧颜色条color bar)中最大显示值
#center=0, #color bar的中心数据值大小,可以控制整个热图的颜盘深浅
annot=True, #默认为False,当为True时,在每个格子写入data中数据
fmt=".2f", #设置每个格子中数据的格式,参考之前的文章,此处保留两位小数
annot_kws={'size': 14, 'weight': 'normal', 'color': 'white','rotation': 45,'font': font1}, # 设置格子中数据的大小、粗细、颜色
linewidths=1,#每个格子边框宽度,默认为0
linecolor='white',#每个格子边框颜色,默认为白色
#mask=df>0.5,#热图中显示部分数据:显示数值大于0.5的数据
cbar_kws={'label': 'last digit'},
# cbar_kws={'label': 'ColorbarName', #color bar的名称
# 'orientation': 'vertical',#color bar的方向设置,默认为'vertical',可水平显示'horizontal'
# "ticks":np.arange(4.5,8,0.5),#color bar中刻度值范围和间隔
# "format":"%.1f",#格式化输出color bar中刻度值
# "pad":0.15},#color bar与热图之间距离,距离变大热图会被压缩
#xticklabels=['三','关注','py']
xticklabels=True,#x轴方向刻度标签开关、赋值,可选“auto”, bool, list-like(传入列表), or int
yticklabels=True,#y轴方向刻度标签开关、同x轴
)
ax.tick_params(labelsize=7)
# 旋转x轴刻度上文字方向
ax.set_xticklabels(ax.get_xticklabels(), rotation=20)
# 旋转x轴上的刻度
plt.title('colorbar_vmin_vmax',font1)
plt.xlabel('round',font1,fontsize=14)
plt.ylabel('value',font1,fontsize=14)
plt.tight_layout()#保证指标超出边界
#图的输出
#将文件保存至文件中并且画出图,dpi设置高分辨率输出
plt.savefig('figure.svg',dpi=600)
plt.show()