Reliable Conflictive Multi-view Learning论文阅读

irizhang / 2024-10-15 / 原文

发表在AAAI24上的一篇，论文地址：https://ojs.aaai.org/index.php/AAAI/article/view/29546

1. 问题背景

以往的多视图研究，总是假设不同视图的数据是严格对其的，但在实际情况中，无法保证。
实际的多视图数据可能包含低质量的冲突实例，以往采取直接消除或者替换冲突数据，但不应该直接删除，而是在冲突数据中进行决策来判断取哪一方的观点。
一个新的可靠冲突多视图学习（RCML）问题，该问题要求模型为冲突的多视图数据提供决策结果和附加的可靠性。

2. 贡献

认识到在处理相互冲突的多视图数据时显式提供决策结果和相关可靠性的重要性，指出一个新的可靠冲突多视图学习（RCML）问题。
提出了一种针对 RCML 问题的证据冲突多视图学习（ECML）方法。
在多视图融合阶段，提出一种冲突意见聚合策略，并从理论上证明了该策略可以精确地模拟多视图公共和视图特定可靠性的关系。

总体上就是指出了一种RCML问题，并针对该问题提出ECML方法来为冲突的多视图数据提供决策结果和附加可靠性。

3. 模型

问题定义

RCML中，给定一个数据集，每个例子$V$个视图，$\bar{N}$ 个正常实例，$\tilde{N}$ 个冲突实例。就像下面这张图：

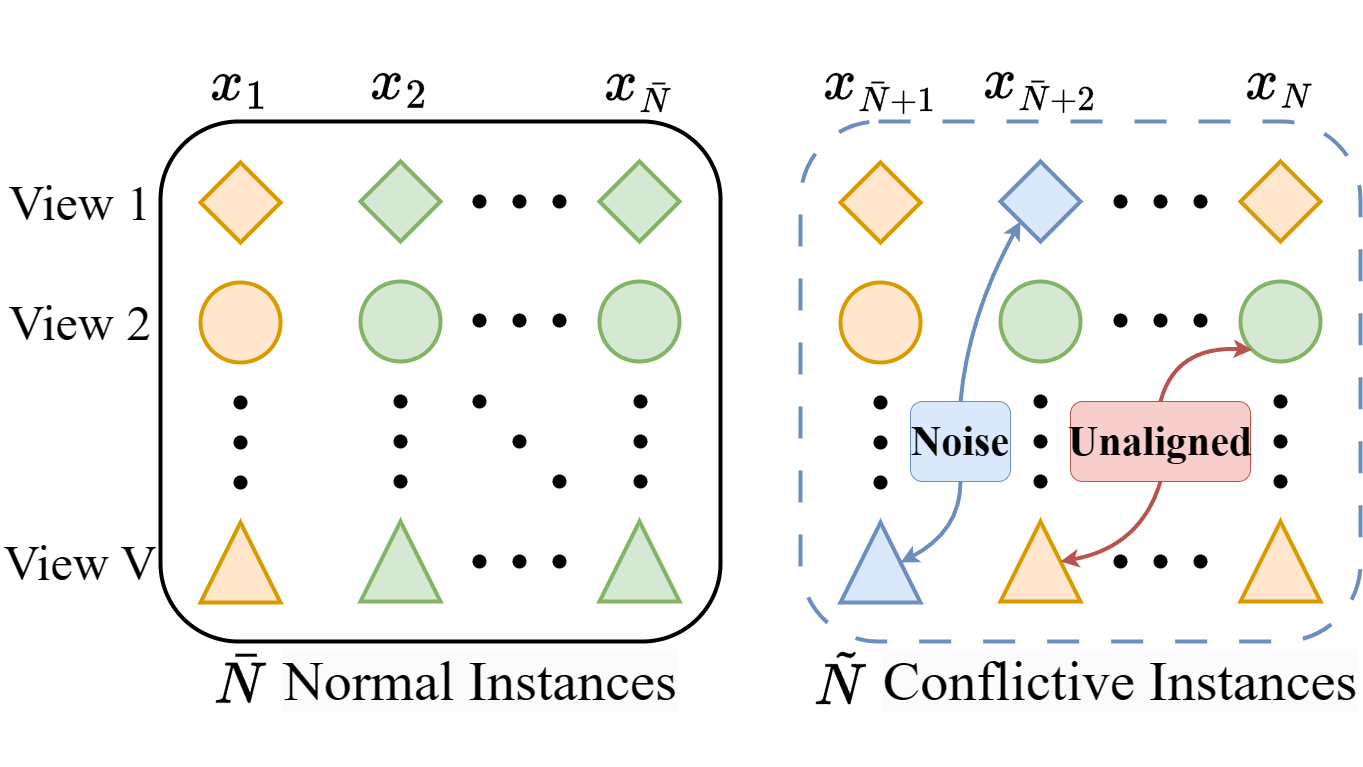
$\mathrm{x}_n^v \in \mathbb{R}^{D_v} (v = 1, \cdots, V)$ 表示第$n$个$(n=1,\cdots,N)$ 实例的第$v$个视图的特征向量，其中$D_v$ 指第$v$个视图的维数。

one-hot向量 $\mathrm{y}_n \in \{0,1\}^K$ 表示第 $n$ 个实例的真实标签，其中 $K$ 是所有类别的总和。

训练元组 $\{ \{\mathrm{x}_n^v \}_{v=1}^V, \mathrm{y}_n \}_{n=1}^{\bar{N}_{train}}$ 包含 $\bar{N}_{train}$ 个正常实例，测试集则由 $\bar{N}$ 剩余部分 $\bar{N} -\bar{N}_{train}$ 和 $\tilde{N}$ 冲突实例组成。

RCML的目的就是准确预测测试集实例的 $\mathrm{y}_n$ （可能相当于决策结果了？），并提供附加的预测不确定性 $u_n \in [0, 1]^1$ 来衡量决策可靠性 $1 - u_n$。

证据冲突多视图学习(EMCL)

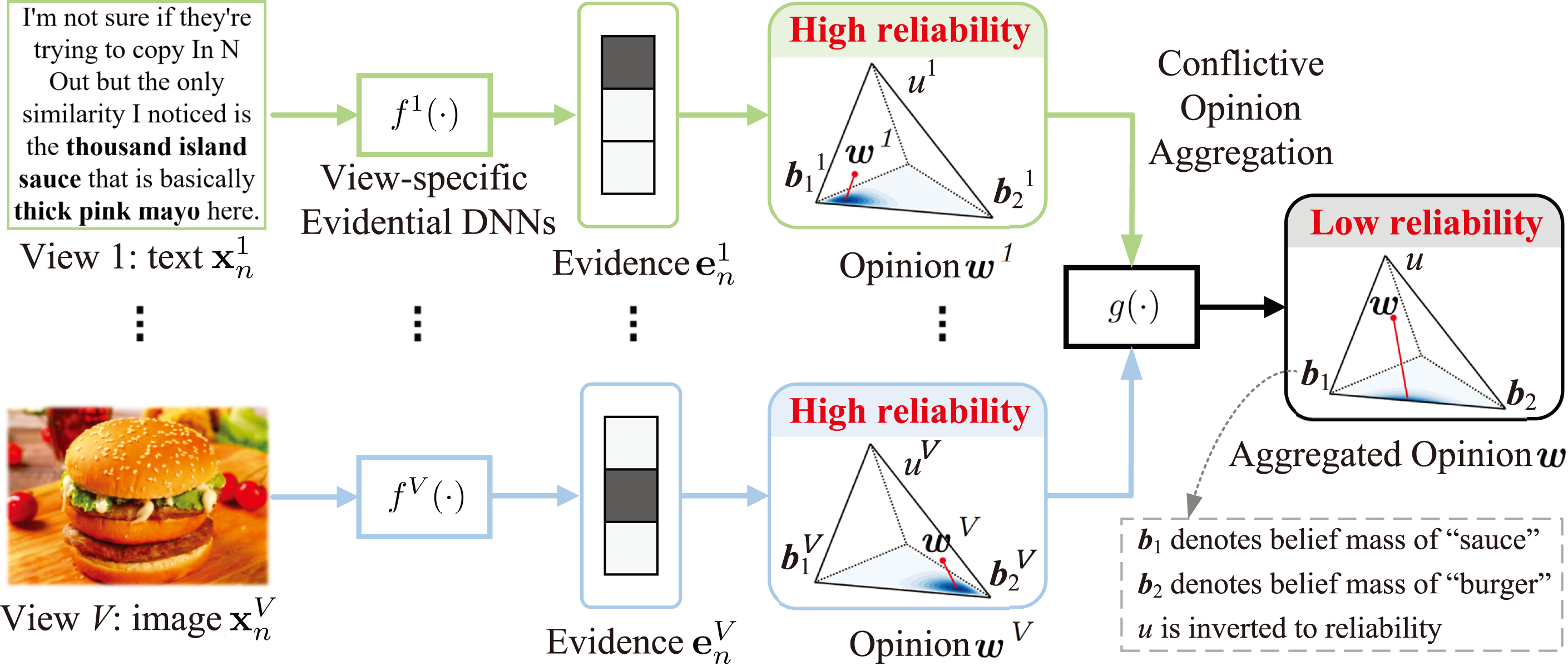
上图所示，整体架构由特定视图的证据学习和证据多视图融合阶段组成。
第一阶段，通过证据 DNN（这里的证据DNN不太了解）从数据中收集的每个类别的支持量。然后，类概率的视图特定分布由狄利克雷分布建模，并使用视图特定证据进行参数化。根据视图之间的预测距离和连接确定性来计算冲突度，通过最小化冲突度，强制特定于视图的 DNN 在训练阶段很好地捕获多视图公共信息。这将减少由特定于视图的 DNN 引起的决策冲突，即由于特定于视图的模型做出错误的决策，正常实例被误认为冲突实例。

特定于视图的证据深度学习

大多数现有的深度多视图学习方法依赖DNN，由于softmax可能导致输出过于自信。为解决这个问题，本文引入了EDL，通过特定视图的证据DNNs $\{ f^v(\cdot)\}_{v=1}^V$来收集证据 $e_n^v$，证据就是指从输入中收集以支持分类过程的量度。（解决上面证据DNN困惑）
（因为上面用到了Dirichlet distribution，个人猜想这相当于找到K-Means聚类中K的值，详情见上面的链接文章，里面介绍到了DP分布解决的就是这一堆点是由多少个高斯分布生成的问题）
对于 $K$ 分类问题，实例 $(\mathrm{x}_n^v)^2$ 的特定视图的多项式意见 $\rightarrow $ 有序三元组 $w = (b, u, a)$ ，其中 置信质量（belief mass）$b = (b_1, \cdots, b_k)^T$ 根据每个值的证据支持将置信质量分配给实例的可能值。不确定性质量 $u$ 捕捉了证据中的模糊性或空虚程度，基准率分布 $a = (a_1, \cdots, a_k)^T $ 表示每个类 k 的先验概率分布。其中$b, u \geq 0$，且任意$b + u = 1$，即：

$\sum_{k=1}^{K}{b_k}+u = 1, \forall k \in [1, \cdots, K].$ 这时，我们就能得出多项式意见的预测概率分布为： $P_k = b_k + {a_k}u, \forall k \in [1, \cdots, K].$ 使用狄利克雷概率密度函数（PDF）用于形成类别分布，可以模拟二阶不确定性。狄利克雷分布的概率密度函数： $D(_P|\alpha) = \left\{\begin{matrix} \frac{1}{B(\alpha)} \prod_{k=1}^K{p_k^{\alpha_k - 1}}, & for\ _P \in S_K,\\ 0, & otherwise, \end{matrix}\right.$ 其中 $p = (p_1, \cdots, p_k)^T $ 是实例被分配到第 $k$ 个类的概率，$\alpha = (\alpha_1, \cdots, \alpha_k)^T $ 表示狄利克雷参数，$S_K$ 是 $K$ 维单位单纯形，定义为： $S_K = \left\{ _P|{\sum_{k=1}^K}p_k = 1\ and \ 0 \leq p_1, \cdots, p_k \leq 1 \right\}$ 狄利克雷模型中的不确定性质量 $u$ 反映了证据的空虚性,将不确定性质量解释为证据的空洞性反映了“观察越少，不确定性质量越多”的特性。用 $ \alpha = e + 1 > 1$ （这里的e是指前面提到收集的证据e）来计算 $\alpha$ 的值，确保狄利克雷分布是非稀疏的。多项式意见和狄利克雷分布之间的映射可以由下式给出： $b_k = \frac{e_k}{S} = \frac{\alpha_k - 1}{S}, u = \frac{K}{S},$ 其中 $S = \sum_{k = 1}^K (e_k + 1) = \sum_{k = 1}^K \alpha_k $, $e = (e_1, \cdots, e_K)^T$。需要注意的是，不确定性水平与可用证据的总量成反比。在没有任何证据的情况下，每种观点的置信度为 0，即达到最大不确定性为1。类概率可以计算为 $p_k = \alpha_k/S $。

通过视图特定的证据学习阶段，最终得到了视图特定的观点和相应的类别分布。

通过冲突意见聚合进行证据多视图融合

根据特定于视图的观点重点介绍多视图融合。多视图我们很难判断哪个视图是高质量的，实际上多视图学习学习更改看重待融合视角的质量。尤其是当两个视图的学习结果发生冲突时。本文提出了一种新的冲突意见聚合方法来解决判断视图质量。

定义 1 冲突意见聚合

$w^A = (b^A, u^A, a^A)$ 和 $w^B = (b^B, u^B, a^B)$ 分别是视图 A 和 B 对同一实例的看法。冲突的汇总意见 $ w^A \underline{\lozenge} w^B = (b^{A \underline{\lozenge} B}, u^{A \underline{\lozenge} B}, a^{A \underline{\lozenge} B}) $ 按以下方式计算：