拓展：三角形四心的向量表示

HT_walnut / 2023-08-01 / 原文

一．“四心”的定义

(1) 重心：三边中线的交点，重心将中线长度分成2：1；

(2) 垂心：三条高线的交点，高线与对应边垂直；

(3) 内心：三条角平分线的交点（内切圆的圆心），角平分线上的任意点到角两边的距离相等；

(4) 外心：三条中垂线的交点（外接圆的圆心），外心到三角形各顶点的距离相等。

二.“四心”的重要结论

重心

$1.$ 已知 $O$ 是 $\Delta ABC$ 所在平面上的一点，若 $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=0$，则 $O$ 是 $\Delta ABC$ 的重心

$2.$ 已知 $O$ 是 $\Delta ABC$ 所在平面上的一点，若 $S_{\Delta OAB} = S_{\Delta OAC} = S_{\Delta OBC} = \frac{1}{3}S_{\Delta ABC}$，则 $O$ 是 $\Delta ABC$ 的重心

$3.$ 已知 $O$ 是 $\Delta ABC$ 所在平面上的一点，若动点 $P$ 满足
$\overrightarrow{OP}=\overrightarrow{OA}+\lambda (\overrightarrow{AB}+\overrightarrow{AC}),\lambda \in (0,+\infty )$，则 $P$ 的轨迹一定通过 $\Delta ABC$ 的重心

$4.$ 已知 $O$ 是 $\Delta ABC$ 所在平面上的一点，若动点 $P$ 满足
$\overrightarrow{OP}=\overrightarrow{OA}+\lambda (\overrightarrow{AB}+\frac{1}{2}\overrightarrow{BC}),\lambda \in (0,+\infty )$，则 $P$ 的轨迹一定通过 $\Delta ABC$ 的重心

$5.$ 已知 $O$ 是 $\Delta ABC$ 所在平面上的一点，若动点 $P$ 满足
$\overrightarrow{OP}=\overrightarrow{OA}+\lambda (\frac{\overrightarrow{AB}}{|AB|sinB}+\frac{\overrightarrow{AC}}{|AC|sinC}),\lambda \in (0,+\infty )$，则 $P$ 的轨迹一定通过 $\Delta ABC$ 的重心

垂心

$1.$ 已知 $O$ 是 $\Delta ABC$ 所在平面上的一点，若 $\overrightarrow{OA}\cdot \overrightarrow{OB} =\overrightarrow{OB}\cdot \overrightarrow{OC} = \overrightarrow{OA}\cdot \overrightarrow{OC}$，则 $O$ 是 $\Delta ABC$ 的垂心

$2.$ 已知 $O$ 是 $\Delta ABC$ 所在平面上的一点，若 $\left | \overrightarrow{OA} \right | ^ 2 + \left | \overrightarrow{BC} \right | ^ 2 = \left | \overrightarrow{OB} \right | ^ 2 + \left | \overrightarrow{AC} \right | ^ 2 = \left | \overrightarrow{OC} \right | ^ 2 + \left | \overrightarrow{AB} \right | ^ 2$，则 $O$ 是 $\Delta ABC$ 的垂心

$3.$ 已知 $O$ 是 $\Delta ABC$ 所在平面上的一点，若动点 $P$ 满足
$\overrightarrow{OP}=\overrightarrow{OA}+\lambda (\frac{\overrightarrow{AB}}{|AB|cosB}+\frac{\overrightarrow{AC}}{|AC|cosC}),\lambda \in (0,+\infty )$，则 $P$ 的轨迹一定通过 $\Delta ABC$ 的垂心

内心

$1.$ 已知 $O$ 是 $\Delta ABC$ 所在平面上的一点，若动点 $P$ 满足
$\overrightarrow{OP}=\overrightarrow{OA}+\lambda (\frac{\overrightarrow{AB}}{|AB|}+\frac{\overrightarrow{AC}}{|AC|}),\lambda \in (0,+\infty )$，则 $P$ 的轨迹一定通过 $\Delta ABC$ 的内心

$2.$ 已知 $O$ 是 $\Delta ABC$ 所在平面上的一点，若动点 $P$ 满足
$\overrightarrow{OP}=\overrightarrow{OA}+\lambda (\frac{\overrightarrow{AB}}{sinC}+\frac{\overrightarrow{AC}}{sinB}),\lambda \in (0,+\infty )$，则 $P$ 的轨迹一定通过 $\Delta ABC$ 的内心

$3.$ 已知 $O$ 是 $\Delta ABC$ 所在平面上的一点，$a,b,c$ 为 $\Delta ABC$ 的三边的边长，若 $a\cdot \overrightarrow{OA} + b\cdot \overrightarrow{OB} + c\cdot \overrightarrow{OC} = 0$，则 $O$ 是 $\Delta ABC$ 的内心

外心

$1.$ 已知 $O$ 是 $\Delta ABC$ 所在平面上的一点，若 $\left | \overrightarrow{OA} \right | = \left | \overrightarrow{OB} \right | = \left | \overrightarrow{OC} \right |$，则 $O$ 是 $\Delta ABC$ 的外心

$2.$ 已知 $O$ 是 $\Delta ABC$ 所在平面上的一点，若 $(\overrightarrow{OA} + \overrightarrow{OB})\cdot \overrightarrow{AB} = (\overrightarrow{OB} + \overrightarrow{OC})\cdot \overrightarrow{BC} = (\overrightarrow{OA} + \overrightarrow{OC})\cdot \overrightarrow{CA}$，则 $O$ 是 $\Delta ABC$ 的外心

$3.$ 已知 $O$ 是 $\Delta ABC$ 所在平面上的一点，若动点 $P$ 满足
$\overrightarrow{OP}=\frac{\overrightarrow{OB} + \overrightarrow{OC}}{2}+\lambda (\frac{\overrightarrow{AB}}{|AB|cosB}+\frac{\overrightarrow{AC}}{|AC|cosC}),\lambda \in (0,+\infty )$，则 $P$ 的轨迹一定通过 $\Delta ABC$ 的外心

$4.$ 已知 $O$ 是 $\Delta ABC$ 的外心，点 $D，E，F$ 分别为边 $AB,AC,BC$ 的中点

$\overrightarrow{AO}\cdot \overrightarrow{AB} =\frac{1}{2}\left | \overrightarrow{AB} \right |^2，\overrightarrow{AO}\cdot \overrightarrow{AC} =\frac{1}{2}\left | \overrightarrow{AC} \right |^2$

$\overrightarrow{BO}\cdot \overrightarrow{BC} =\frac{1}{2}\left | \overrightarrow{BC} \right |^2，\overrightarrow{BO}\cdot \overrightarrow{BA} =\frac{1}{2}\left | \overrightarrow{BA} \right |^2$

$\overrightarrow{CO}\cdot \overrightarrow{CA} =\frac{1}{2}\left | \overrightarrow{CA} \right |^2，\overrightarrow{CO}\cdot \overrightarrow{CB} =\frac{1}{2}\left | \overrightarrow{CB} \right |^2$

拓展

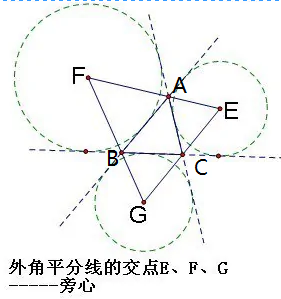
$1.$ 旁心

与三角形的一边及其他两边的延长线都相切的圆叫做三角形的旁切圆，旁切圆的圆心叫做三角形旁心。三角形的一条内角平分线与其他两个角的外角平分线交于一点，即三角形的旁心。

$2.$ 奔驰定理

已知 $O$ 是 $\Delta ABC$ 内一点，$S_{\Delta OBC} \cdot \overrightarrow{OA} + S_{\Delta OAC} \cdot \overrightarrow{OB} + S_{\Delta OAB} \cdot \overrightarrow{OC} = 0$

推论

$1.$ 若 $O$ 为 $\Delta ABC$ 的重心 $\Leftrightarrow $ $S_{\Delta OBC} : S_{\Delta OAC} : S_{\Delta OAB} = 1:1:1$ $\Leftrightarrow $ $\overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} = 0$

$2.$ 若 $O$ 为 $\Delta ABC$ 的内心 $\Leftrightarrow $ $S_{\Delta OBC} : S_{\Delta OAC} : S_{\Delta OAB} = a:b:c$ $\Leftrightarrow $ $a\cdot \overrightarrow{OA} + b\cdot \overrightarrow{OB} + c\cdot \overrightarrow{OC} = 0$

$3.$ 若 $O$ 为 $\Delta ABC$ 的外心 $\Leftrightarrow $ $S_{\Delta OBC} : S_{\Delta OAC} : S_{\Delta OAB} = sin2A:sin2B:sin2C$ $\Leftrightarrow $ $sin2A\cdot \overrightarrow{OA} + sin2B\cdot \overrightarrow{OB} + sin2C\cdot \overrightarrow{OC} = 0$

$4.$ 若 $O$ 为 $\Delta ABC$ 的垂心 $\Leftrightarrow $ $S_{\Delta OBC} : S_{\Delta OAC} : S_{\Delta OAB} = tanA:tanB:tanC$ $\Leftrightarrow $ $tanA\cdot \overrightarrow{OA} + tanB\cdot \overrightarrow{OB} + tanC\cdot \overrightarrow{OC} = 0$

$3.$ 三角形各心之间的关系

$(1)$ 外心与重心

设 $\Delta ABC$ 的外心为 $O$，则 $G$ 为 $\Delta ABC$ 的重心的充要条件是 $\overrightarrow{OG} = \frac{1}{3}(\overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC})$