每日一💧_堆
每日一💧_堆
时隔五百多年,我又开始写博客了。为啥隔了这么久呢?因为哥们我acm打完退役力。拿银之后一直在摆烂偷懒 哈哈
现在有了新的目标,开始考研所以要开始规律愉快的学习。写写博客咯~~希望我可以做到日更!!!!!
对了,为啥叫每日一💧呢?因为我偶像写的叫【每日一🔥】
回归正题,啥是堆?其实就是priority_queue,但是之前都是直接调stl,没有了解过底层原理。所以今天来仔细研究一下。
1堆的定义
堆一般来说有大根堆和小根堆。普通的堆就是一棵二叉树,树上每个节点的权重都大于等于或者小于等于其子节点。
2堆的实现
如下图,就是一个很标准的小根堆。
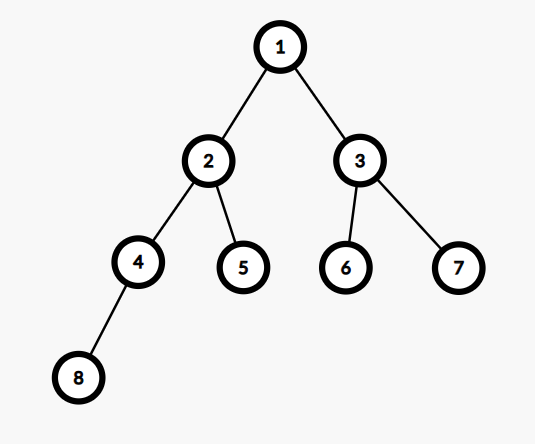
很神奇的是,这棵树的节点编号就是其在数组中存储的下标。所以加点的时候只要直接丢到一维数组的最后面(堆底),然后维护有序即可。
删点操作的时候,一般的优先队列只会去弹堆顶,但是我们手写堆就高端了,可以去删除任意节点(方法是一样的)。只要将要删除节点和堆底节点交换然后维护有序即可。
维护有序。加点和删点两个操作都涉及到维护有序,那么这是如何实现的呢?其实很简单。只要像冒泡排序那样一路冒泡就行了。
在给出代码之前,为了增强可读性,我画了个小图。个人习惯将当前节点叫做now,他的儿子叫做nxt,他的爸爸叫做pre。
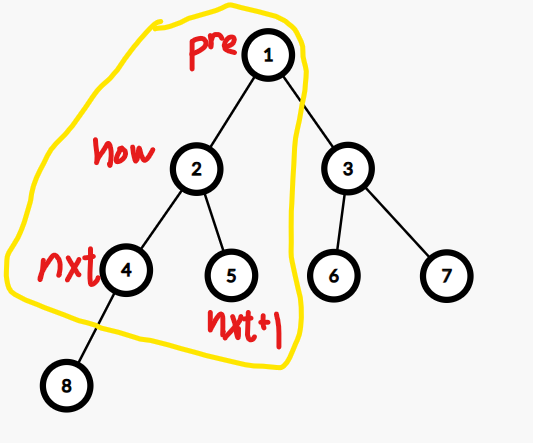
堆模板题链接
下面给出维护小根堆的代码:
ll tr[N] , cnt ;
void push(ll x){
tr[ ++ cnt] = x ;
ll now = cnt ;
while(now > 1){
ll pre = now >> 1 ;
if(tr[now] < tr[pre]){
swap(tr[now] , tr[pre]) ;
now = pre ;
}else break ;
}
}
void pop(){
swap(tr[1] , tr[cnt]) ;
cnt -- ;
ll now = 1 ;
while((now<<1) <= cnt){//存在左儿子
ll nxt = now << 1 ;
if(nxt+1 <= cnt && tr[nxt+1] < tr[nxt]) ++nxt ;
if(tr[now] > tr[nxt]) swap(tr[now] , tr[nxt]) ;
else break ;
now = nxt ;
}
}
void solve(){
ll q ;
cin >> q ;
while(q -- ){
ll op , x ; cin >> op ;
if(op == 1){
cin >> x ;
push(x) ;
}else if(op == 2){
cout << tr[1] << "\n" ;
}else pop() ;
}
}//code_by_tyrii
提一嘴,看完这个实现方法我们可以发现,堆的插入删除时间复杂度是很铁的logn。
3优先队列重载运算符
实际使用的时候,一般都用priority_queue而且一般往堆里面塞的时候都是塞的结构体。这个时候就需要对其进行优先级的自定义,也就是常说的重载运算符。
struct Node{
ll a , b ;
bool operator<(const Node&x) const {
if(x.a == a) return x.b < b ;
return x.a < a ;
}
};
4对顶堆
这个其实貌似没什么用
P1801 黑匣子
题意:在插入过程中去查询第k大
思路:做一个对顶堆(一个大根一个小根)。要找第k大就是找大根堆大小为k时的堆顶。还是比较妙的。画个图理解一下:
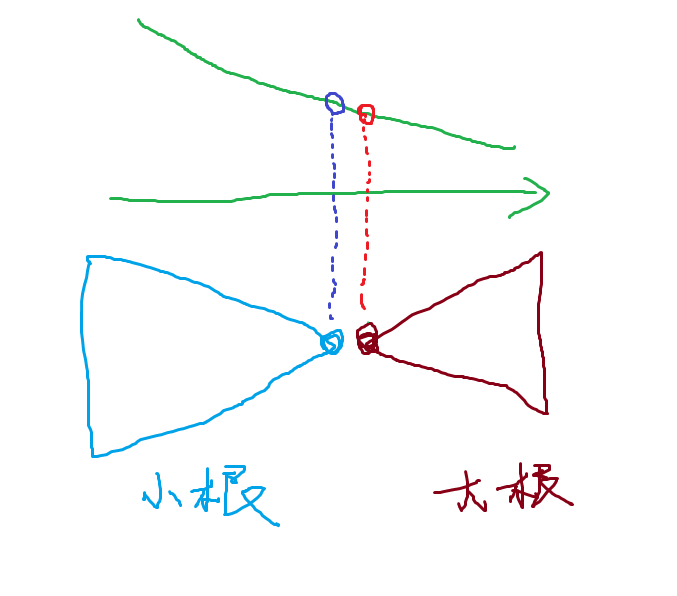
void solve(){
cin >> n >> m ;
rep(i , 1 , n) cin >> a[i] ;
rep(i , 1 , m) cin >> st[i] ;
priority_queue<ll , vct<ll> , greater<ll> > q2 ;
priority_queue<ll> q1 ;
rep(i , 1 , m){
int tot = q1.size()+q2.size() ;
rep(j , tot+1 , st[i]){
q1.push(a[j]) ;
}
while(q1.size() > i-1){
q2.push(q1.top()) ;
q1.pop() ;
}
cout << q2.top() << "\n" ;
q1.push(q2.top()) ;
q2.pop() ;
}
}