NOI2023补题
D1T1
前置知识:扫描线
首先问题是所有线的并集大小,我们可以想到相交的两条线是可以合并的,在合并之后,第一种线和第二种线可以直接用扫描线求并集。
而第三种线最多只有 \(5\) 条,我们先将第三种线的大小全部加到答案上,然后直接枚举第一种和第二种线与这 \(5\) 条线求交点,直接减去就行,注意可能三种线交于一点,直接用 \(map\) 维护这个电是否被统计过就行,\(ez\)。
D2T2
很好的题(指打了 \(4\) 个板子)。
前置知识:主席树(也许不用)、后缀数组、manacher 算法、树状数组
先进行一个很典的操作,先在原串后面加一个隔离点,再将原串翻转然后接到后面,即得到了新的串 \(s\)
(\(s_{ n+1-i } = s_{n+1+i}\) \(i \in \left[ 1,n\right]\)),位置$n+1+i \in \left [ 1,n \right] $ 的后缀即是原串翻转后的\(s\left [1:n+1-i\right ]\)。
然后算出后缀数组,那么我们知道了每个后缀的排名。 排名越大那么此后缀的字典序越大。
我们再考虑我们要统计的答案,对于一个询问 \(i,r\),我们要求有多少个 \(l\) 满足 \(s\left [ i:i+l-1 \right ]\) 的字典序小于翻转后的 \(s\left [ i+l:i+2\times l-1 \right ]\) 的字典序,我们想到如果 \(s\left [ i:i+l-1 \right ]\) 与翻转后 \(s\left [ i+l:i+2 \times l-1 \right ]\) 字典序不相同,那么我们只需要比较 \(s\left [i :n\right ]\)与翻转后的 \(s\left [1:i+2 \times l-1 \right ]\) 字典序大小即可。
这个在得到后缀排序的排名后,就是一个查询在 \(\left [ i+1,i+2 \times l-1\right ]\) 对应的翻转位置上有多少个数大于当前数了,用主席树或其他数据结构就能解决,注意由于我们要求的点其实是 \(i+2 \times l-1\) 而由于 \(2 \times l\),所以查的点是\(i+2-1,i+4-1,i+6-1\),要进行奇偶分别建树。
然后我们只需要将 \(s\left[ i,i+2\times l-1\right]\) 是回文串的情况进行去重就行了。我们可以发现回文串都是偶回文串,用 \(manacher\) 可以很轻松得找出所有偶回文串,我们考虑每个回文串对每个询问的贡献,假设每个回文串为 \(\left [ L,R\right ]\),偏左的回文中心为 \(mid\),那么只有 \(L \le i\),且 \(mid \le i+r-1\) 的询问才会被这个影响到。
如果我们直接进行差分统计,将 \(c\left[ L-1\right]--\),\(c\left[ mid\right]++\),那么统计 \(\left[ i,i+r-1\right]\) 时会把下面这种情况包含
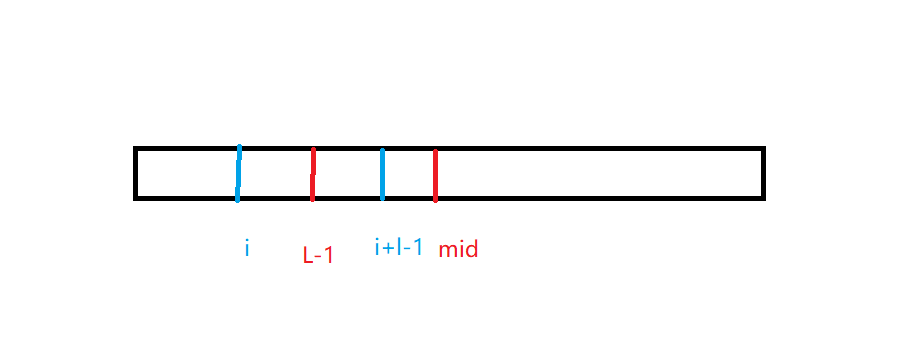
我们可以发现这种情况是 \(mid > i+r-1\) 的,那么我们将询问按 \(i+r-1\)排序,再依次在查答案的时候将 \(mid \le i+r-1\) 的插到差分数组里,我们就能直接查 \(\left[ i,i+r-1\right]\) 进行去重。
注意,还有一种情况是是回文串,但是后缀排序要小于前面的串,在一开始统计没统计上,但是后面去重却删掉了,那么我们可以想到,这种情况是在这个最大回文串的左边一个字符小于右边一个字符的时候出现,在去重加入差分的时候特判不要加入贡即可。