躲避拥挤

flatte / 2023-07-29 / 原文

小明很想出去走走。但是小明讨厌太拥挤的地方，她会拒绝一些人气旺盛的道路。有n个景点，有m双向道路。每条道路有一个人气值d ，表示这条道路的拥挤程度。小明不会经过那些人气值大于x的道路，他想知道有多少对景点 (a,b)使得从a景点出发可以到达b景点。

第一行一个整数 T，表示有T 组数据。

对于每组数据，第一行有三个数n,m,q ，q 表示有 q 组询问。

接下来 m 行，每行三个数x,y,d ，表示有一条连接 x,y，人气值为 d 的道路。

最后 q 行，每行一个整数 x，代表询问。

对于每组数据，输出q行，依次回答所有询问。

样例输入

样例输出

2
6
12

样例解释：

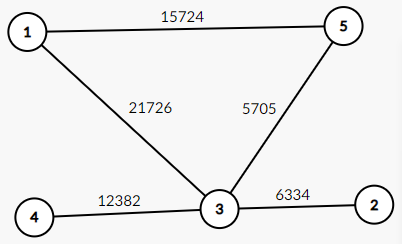
拥挤程度不超6000的道路有2--->3，有2对景点符合条件。分别是（2，3）（3，2）

拥挤程度不超10000的道路有2--->3，3--->5，有6对景点符合条件。（2，3）（3，2）（3，5）（5，3）（2，5）（5，2）

拥挤程度不超13000的道路有2--->3，3--->5，3--->4有12对景点符合条件。（2，3）（3，2）（3，5）（5，3）（2，5）（5，2）（4，3）（3，4）（2，4）（4，2）（4，5）（5，4）

分析：

求边长不大于x的各个连通块中元素个数c，景点对数为A(c,2)。累加所有连通块中的景点对数。

连接两个联通块A，B ，其中景点分别个数为cnt_A和cnt_B

则贡献的景点对数为 cnt_A*cnt_B*2

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 #define re register 
 4 #define LL long long
 5 
 6 const int MAXN = 2e4+10;
 7 int T,fa[MAXN];
 8 int cnt[MAXN];//cnt[i] 记录i所在的联通分量中的景点个数 
 9 LL ans[MAXN];//ans[i] 记录第i个询问的答案。 
10  
11 inline int find(int x){
12     if(fa[x]==x) return x;
13     cnt[fa[x]]+=cnt[x];cnt[x]=0;
14     return fa[x]=find(fa[x]);  
15 }
16 
17 inline void write(long long x)//长整型数据输出 
18 {
19      if(x < 0){putchar('-'); x = -x;}
20     if(x > 9)write(x / 10); putchar((x % 10) ^ 48);
21     return;
22 }
23  
24 struct nod1{int x,y,d;}edges[MAXN*5]; 
25 inline int cmp1(nod1 a,nod1 b) {return a.d<b.d;} //按拥挤程度从小到大排序 
26  
27 struct nod2{int id,x;}query[MAXN*5]; 
28 inline int cmp2(nod2 a,nod2 b) {return a.x<b.x;} //按忍受极限从小到大排序
29  
30 int main() {
31      
32     cin>>T;
33     while(T--){
34          
35         int n,m,q;cin>>n>>m>>q;
36         for (re int i=1;i<=n;i++) cnt[i]=1,fa[i]=i;
37          
38         for (re int i=1;i<=m;i++) cin>>edges[i].x>>edges[i].y>>edges[i].d;           
39         sort(edges+1,edges+1+m,cmp1);//按拥挤程度从小到大排序
40      
41         for (re int i=1;i<=q;i++) cin>>query[i].x,query[i].id=i;         
42         sort(query+1,query+1+q,cmp2); //按忍受极限从小到大排序        
43         
44         LL res=0;
45         int edinx=1;//边序号,边已经按照拥挤程度从小到大排序了             
46         for(re int i=1;i<=q;i++) //按忍受极限从小到大处理每个询问 
47         {                        
48             //遍历每一条拥挤程度不大于忍受极限的边。            
49             while((edinx<=m)&& (edges[edinx].d<=query[i].x))    
50             { 
51                 int l=find(edges[edinx].x);
52                 int r=find(edges[edinx].y);
53                 if(l!=r)//x,y不属于同一个联通分量，那要合并成一个联通分量。 
54                 {
55                     fa[l]=r;//合并
56                     
57                     //合并两个联通分量，增加了景点对数
58                     res+=(LL)cnt[l]*cnt[r]*2;
59                     //后一个询问的忍受极限一定大于等于前一个询问，
60                     //所以后一个询问的结果继续累加，不能清零。 
61                     
62                     //合并后的大联通分量中的景点个数，为之前两个小联通分量之和。 
63                     cnt[r]+=cnt[l]; 
64                     cnt[l]=0;                     
65                 }
66                 edinx++;  //处理下一条边 
67             } 
68             ans[query[i].id]=res; //按原来的询问顺序记录答案            
69         }
70         
71         // 按原来的询问次序输出答案
72         for(re int i=1;i<=q;i++) {
73             write(ans[i]);
74             //puts("");
75         }          
77     }
78     return 0;
79 }