SCU预备役Day 1
2023-07-28 22:13:56
基本算法
二分与三分
使用范围:答案具有单调性时。
原理:判断远比求解简单
定义域:
- 为整数域的时候,若区间长度为N,则需要进行log2N次运算
- 为实域的时候,判断R-L精度是否达到要求,需要R-L>=eps(但因为实数运算带来的精度问题,若eps太小会导致是循环,往往指定二分次数更好)
整数域:
1 while(l<r){ 2 int mid=(l+r)>>1; 3 if(check(mid)) r=mid; 4 else l=mid+1; 5 return l; 6 } 7 8 while(l<r){ 9 int mid=(l+r+1)>>1; 10 if(check(mid)) l=mid; 11 else r=mid-1; 12 return l; 13 } 14 15 while(l<=r){ 16 int mid=(l+r)>>1; 17 if(check(mid)) ans=mid,l=mid+1; 18 else r=mid-1; 19 }
实数域:
while(fabs(l-r)>dlt){ mid=(l+r)/2.0; if(check(mid)) r=mid; else l=mid; }
还有一种方法:如果指定二分次数为t,那么结束时区间长度为L/pow(2,t),根据这个值是否符合我们的精度就可以了。
三分模板
使用范围:求凸性函数的极值问题(单峰函数)

#include<bits/stdc++.h> using namespace std; int n; double l,r,a,b,c,d; double s[20]; double ans(double x){ double sum=0,t=1.0; for(int i=1;i<=n;i++){ t*=x; sum+=s[i]*t; } return sum; } bool check(double m1,double m2){ if(ans(m1)>ans(m2)) return true; else return false; } int main(){ cin>>n>>l>>r; for(int i=1;i<=n;i++){ cin>>s[n-i+1]; } int k; cin>>k; while(fabs(l-r)>=0.00001){ double m1=l+(r-l)/3.0,m2=r-(r-l)/3.0; if(check(m1,m2)) r=m2; else l=m1; } cout<<(l+r)/2.0<<endl; return 0; }
前缀和与差分:
典例1:求L - R 区间的和
Sum[r]-Sum[l]
二维情况:
复杂度:O(nm)
Sum[a][b]=sum[a-1][b]+sum[a][b-1]-sum[a-1][b-1]+x[a][b];
如果求(x1,y1)到(x2,y2)的矩阵和的话就是s[x2,y2]-s[x1-1,y2]-s[x2,y1-1]+s[x1-1,y1-1];
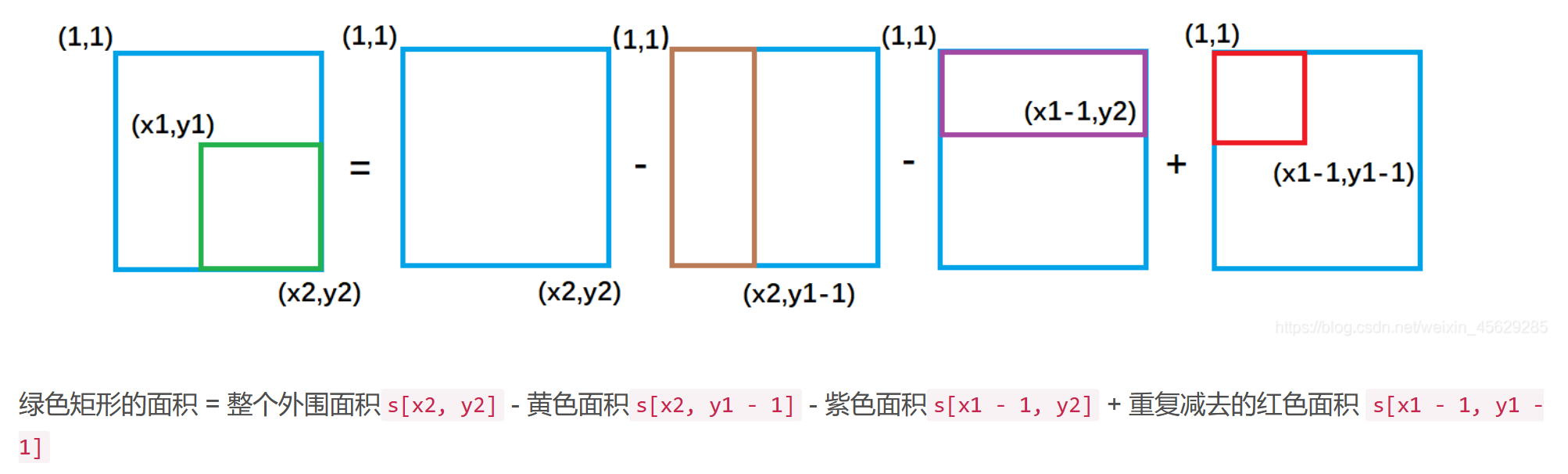
类似于数学中的求导和积分,差分可以看成前缀和的逆运算。
差分数组:
首先给定一个原数组a:a[1], a[2], a[3],,,,,, a[n];
然后我们构造一个数组b : b[1], b[2], b[3],,,,,, b[i];
使得 a[i] = b[1] + b[2] + b[3] + ,,,,,, + b[i]
也就是说,a数组是b数组的前缀和数组,反过来我们把b数组叫做a数组的差分数组。 换句话说,每一个a[i]都是b数组中从头开始的一段区间和。
何构造差分b数组:
a[0 ]= 0;
b[1] = a[1] - a[0];
b[2] = a[2] - a[1];
........
b[n] = a[n] - a[n - 1];
运用:m个操作,将区间[l,r]的数都加上c,最后输出区间数组。
我们知道a数组是b的前缀和,那么b[l]+c会影响l之后的a数组,最后我们再打个补丁:b[r+1]-c。
二维差分
构造公式:b[i][j]=a[i][j]-a[i-1][j]-a[i][j]+a[i-1][j-1];

void insert(int x1,int y1,int x2,int y2,int c) { //对b数组执行插入操作,等价于对a数组中的(x1,y1)到(x2,y2)之间的元素都加上了c b[x1][y1] += c; b[x2 + 1][y1] -= c; b[x1][y2 + 1] -= c; b[x2 + 1][y2 + 1] += c; }
位运算
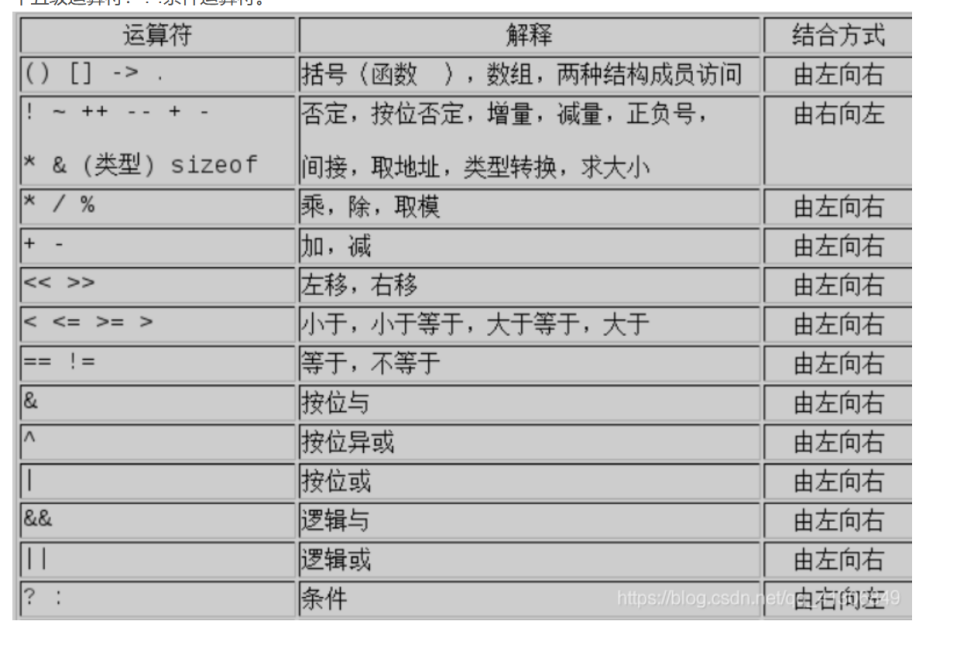
运算符优先情况
常见技巧

^(异或运算的运算法则)
1. a ^ b = b ^ a
2. a ^ b ^ c = a ^ (b ^ c) = (a ^ b) ^ c;
3. d = a ^ b ^ c 可以推出 a = d ^ b ^ c.
4. a ^ b ^ a = b.
问题定义:有2n+1个数,只有一个单着,别的都是成对的,找出这个单着的数。比如:2 1 3 2 1。
答:异或计算,一趟搞定。时间复杂度o(n),答案为3,因为两个相同的数异或为0.
问题:1-1000放在含有1001个元素的数组中,只有唯一的一个元素值重复,其它均只出现一次。每个数组元素只能访问一次,设计一个算法,将它找出来;不用辅助存储空间,能否设计一个算法实现?
解答:
令,1^2^…^1000(序列中不包含n)的结果为T
则1^2^…^1000(序列中包含n)的结果就是T^n。
T^(T^n)=n。
所以,将所有的数全部异或,得到的结果与1^2^3^…^1000的结果进行异或,得到的结果就是重复数。
问题: 在一堆数中,有且仅有两种数,出现了奇数次,而其他种的数,都出现了偶数次,请找出出现了奇数次的这两种数。
int main() { int a=0,b=0;//设出现奇数次的数为a,b int t=0,i; int rightone;//二进制下,从右往左的第一个1 int arr[20]; for( i=0;i<20;i++) { t^=arr[i]; } //现在的t==a^b,这两个出现奇数次的数异或 //因为t==a^b; //a!=b //所以t的二进制肯定有一位上是1 rightone=t&(~t+1); //一个数与(&)上自己取反+1的数,结果得到这个数二进制下最右侧的1 //并且我们知道,a和b两者在这一位上,只有一者位上是1,另一个一定是0. for(i=0;i<20;i++) { if(t^arr[i]==0)//将该最右位是1和0的区分开 { a^=arr[i];//此时a等于一种奇数次数^一些出现过偶数次数且该位也是1的数 //而出现偶数次可以抵消,所以直接得到了第一个出现了奇数次的数 } } b=t^a;//由此再得到b }
Bitset的使用
Bitset<N>
今日好题
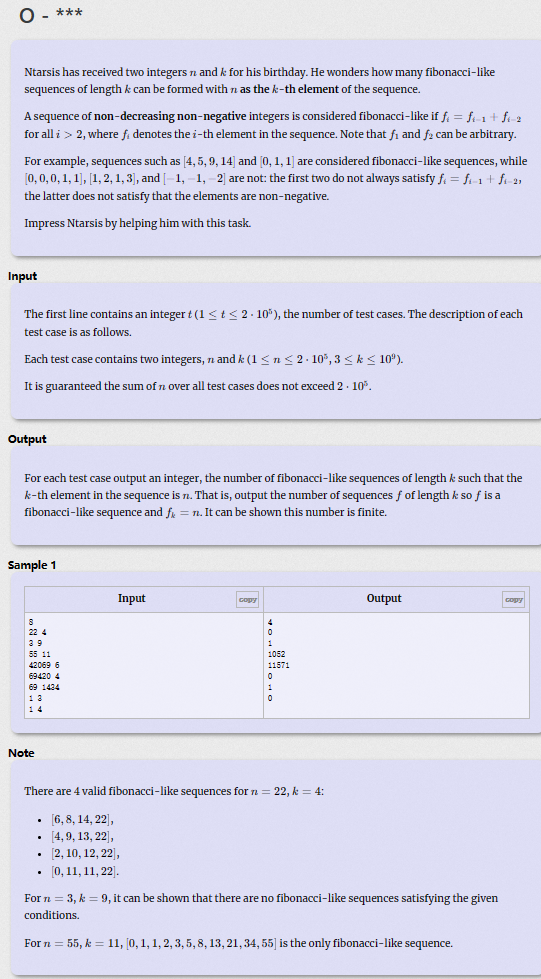
发现这个数列只与前两个数有关,假设弄成二维,前四项为(1,0),(0,1),(1,1),(1,2)可以发现对于单独的x方向和y方向又分别构成了斐波拉契数列且xi=fib(i-2),yi=fib(i-1)。
另一个重点是 fib(30)约等于8e5,远远超过了本体范围,那么我们只需要预处理30位的fib即可。
最终问题转化成ax+by=n的二元一次方程问题(易错的是y>=n)
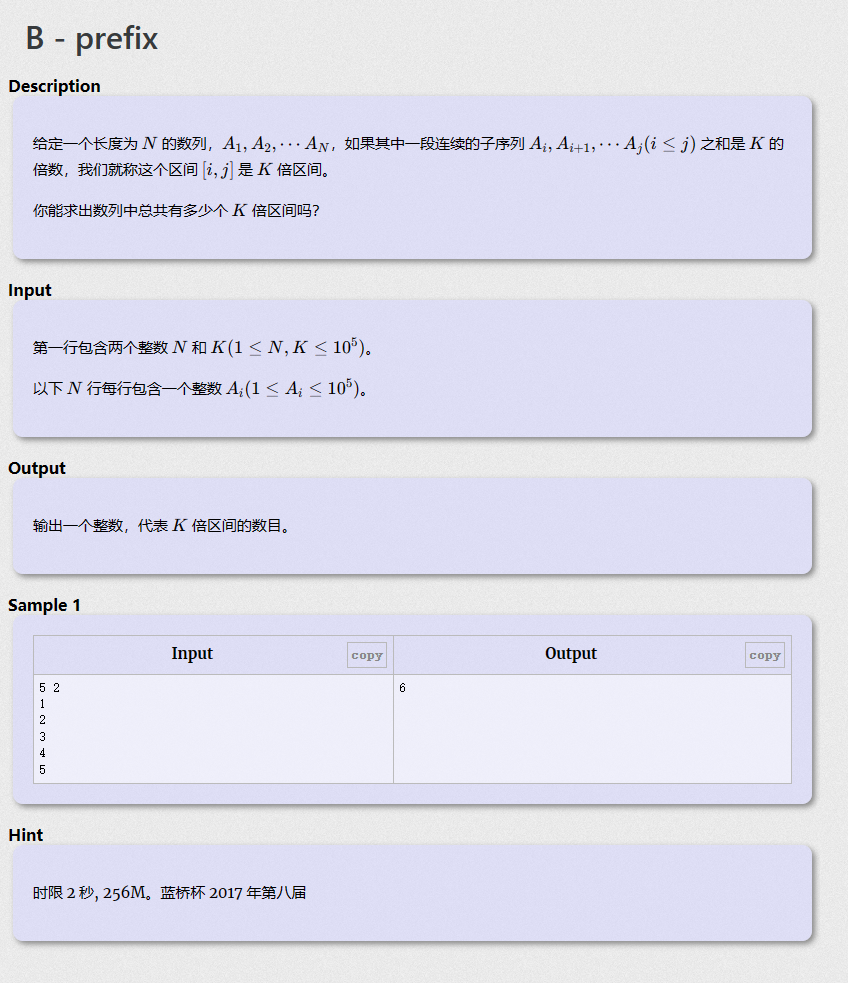
思路:
首先可以肯定的是需要用到前缀和的思想,但是最后发现遍历s数组的时候复杂度n2会TLE。
解决关键:同余定理
当是s[i]和s[j]%k之后若余数相同则s[i+1]到s[j]为所求
最后我们用桶排序处理答案

正宗的斐波拉契数列