SIFT
一些基础:
图像的一阶导数和二阶导数
一阶

参考文章:
(103条消息) 【opencv】18.数字图像一阶导数、二阶导数的数学原理_二阶导数图像_Mister Zhu的博客-CSDN博客
二阶

直接用二阶模板和图像进行卷积
边缘检测:
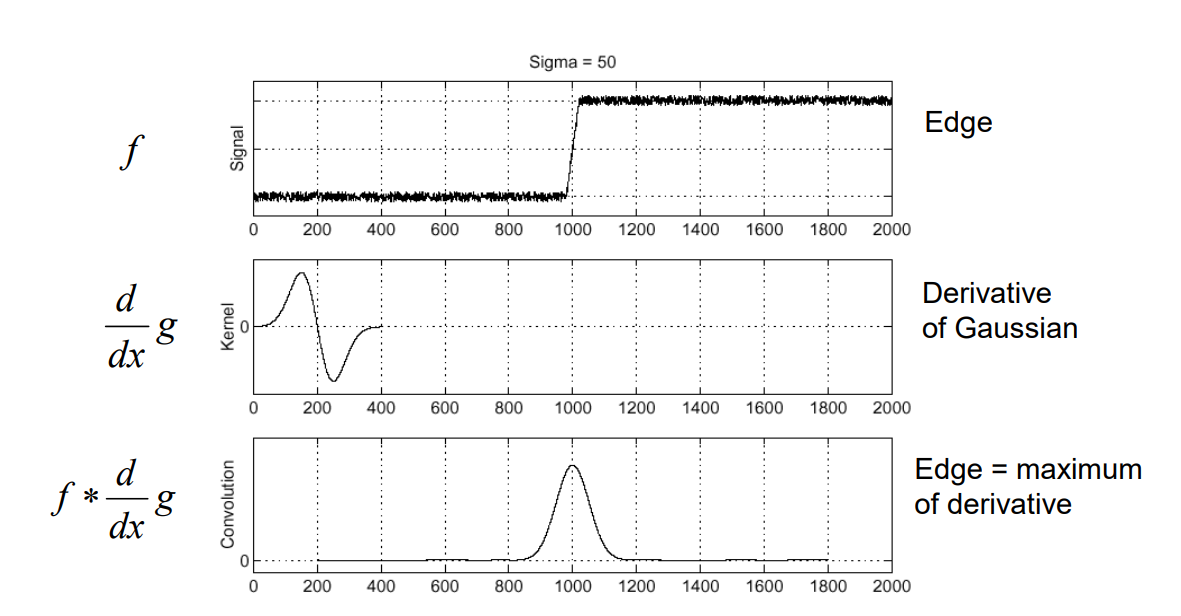
高斯一阶导求边缘
1.一个图像卷积高斯一阶导这意味着做了两件事情:
-
- 对图像进行高斯模糊
- 对高斯模糊的图像求一阶导
2.这些一阶导数取极值的地方就是边缘
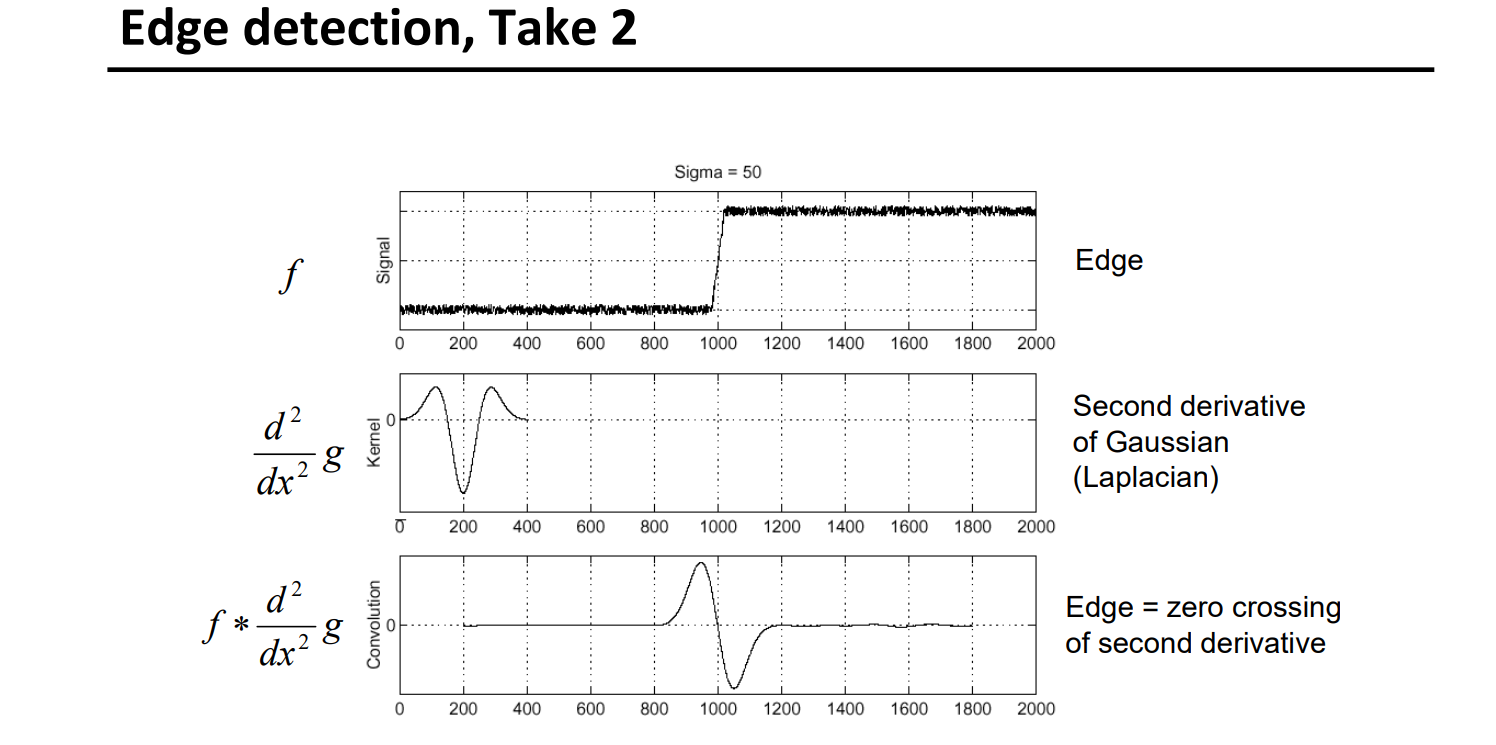
同理,高斯二阶导(也称为拉普拉斯核)为0的地方就是边缘(二阶导数为0,一阶导数取极值)
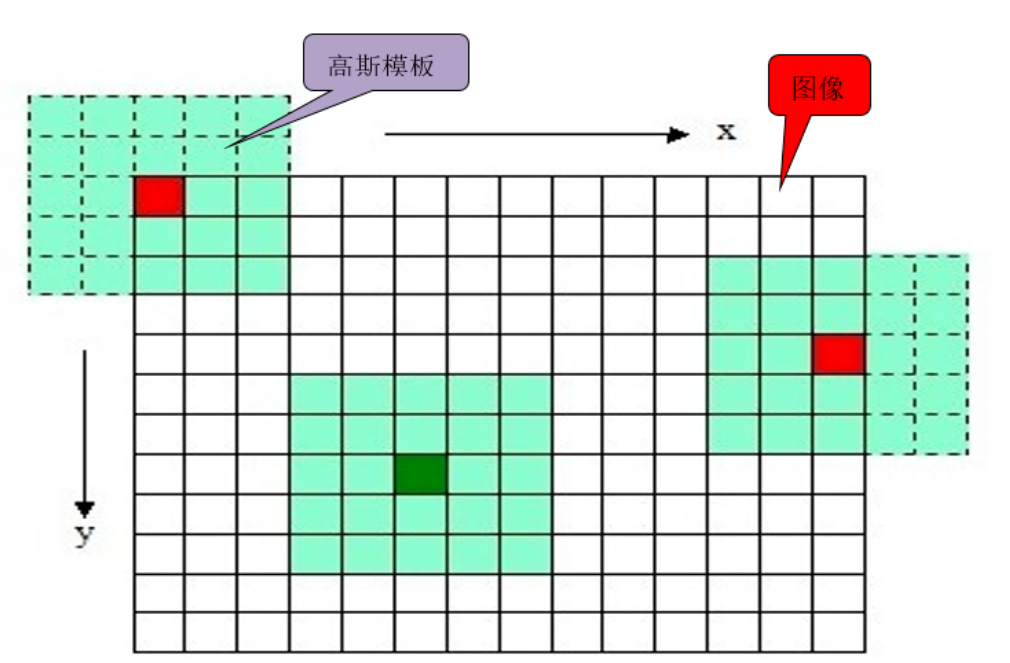
高斯核的方差σ和高斯核的窗口大小的关系:
根据3σ原则,高斯核的窗口大小N=大于6σ+1的第一个奇数。
高斯核的方差和信号响应的关系

上图表明信号和高斯核匹配的时候就能产生极值(原理有空了解下)
我们实际运用的时候是信号尺度未知,我们采用不同方差的高斯核核信号匹配,但是这会带来一些问题
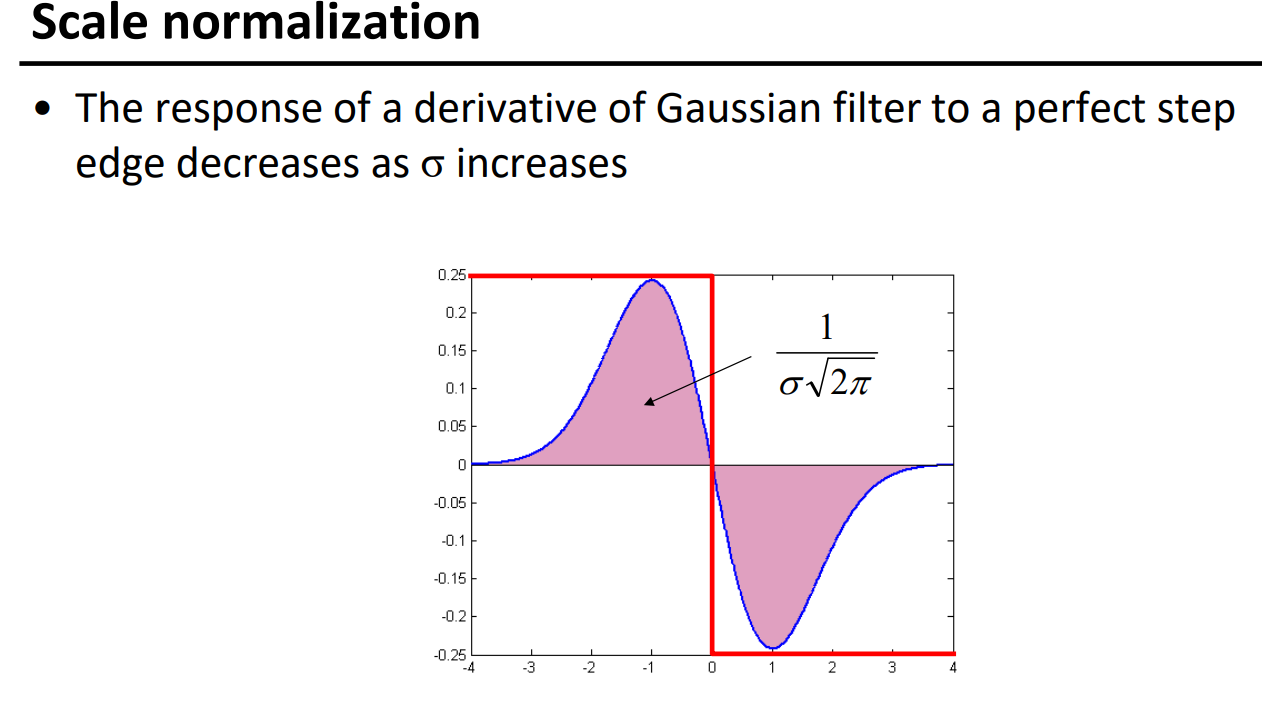
如果我信号的幅值当成1的话,信号和高斯卷积后的面积,就会随着方差的增大而越来越小,导致我们找不到极值
因此我们要做尺度归一化,也就将所有的响应值乘以方差σ,这是一阶的情况,二阶就要乘以σ2(1/σ√2Π,怎么来的了解下)
最后只需记住当卷积核的尺寸(由σ决定)和信号匹配的时候,信号能得到一个响应极值。
面积最大化的情况(之后再去理解)
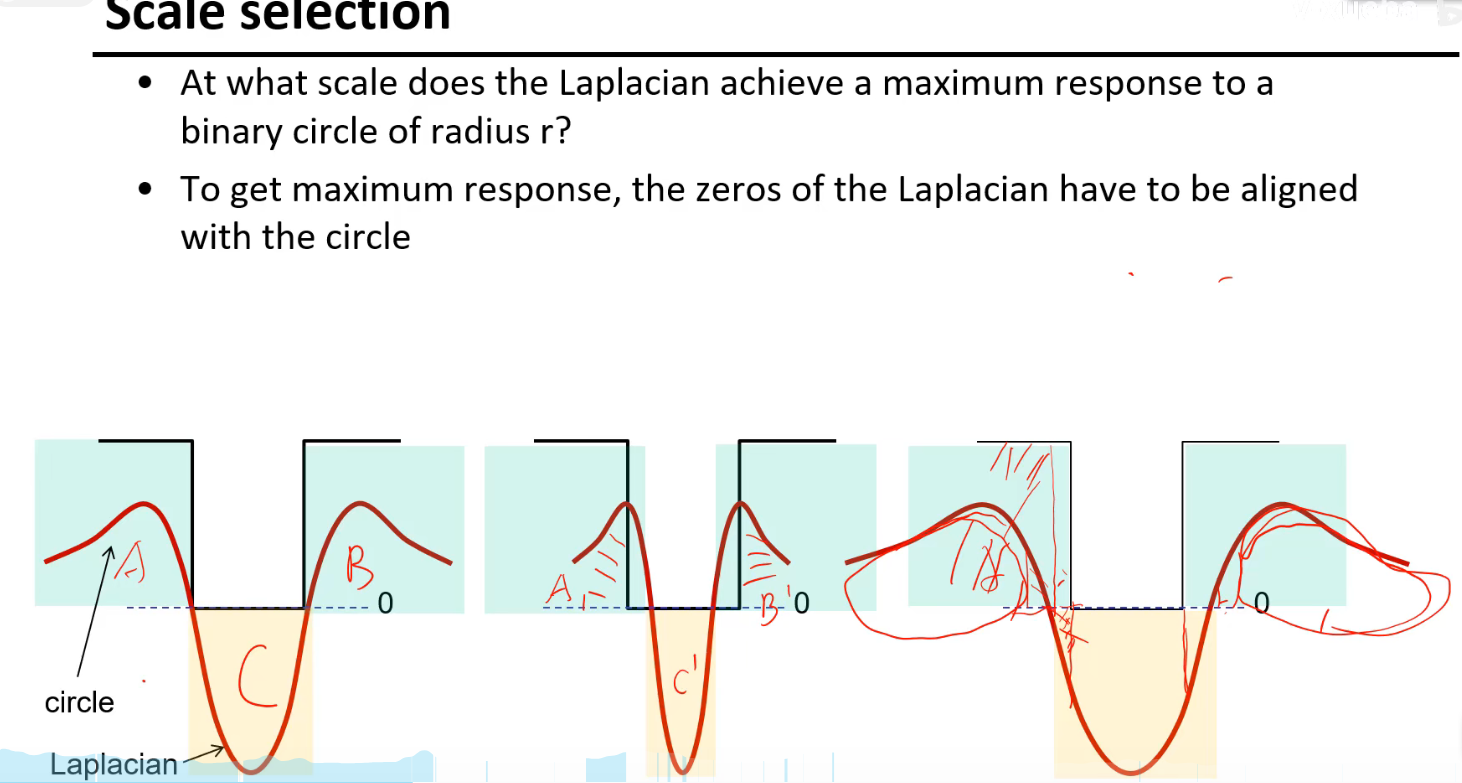
只有第一种情况:信号正好嵌入这个沟中,红线和黑线(信号)相乘的结果和x轴围成的面积才是最大的
嵌进去的一半的长度就是下图中的圆的半径
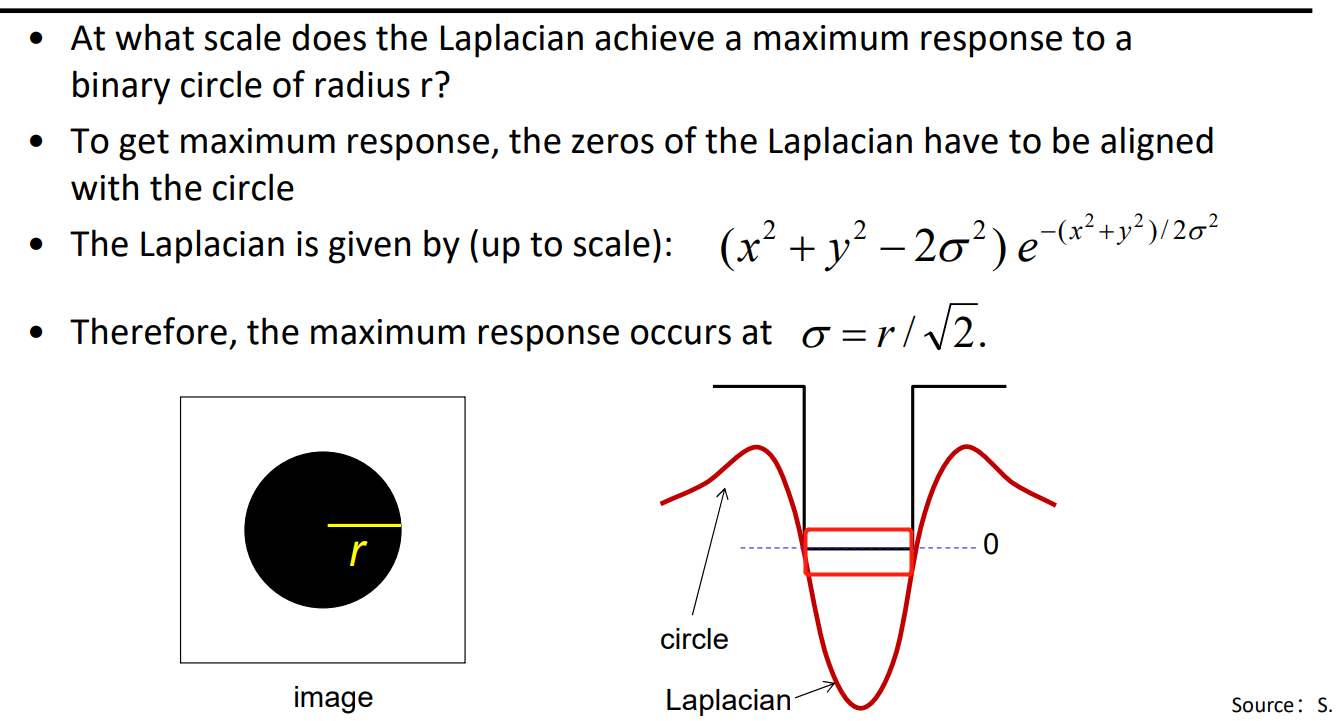
这个圆方程就是使这个二维拉普拉斯算子为0求得的,即x2+y2=2σ2半径就是√2σ,也就是那个红框内一半的长度,也就是信号
SIFT算法:
根据上述可知匹配圆的半径为√2σ
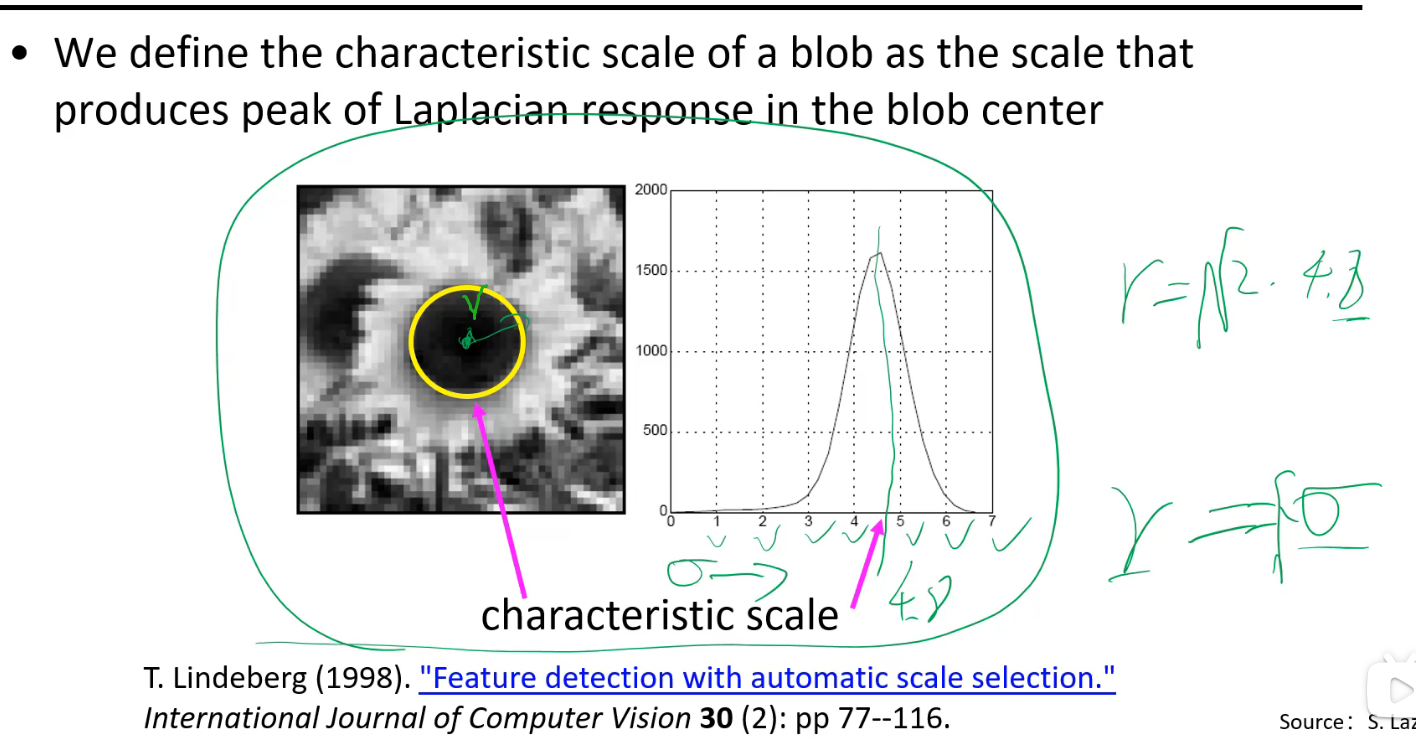
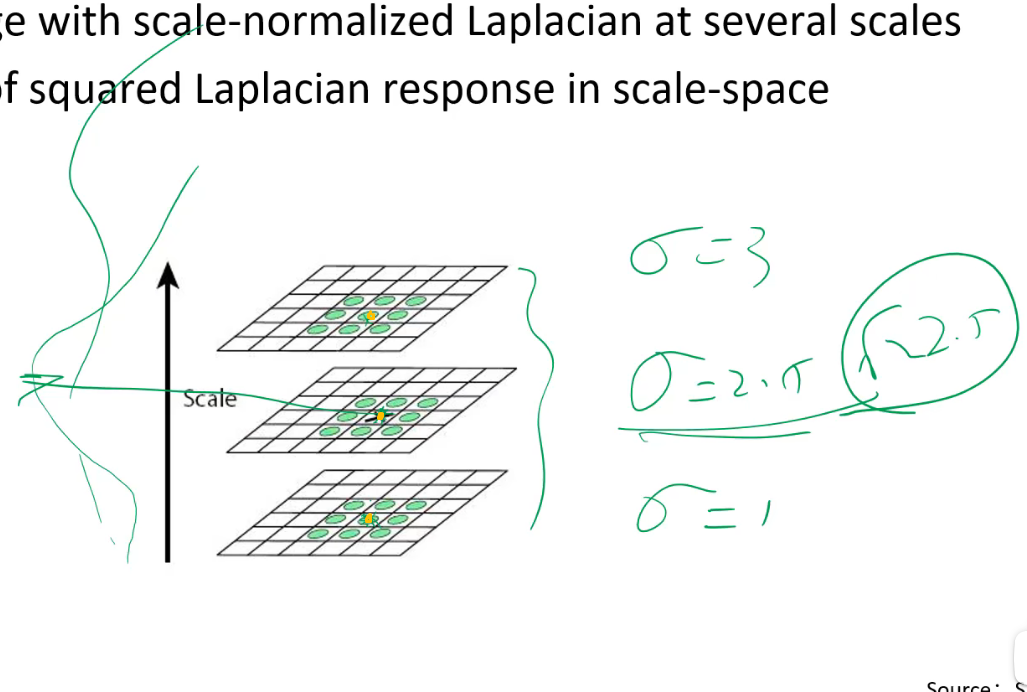
三个黄色的点中哪个响应函数值最大,就用哪一点所在那一层的σ就求匹配圆的半径。
问题是
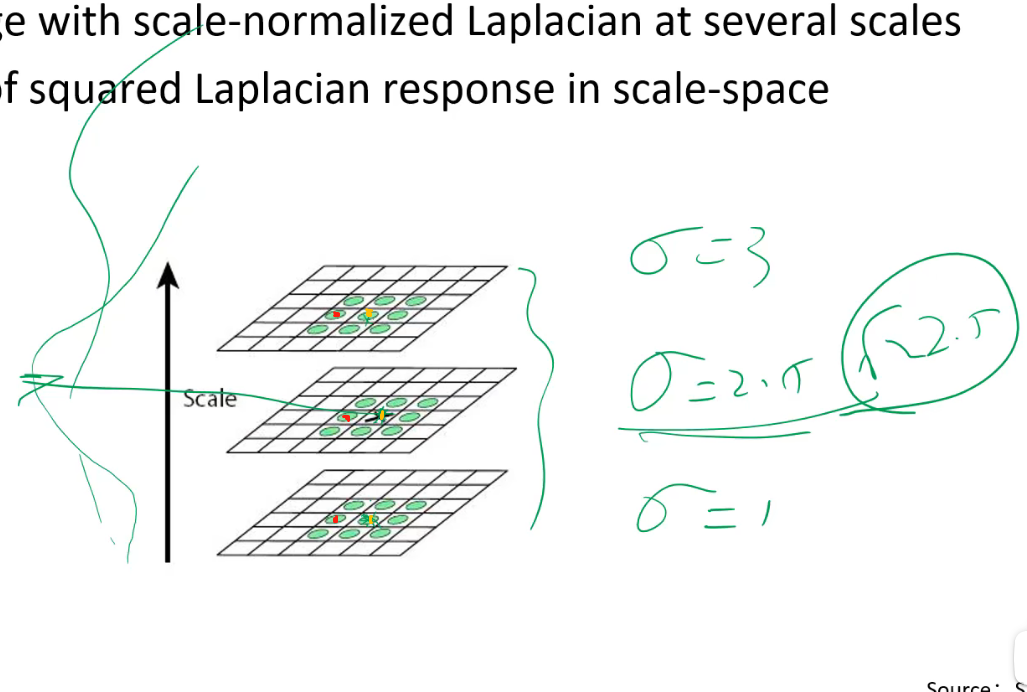
当我中间层的红色的点是三个红点最大的我确定一个匹配圆,当中间的黄色点是三个黄色点中最大的我确定一个匹配圆,而相差一个像素的两个像素几乎是描述同一个东西,因此这就导致了同一个东西对应了同样大小的两个圆,这显然是没必要的,因此采用极大抑制。
如果某一点在这三层邻域内的27个点(这里的27表示我们有三层,如果有4层的话就是36了)中所对应的响应函数值最大,那么就取那个点所在层的σ去计算匹配圆的半径,但是这个点不能来自边界层,也就是只能在中间那层选
拉普拉斯算核(也就是高斯的二阶导)计算量太大,随着σ的增大,模板的窗口大小也增大,大到我几乎要算一个像素点的响应值的时候我几乎要将整个图像的像素点都要和拉普拉斯模板卷积一下。
我们采用高斯差分核
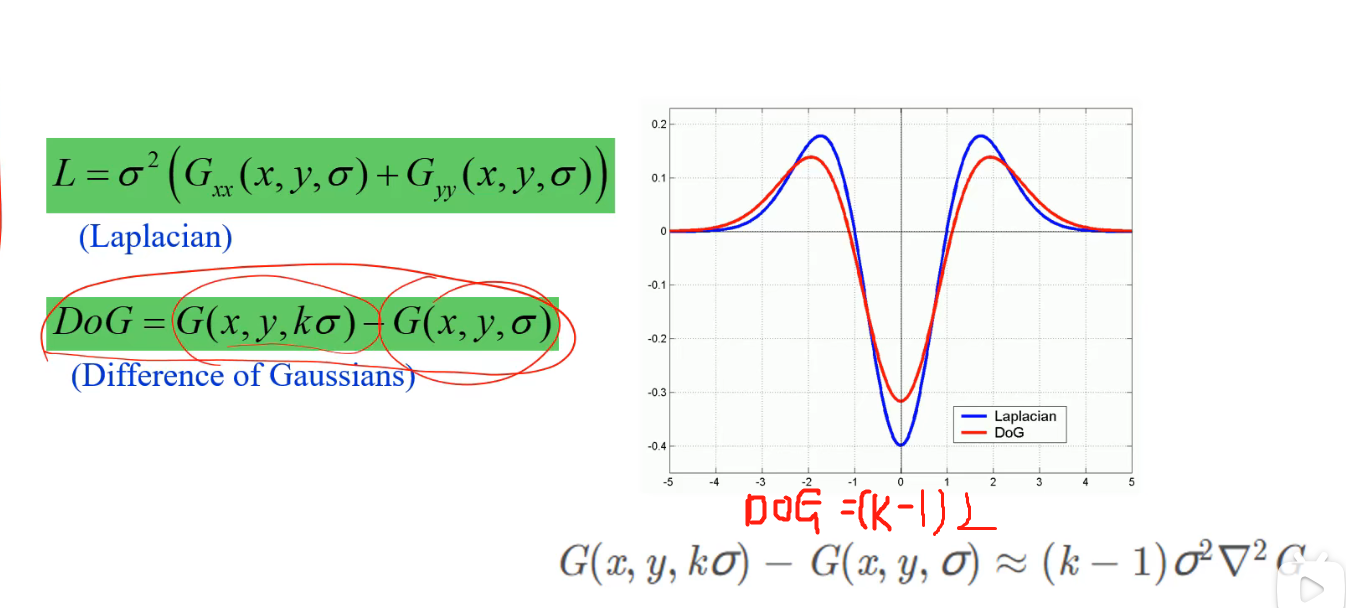
实现步骤:
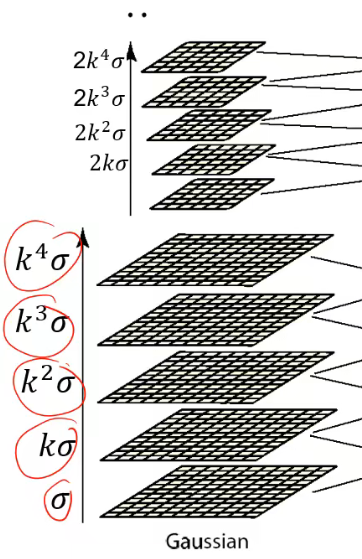
高斯差分金字塔的建立:
高斯金字塔的建立:
1.层数和组数的确定:

——————————————————————————————————————————————————
备注:
n的含义:
假设高斯金字塔每组有S = 5层,则高斯差分金字塔就有S-1 = 4层,那我们只能在高斯差分金字塔每组的中间2层图像求极值(边界是没有极值的),所以n = 2
——————————————————————————————————————————————————
2.每组的图像大小的确定