考研高数笔记
基于《张宇30讲》
1. 高数预备知识
1.1 函数概念
反函数
\(f[f^{-1}(x)]=x\)
严格单调函数必有反函数,有反函数的不一定是单调函数
形如 \(f[f(x)]\) 的复合函数分析方法:1.广义化带入;2. 画图分段分析
有界性
必须指明区间
单调性
注意定义法的判别形式:
\(f(x)\)是单调增函数:\((x_1-x_2)[f(x_1)-f(x_2)]>0\)
\(f(x)\)是单调减函数:\((x_1-x_2)[f(x_1)-f(x_2)]<0\)
\(f(x)\)是单调不减函数:\((x_1-x_2)[f(x_1)-f(x_2)]\geq0\)
\(f(x)\)是单调不增函数:\((x_1-x_2)[f(x_1)-f(x_2)]\leq0\)
奇偶性
偶函数\(y=f(x)\)关于\(y\) 轴对称,且当 \(f'(0)\) 存在时,必有 \(f'(0)=0\)
\(y=f(x)\) 关于直线 \(x=T\) 对称的充分条件是 \(f(x)=f(2T-x)\) 或 \(f(x+T)=f(T-x)\)
四性综合
奇函数求导变偶函数,偶函数求导变奇函数。
连续奇函数的一切原函数都是偶函数,连续偶函数的原函数中仅有 \(\int_0^x f(t)dt\)一个奇函数
连续函数 \(f(x)\) 以 \(T\) 为周期且 \(\int_0^T f(x)dx=0\),则 \(f(x)\) 的一切原函数也以 \(T\) 为周期
若 \(f(x)\) 在 \((a,b)\) 内可导且 \(f'(x)\) 有界,则 \(f(x)\) 在 \((a,b)\) 内有界
1.2 函数图像
根据幂函数单调性简化函数分析方法
原理:\(x>0\) 时,\(y=x\) 与 \(y=\sqrt x, y=\sqrt[3] x,y=lnx\) 有相同单调性,与 \(y=\frac1x\) 有相反单调性。
因此:
对于 \(\sqrt u\) 和 \(\sqrt[3]u\),可直接用 \(u\) 来研究最值(直接去根号求导)
对于 \(|u|\),可直接用 \(u^2\) 来研究最值
对于 \(u_1u_2u_3\),用 \(lnu_1+lnu_2+lnu_3\) 来研究最值
对于 \(\frac1u\),用 \(u\) 来研究最值(注意结论相反)!!
一些常见面积

一个常见极限:
三角函数结论
\(arcsinx+arccosx=\frac{\pi}{2}(-1\leq x\leq 1)\)
\(arctanx+arccotx=\frac{\pi}{2}(-\infty\leq x\leq +\infty)\)
以上结论可通过证常函数的方法来证:即证\(f'=0且f(x_0)=c\)
初等函数
定义域可以是孤立的点
符号函数 \(sgnx\)
取整函数 \(x-1<[x]\leq x\)
在\(x=0\) 的小邻域内,\(|sinx|=sin|x|\)
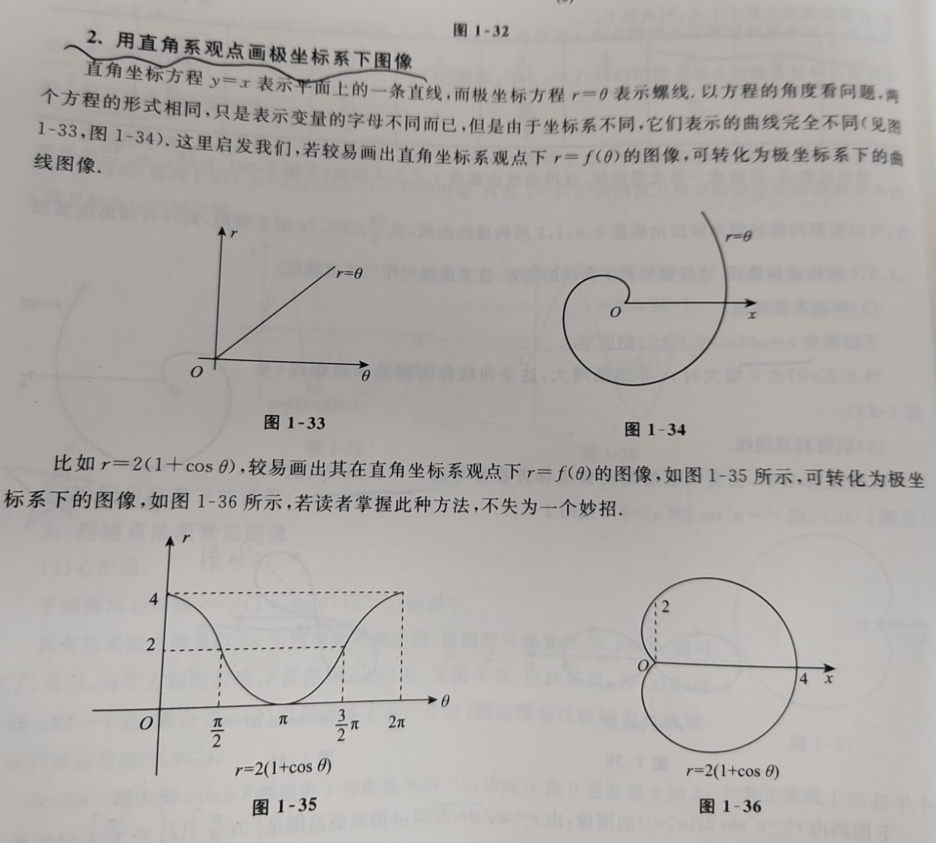
极坐标图像
非常重要的方法:用直角系观点画极坐标系下的图像