构造选做

不倒霉de熊哥 / 2023-07-25 / 原文

全都是玄学

$\mathcal{Part}\ 1$ 抽屉原理

构造题中遇到 $\le\left \lceil \dfrac{n}{k} \right \rceil $ 这样的对于操作次数的限制，可以将所有的操作分成 $k$ 组，每一组都保证能满足题目的要求，这样至少有一组是符合条件的。

常用分组方法：染色法，按剩余系分组，直接构造 $k$ 种方案。

CF1534D Lost Tree

点此看题

不会做绿题了 qwq

问一次距离可以让我们得到以钦定询问点为根时所有点的深度，以及所有与询问点相邻的边（回答的距离为 $1$ 时可以直接连边）。

题目中要求询问次数 $\le\left \lceil \dfrac{n}{2} \right \rceil $，提示我们要把所有点分成两组，而且每一组的点的邻居要覆盖整棵树，可以发现树是二分图，可以黑白染色，等价于按照第一次询问的深度 $\bmod\ 2$ 的剩余系分类，取较小的一组询问可以通过。

CF1450C2 Errich-Tac-Toe

点此看题

猜测和 $\bmod\ 3$ 的剩余系有关。

看一下简单版，如果行列上每三个点就有一个 O，一定符合条件，那么可以按照行数 + 列数 $\bmod\ 3$ 的剩余系分类，枚举把哪一组变成 O，一定有一组满足条件。

回到原题，如果行列上每三个点就有两种颜色，一定符合条件，按照剩余系分类，钦定两个剩余系分别填上 X$/$O 是符合限制的，并且一个点最多会被两个方案包含，分别被填上 X$/$O，等价于一共有 $2k$ 个元素，根据抽屉原理操作最少的一种不会超过 $\left \lceil \dfrac{k}{3} \right \rceil $。

Mine Sweeper II

点此看题

看起来不能染色，和剩余系更是没啥关系，直接构造 $2$ 种不交的方案。

首先有一种很 sb 的构造：直接把原图改成目标图。

~~按照套路改成它的反图（把地雷改成空地，空地改成地雷）也是符合条件的，手玩验证一下发现事实就是这样。~~

考虑数字之和的实际意义，每一对相邻的地雷和空地对会对数字之和产生 $1$ 的贡献，所以我们构造出来的方案要满足相邻的地雷和空地对数量和目标图相等，可以直接沿用原来的相邻对，把地雷改成空地，空地改成地雷不会破坏原来的相邻对，同样符合条件，显然这和上面那个 sb 构造是不交的，满足次数限制。

构造中有要求某种元素数量相等时，可以考虑在不改变原有元素的基础上做变换。

$\mathcal{Part}\ 2$ dfs 树

在无向图上连通性相关和环相关的问题上特别好用，一般无向图上的问题也可以先搬到树上做~~骗部分分~~，然后拓展到一般无向图上。

重要性质：无向图的 dfs 树上只有树边和返祖边。

CF1364D Ehab's Last Corollary

点此看题

~~但凡删掉找出环的问我就不会做了~~

dfs 树上找最小环是容易的，直接解决 $2$ 问。

如果树上最小的环 $\geq k$，把它取出来直接构造独立集即可。

P5811 [IOI2019] 景点划分

点此看题

不妨设 $a\le b \le c$，此时 $a\le \dfrac{n}{3},b\le \dfrac{n}{2},b\le n-2a$。

构造更大连通块严格强于较小的，方案只用使 $A/B$ 联通。

把问题放到 dfs 树上弱化~~进行拿 22pts 活动~~，一个 naive 的想法是枚举一棵子树把它划分给 $A$ 判断是否合法，判定条件是较小的一边 $\geq a$，另一边 $\geq b$，注意到划分给 $B$ 的子树一定包含重心。

拓展到图上，先跑一遍上面的构造，如果没有合法方案，去掉重心和与它相连的边，此时每一棵子树大小都 $< a$。

将重心上方的子树称为 $T$，下方的子树按照遍历顺序分别称为 $S_i$。

无向图 dfs 树上非树边只有返祖边的性质终于要出场了，根据它得到不同的 $S_i$ 之间没有非树边直接相连，且 $S_i$ 只与 $T$ 之间有非树边直接相连。

我们把 $T$ 划分给 $A$，不够的部分我们让它们通过返祖边与 $T$ 相连,只要我们不把重心划分给 $A$，$B$ 就可以通过重心联通。

依次把所有与 $T$ 通过返祖边相连的 $S_i$ 加入 $A$ 直到 $|A|\geq a$，因为 $|S_i|<a$ 且最后一棵子树加入前 $|A|<a$，所以最终 $|A|< 2a$，剩下的连通块大小 $\geq n-2a$，满足 $B$ 的大小限制。

$\mathcal{Part}\ 3$ 归纳法

抽象至极

理论上是通过构造更小范围和边界 $n=1$ 上的解缩小问题的范围，需要注意转化为更小的范围时不要丢掉题目中的性质。

~~实际上是我根本想不到怎么缩小范围。~~

题目可能给出了一个限制，只要时刻满足这个限制就可以保证构造正确。

还有就是往往这种题有一个简单~~往往并不显然~~的无解条件或者根本就没有无解情况，应用归纳法可以让构造的过程和证明无解条件的充要性同时进行。

猜就完了！

CF1470D Strange Housing

点此看题

直接构造时一个操作对后边决策影响很大，考虑归纳。

无解当且仅当不连通。

$n=1$ 显然联通。

维护一个点集，初始只有一个点，染成黑色，每次加入一个与点集内点联通的点，如果与它直接相连的点有黑色则染白，否则染黑。

构造每时每刻都保证了联通性，归纳可得一定有解。

CF1515F Phoenix and Earthquake

点此看题

猜一下，无解当且仅当 $\sum a\le (n-1)x$ 或不连通。

满足以上限制时规模 $n=2$ 为边界可以直接缩。

最后的缩过的边肯定是一棵树，掏出无向图的 dfs 树，每条边表示会在某时刻缩掉两侧的点。

拿出一个叶子 $u$，如果 $a_u\geq x$ 则缩点，转化为 $n-1$ 规模的问题；否则先不管它，问题规模缩小 $1$，且此时的问题仍然满足 $\sum a\le (n-1)x$ ，解决完剩下 $n-1$ 规模的问题再来搞它即可。

ARC122E Increasing LCMs

点此看题

序列合法的充要条件：$\forall i,\gcd(\operatorname{lcm}_{j<i}\{a_j\},a_i)<a_i$。

$n=1$ 显然满足。

每次放序列最后面的数从而缩小规模到 $n-1$，因为 lcm 单增，$a_i$ 一定会在某时刻 $t$ 加入符合条件的集合 $S$ 后不再退出，每次取任意 $a_i\in S$ 放在序列最后，如果 $S=\emptyset $ 则无解。

~~像不像倒序构造~~

注意到 $\gcd(\operatorname{lcm}_{j<i}\{a_j\},a_i)<a_i \Leftrightarrow \operatorname{lcm}_{j\neq i}\{\gcd(a_j,a_i)\}<a_i$，后者可以在构造同时维护。

时间复杂度 $\mathcal{O}(n^3\log n)$。

Baggage

归纳法同样适用于一些要求构造最少操作次数的方案的题目。

通用套路是找出答案的显然下界（通过搜索、随机化打表等方法），然后归纳证明充分性。

点此看题

打表发现最小操作次数为 $n$。

先证必要性，记 $d$ 为序列中相邻的颜色相同对的个数，初始态 $d=0$，终止态 $d=2n-2$，每次操作最多使 $d$ 增加 $2$，特殊地，第一次操作只会使 $d$ 增加 $1$，综上总操作次数至少为 $1+\left \lceil \dfrac{2n-3}{2} \right \rceil =n$。

注意到一次操作移动的对只有两种：颜色不同的和颜色相同的。

为了达到下界，除第一次外每次移动都必须使 $d$ 增加 $2$，那么移动二类对时终点一定是两对和它颜色一样的二类对包夹的长为 $2$ 的空位，并且由于无论任何操作都不会破坏已经构造好的相邻同色对，开始移动二类对之前局面一定形如下图

\[ABBAABBAA...AA\_\ \_AA...BBAAB \]

空位在中间的某两个相邻的位置，这个局面下容易通过移动 $\left \lfloor \dfrac{n}{2} \right \rfloor$ 次二类对构造出最终方案。

现在问题转变为如何通过移动一类对在 $\left \lfloor \dfrac{n}{2} \right \rfloor$ 内构造以上局面。

归纳法，先把 $n\le 7$ 的情况给搜出来。

手玩一下可以用下图的方式递归

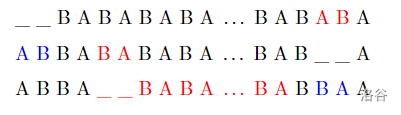
江莉那里盗的图

~~构造也不全是分析，还是需要人类智慧的~~

一次递归用 $2$ 次操作缩减到 $n-4$，一共会用 $\left \lfloor \dfrac{n}{2} \right \rfloor$ 次。

至此构造完毕。

$\mathcal{Part}\ 4$ 构造图

图可以简单地表示一些关系和限制，转化为图论问题可以避免抽象地思考。

有向边：转化、偏序。

无向边：匹配。

环、团、独立集：有一些特定关系的集合。

特殊的图它与众不同的地方可能就是构造的答案：基环树的环。

待更，遇到了再回来写。

CF1270G Subset with Zero Sum

点此看题

化一下柿子，把与 $i$ 相关地放在一起作为元素 $i$ 的属性 $i-n\le a_i \le i-1 \Leftrightarrow 1 \le i-a_i\le n$，好看多了。

明示连边了已经，建立有向图，连接 $i \rightarrow i-a_i$，每个点出度均为 $1$，建出来的一定是内向基环树森林，更好看了，把长得最乖的环拿出来发现把环上的 $a_i$ 丢进集合一定符合条件。

为什么呢？

~~这是构造题不要问为啥，猜就完了~~

环上有 $\sum i=\sum i-a_i$，移项变成 $\sum a_i=0$。

CF1404D Game of Pairs

构造要求和为 $x$ 倍数的可以在 $\bmod\ k$ 及 $k$ 的某些特殊因子的意义下做。

点此看题

小 A 的方案需要尽可能地控制小 B 能够选到的数 $\bmod\ 2n$ 意义下的结果。

有一个 naive 的想法是直接把 $\bmod\ n$ 相同的一对数组成一个 pair，这样后手无论怎么选在 $\bmod\ n$ 意义下总为 $\sum_{i=1}^{n} i$，当 $2|n$ 时 $\sum_{i=1}^{n} i\equiv \dfrac{n}{2} (\bmod\ n)$，符合条件。

否则当 $2\nmid n$ 时， $\sum_{i=1}^{n} i\equiv 0 (\bmod\ n)$，而所有数总和 $\sum_{i=1}^{2n} i\equiv n (\bmod\ 2n)$，这意味着小 B 通过在所有 $\bmod\ n$ 意义下的剩余系中任取一个构造出的方案如果不满足 $\sum i\equiv 0 (\bmod\ 2n)$ 的话，它的补集一定满足条件。

猜测 $2\nmid n$ 时小 B 总能在所有 $\bmod\ n$ 同余的两数中取任意一个从而取胜，无向图独立集可以表示在一对数中最多取一个的限制，在 $(i,i+n)$ 以及小 A 给出的对之间建边，得到一个边数、点数均为 $2n$ 且每个点的度均为 $2$ 的图，意味着这张图是由若干个不相交的环构成的。

这张图上大小为 $n$ 的独立集不难通过黑白染色构造。