GNN学习 GNN Layer(持续更新中)
GNN学习 GNN Layer
GNN的通用框架
- 1.对GNN的一个网络层进行信息转换和信息聚合两个操作
- 2.连接GNN的网络层
- 3.图增强,分为图特征增强和图结构增强
- 4.学习目标,有监督学习还是无监督学习,节点/边/图级别
1.信息转换和信息聚合
GNN Layer=Message+Aggregation
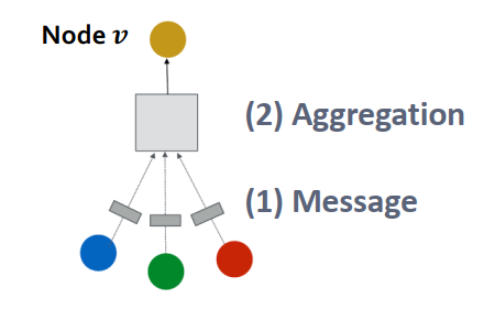
不同的实例有不同的信息转换和增强的方法
GNN单层网络的目标是将一系列向量压缩到一个向量中
Message computation
\(m_u^l=MSG^l(h^{l-1}_u)\)
每个节点都会产生信息,这些信息将会被传递到其它节点
MSG可以是一个矩阵W
Message Aggregation
\(h_v^l=AGG^l({m_u^l,u\in N(v)})\)
每个节点都要聚合从其它的邻居节点处获得的信息
AGG可以是Sum,Mean或者Max
存在的问题:
会导致节点自身的信息丢失,因为在计算时不会包含节点本身,解决方法就是在计算\(h_v^l\)时包含\(h_v^{l-1}\)
- 在信息传递时,对节点本身和邻居应用不同的权重矩阵
- 在信息聚合时,将邻居节点与自身信息进行聚合
\(m_u^l=W^lh^{l-1}_u\)
\(m_v^l=B^lh^{l-1}_v\)
\(h_v^l=CONCAT(AGG({m_u^l,u\in N(v)}),m_v^l)\)
所以一个单层的神经网络就是将这些东西结合在一起
- Message:\(m_u^l=MSG^l(h^{l-1}_u),u\in {N(v)\cup v}\)
- Aggregation:\(h_v^l=AGG^l(\{m_u^l,u\in N(v)\}),m_v^l)\)
在做完前面的步骤之后,我们可以将其经过一个非线性激活函数\(\sigma\),例如ReLU或者Sigmoid
经典案例分析
1.GCN
前面讲到的GCN的传递函数
\(h_v^l=\sigma(\sum_{u\in N(v)}W^l\frac{h_u^{l-1}}{\left | N(v) \right | })\)
累加号就是聚合的过程
累加号后面的就是信息传递的过程
详细来说:
Message:
\(m_u^l=\frac{1}{|N(v)|}W^lh^{l-1}_u\)
Aggregation:
\(h^l_v=\sigma(Sum(\{m_u^l,u\in N(v)\}))\)
2.GraphSAGE
这个方法包含了节点本身的一些信息
\(h_v^l=\sigma(W^l\cdot CONCAT(h_v^{l-1},AGG(\{h_u^{l-1},\forall u\in N(v)\})))\)
Message过程在AGG里进行计算了
先聚合邻居节点,再聚合自身节点
AGG可以是Sum,Mean甚至是LSTM
之后要进行归一化,我们这里采用L2 Normalization
对每层都进行L2归一化,也就是
\(h_v^l\leftarrow \frac{h_v^l}{||h_v^l||} \forall v\in V\)
并且\(||u||_2=\sqrt{\sum_iu_i^2}\)所以被称为L2-norm
3.GAT(Graph Attention Network)
层之间的传递公式为
\(h_v^l=\sigma(\sum_{u\in N(v)}\alpha_{vu} W^lh_u^{l-1})\)
其中\(\alpha_{vu}\)被称为注意权重(attention weight)
例如GCN里\(\alpha_{vu}=\frac{1}{|N(v)|}\)
GAT
如何学习\(\alpha_{vu}\)
目标:确定图中每个节点的不同邻居的重要性
想法:
- 节点关注邻居的信息
- 间接的确定邻居不同节点的不同的权重
注意力机制
\(\alpha_{vu}\)是作为注意力机制a的副产品被计算的
首先计算两个节点之间传递信息的注意力系数\(e_{vu}\)
\(e_{vu}=a(W^lh_u^{l-1},W^lh_v^{l-1})\)
注意力系数表示了从节点u传递给节点v的信息的重要性
之后我们对注意力系数归一化,得到注意力权重,这里可以采用softmax来进行归一化
那么注意力机制的形式是什么
我们可以用简单的单层神经网络来作为注意力机制a
那么相当于
\(e_{vu}=Linear(W^lh_u^{l-1},W^lh_v^{l-1})\)
也可以引入多头注意力机制
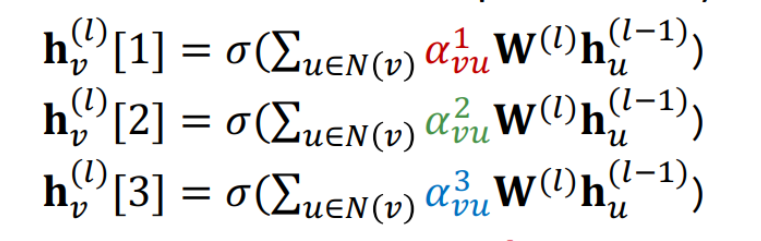
最后对输出进行聚合
\(h_v^l=AGG(h_v^l[1],h_v^l[2],h_v^l[3])\)
注意力机制的主要好处就是确定不同邻居节点的不同重要性
A对B的注意力和B对A的注意力可以不同
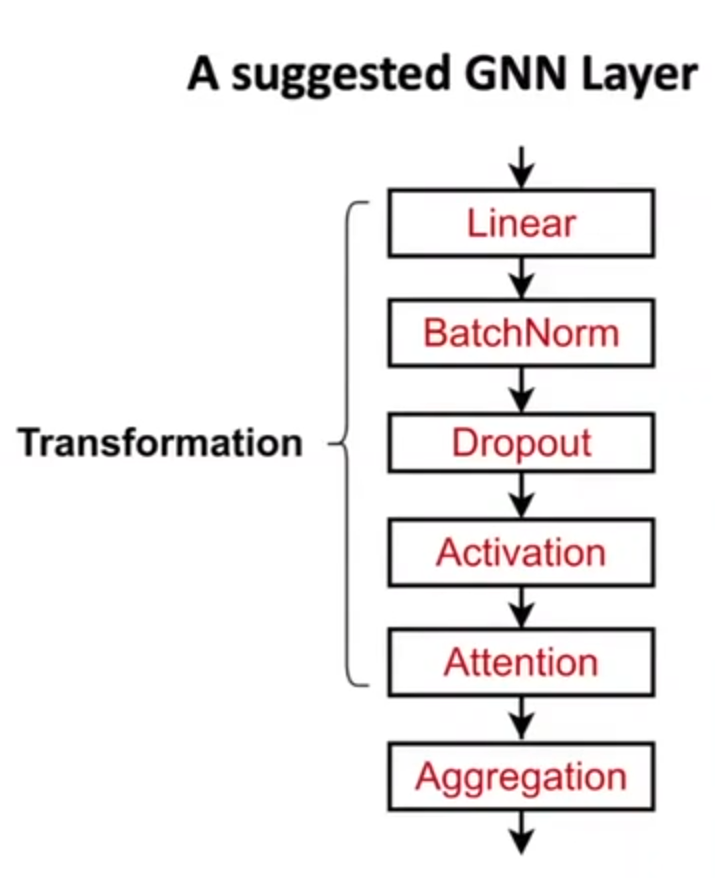
实际的GNN Layer搭建如下