2023 年 7 月训练记录

zhaohaikun / 2023-07-21 / 原文

训练

7 月没有做题题题题题题题题题。

MdOI R5 Many Minimizations

原问题有个经典做法，首先考虑暴力 DP，\(f_{i,j}\) 表示第 \(i\) 个数 \(=j\) 的最小代价，不难发现 DP 值是个分段函数，然后考虑用堆来维护。

设 \(mn_i=\min_{j}\{f_{i,j}\}\)，每次操作相当于是往堆中先加入两个 \(a_i\)，然后弹出最大值 \(mx\)，可以发现 \(mn_i=mn_{i-1}+mx-a_i\)。

于是，我们发现当 \(a_i<mx\) 时才会有贡献。计算答案时，我们对每个 \(a_i\le t< mx\) 分开计算，不难发现，\(t\) 的个数 \(= mx-a_i\)。

我们把 \(a_i< x\) 的设为 \(0\)，将 \(a_i\ge x\) 的设为 \(1\)，则就相当于是一个函数 \(g_i\) 表示堆内 \(1\) 的个数。

当 \(0\) 加入时：
1. 若 \(g_{i-1}>0\)，则答案增加 \(1\)；
2. 若 \(g_{i-1}=0\)，则答案不变。
  换而言之，\(g_{i}=\max(0,g_{i-1}-1)\).
当 \(1\) 加入时：
\(g_{i}=g_{i-1}+1\)。

我们发现对 \(0\) 取 \(\max\) 的操作，是我们比较难处理的。

我们把 \((i,g_i)\) 看成一个点。我们考虑将对 \(0\) 取 \(\max\) 的位置都先整体向上平移，并要求平移后的路径至少有一个点在 \(x\) 轴上，这个限制我们可以通过 \(y\) 坐标全部 \(\ge 0\) 的方案数减去 \(y\) 坐标全部 \(\ge 1\) 的方案数来处理，计算后面的东西可以使用反射容斥来算。

对于 \((0,a)\) 出发，到 \((n,b)\) 结束的路径，我们考虑计算它对答案。首先，总的下降次数为 \(\frac{n+a-b}{2}\)，而由于对 \(0\) 取 \(\max\) 的位置不对答案产生贡献，所以贡献为 \(\frac{n+a-b}{2}-a=\frac{n-a-b}{2}\)。

时间复杂度 \(O(n^2)\)。

记录。

AGC015E Mr.Aoki Incubator

我们先把点按坐标排序，一个点 \(i\) 被选中后，能染色在它右侧速度小于 \(\max\limits_{j=1}^{i} v_j\) 的点，以及在它左侧速度小于 \(\max\limits_{j=i}^{n} v_j\) 的点。

所以，越左的点对其左侧影响能力越强；越右的点对其右侧影响能力越强。于是，我们考虑 DP，\(f_i\) 表示 \(i\) 被选中，且 \([1,i]\) 已经全部被染色。因为越左的点对其左侧影响能力越强，如果前 \(i\) 个确定了，并且第 \(i\) 个被选中了，还有点没被染色，则说明右侧再怎么选也不可能让左侧的点被染色。

对于 \(f_i\)，可行的转移 \(j\) 是一段连续的区间，因为要求 \(j\) 和 \(i\) 染色能覆盖内部的所有点，所以 \(j\) 越大，对其右侧影响能力越强，且区间更小，所以更优。

考虑使用双指针来维护最左的可行转移 \(j\)，并用前缀和求出答案。

时间复杂度 \(O(n\log n)\)，瓶颈在于排序。

记录。

P2762 太空飞行计划问题

最大权闭合子图的板子。

我们让 \(S\) 向所有点权为正的点连边，流量为点权，让所有点权为负的点向 \(T\) 连边，流量为 \(-\) 点权，原图上的边流量为 \(\infty\)。

正确性：答案为所有正点权和 \(-\) 最小割。首先，最小割不会割原图的边，割 \(S\) 到正点权点的边相当于不选这个点，割负点权的点到 \(T\) 的边，相当于选了一些正点权的点并由于原题的限制一定要选这个点，导致选了这个点。

构造方案就是 \(S\) 能到的点。

记录。

[TJOI2015] 弦论

由于对 SAM 的不熟悉（主要还是因为 \(10\) 级就开摆了），再加上我构造法没学明白，导致我一直不会后缀树，然后模拟赛考了。

不过强大 Qiuly、ybw051114 告诉我 SA 也可以建后缀树，于是就来学了下。

source。

我们先对原串进行后缀排序，然后求出 \(height\)。我们现在处理区间 \([l,r]\)，找到区间中 \(height\) 最小的位置，将区间分裂，一直递归下去即可得到一棵后缀树。

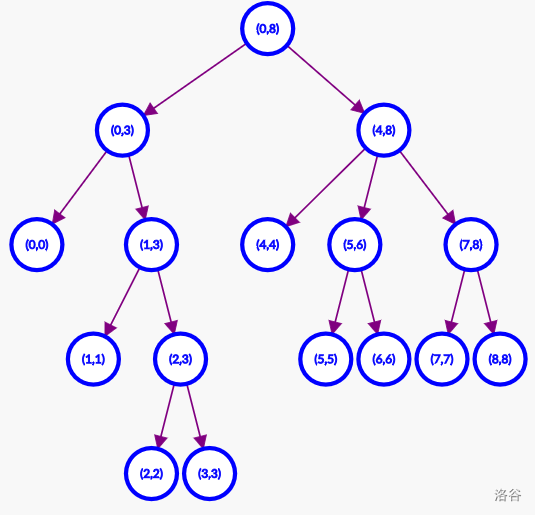
板子：

int build(int fa, int l, int r) {
	int num = ++tot;
	::l[num] = l, ::r[num] = r;
	L[num] = R[fa] + 1;
	if (l == r) {
		pos[l] = num;
		R[num] = n - sa[l] + 1;
		return num;
	}
	int pos = qry(l + 1, r);
	R[num] = height[pos];
	ls[num] = build(num, l, pos - 1), rs[num] = build(num, pos, r);
	return num;
}

感觉这比构造法好理解太多了！！！

有了后缀树做这题就很简单了。

对于 \(t=0\) 的问题：我们先后缀排序，然后从前往后每个后缀的 \([height_i+1,len_i]\) 的前缀就是按照字典序排好的所有本质不同子串。

对于 \(t=1\) 的问题：我们按照上面的方法把后缀树建出来，然后我们在后缀树上遍历一下就可以求出答案了。