Competition Set - 在线赛

by-chance / 2023-07-21 / 原文

一些 Online Judge 上的比赛。

HDU多校赛第二场

2023-7-20

1001 Alice Game

一段长为 $n$ 的序列，两人轮流操作。每次操作，可以选取序列中一段长为 $k$ 且不在两端的区间，将其删掉，得到两个新的序列。也可以直接删掉一个长度不超过 $k$ 的序列。不能操作者判负。问谁必胜。

$0\le n \le 10^9,2\le k \le 10^7$。

Solution：我不知道。虽然这个题是我写的，而且一发就过了，但是我在写题解时发现自己的结论是错的。

后来看了官方题解，答案是当且仅当 $n \bmod (4k+10)==k+1$ 时后手胜。而我的条件是 $n \bmod (4k+2)==k+1$ 或 $4k+2 | n$。所以这个代码怎么过的呢？

1005 Or

给定两个长为 $n$ 的序列 $a,b$，$m$ 组询问 $l,r$，求 $\oplus_{i=l}^{r} \oplus_{j=i}^{r}(a_i+\sum_{k=i+1}^{j}b_k)$。只用输出 $\sum_{i=1}^{m} ans_i \times 233^i \bmod 998244353$，这里
$ans_i$ 表示第 $i$ 组询问的答案。

$1\le n \le 10^5,1\le m \le 10^6,0\le a_i \le 5\times 10^8,0\le b_i \le 5000$。

Solution：按位处理。试图找出 $a_i$ 要加 $b_j$ 到哪里在能使这一位有 $1$。然后用一个 ST 表就可以解决问题。

先换成前缀和的形式，用 $b_i$ 表示实际的 $b$ 的前 $i$ 项和，$a_i-b_i+2^{30}$ 代替 $a_i$，则新的 $a_i+b_j$ 在 $j \ge i$ 时就可以代表原来的 $a_i+\sum_{k=i+1}^{j} b_j$。

要使得 $a_i$ 与某个 $b_j$ 相加，第 $k$ 位是 $1$，则需要 $a_i$ 与 $b_j$ 的第 $k$ 位相同，且更低位相加进位；或者第 $k$ 位不同，且更低位相加不进位。那么对所有低位离散化，建线段树，在每个权值上记下最小下标。扫到 $a_i$ 时二分查找可用的区间即可。我开了两棵线段树来解决，实际可以不用。

#include<bits/stdc++.h>
#define RE register
using namespace std;
inline int read(){
    int x=0;char ch=getchar();
    while(ch<'0'||ch>'9')ch=getchar();
    while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
    return x;
}
const int N=1e5+5,M=1e6+5,base=233,P=998244353,INF=2147483647;
int T,n,m,a[N],b[N],x[N],nxt[N],st[N][20],q[M][2],ans[M];long long res;
#define ls p<<1
#define rs p<<1|1
#define mid ((l+r)>>1)
int mn[N<<2];
inline void modify(int p,int l,int r,int x,int v){
    if(l==r){mn[p]=v;return;}
    if(x<=mid)modify(ls,l,mid,x,v);
    else modify(rs,mid+1,r,x,v);
    mn[p]=min(mn[ls],mn[rs]);
}
inline int query(int p,int l,int r,int L,int R){
    if(l>=L&&r<=R)return mn[p];
    int res=INF;
    if(L<=mid)res=min(res,query(ls,l,mid,L,R));
    if(R>mid)res=min(res,query(rs,mid+1,r,L,R));
    return res;
}
int main(){
    T=read();
    while(T--){
        n=read();m=read();res=0;
        for(RE int i=1;i<=n;++i)a[i]=read();
        for(RE int i=1;i<=n;++i)b[i]=b[i-1]+read();
        for(RE int i=1;i<=n;++i)a[i]=a[i]-b[i]+(1<<30);
        for(RE int i=1;i<=m;++i){q[i][0]=read();q[i][1]=read();ans[i]=0;}
        for(RE int k=0;k<30;++k){
            int C=(1<<k)-1;
            for(RE int i=1;i<=n;++i)x[i]=b[i]&C;
            sort(x+1,x+n+1);int t=unique(x+1,x+n+1)-x-1;
            for(RE int i=1;i<=n;++i)nxt[i]=INF;
            for(RE int i=1;i<=t*4;++i)mn[i]=INF;
            for(RE int i=n;i>=1;--i){
                int y=lower_bound(x+1,x+t+1,b[i]&C)-x;
                if((b[i]>>k)&1)modify(1,1,t,y,i);
                int val=C-(a[i]&C);
                int p1=upper_bound(x+1,x+t+1,val)-x-1,
                    p2=lower_bound(x+1,x+t+1,val+1)-x;
                if(p1>=1)p1=query(1,1,t,1,p1);else p1=INF;
                if(p2<=t)p2=query(1,1,t,p2,t);else p2=INF;
                if(!((a[i]>>k)&1))nxt[i]=min(nxt[i],p1);
                else nxt[i]=min(nxt[i],p2);
            }
            for(RE int i=1;i<=t*4;++i)mn[i]=INF;
            for(RE int i=n;i>=1;--i){
                int y=lower_bound(x+1,x+t+1,b[i]&C)-x;
                if(!((b[i]>>k)&1))modify(1,1,t,y,i);
                int val=C-(a[i]&C);
                int p1=upper_bound(x+1,x+t+1,val)-x-1,
                    p2=lower_bound(x+1,x+t+1,val+1)-x;
                if(p1>=1)p1=query(1,1,t,1,p1);else p1=INF;
                if(p2<=t)p2=query(1,1,t,p2,t);else p2=INF;
                if((a[i]>>k)&1)nxt[i]=min(nxt[i],p1);
                else nxt[i]=min(nxt[i],p2);
            }
            for(RE int i=1;i<=n;++i)st[i][0]=nxt[i];
            for(RE int j=1;(1<<j)<=n;++j)
                for(int i=1;i<=n-(1<<j)+1;++i)
                    st[i][j]=min(st[i][j-1],st[i+(1<<j-1)][j-1]);
            for(RE int i=1;i<=m;++i){
                int l=q[i][0],r=q[i][1],x=log2(r-l+1);
                if(min(st[l][x],st[r-(1<<x)+1][x])<=r)ans[i]|=(1<<k);
            }
        }
        for(RE int i=m;i>=0;--i)res=(res*base%P+ans[i])%P;
        printf("%lld\n",res);
    }
    return 0;
}

1007 foreverlasting and fried-chicken

给定一个点数为 $n$ 的图，求如图所示的子图数目。

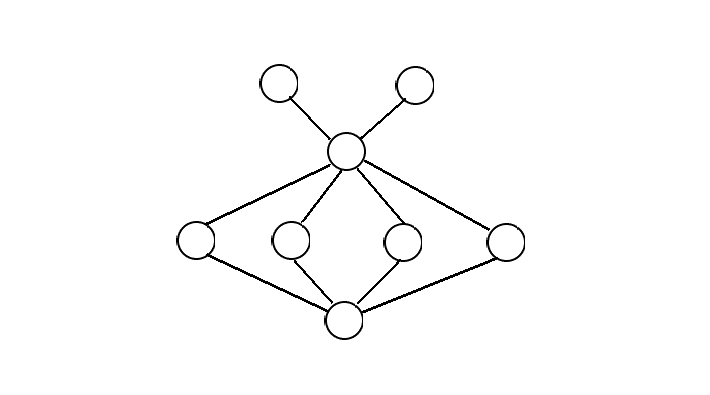
$1\le n \le 1000, \sum n \le 3000$。

Solution：枚举度为 $4$ 和 $6$ 的两个点，用 bitset 求交，然后做一个简单的计数。注意这两个点之间的边不能计入。复杂度有点悬，但能过。

1008 Hello World 3 Pro Max

长为 $n$ 的字符串中，$h,e,l,o,w,r,d$ 每个字符有一个出现概率。有 $m$ 次修改和询问操作，修改为确定某个位置，询问为问一个区间的字符串中子序列 $helloworld$ 的期望数。

$1\le n,q\le 5 \times 10^4$。

Solution：DDP板子。我写了，队友卡卡常过了。然后就是正解？

洛谷 7 月月赛 III

2023-7-15

A 浴眼盯真 [过水已隐藏]

B 众数 I

给定一个长度为 $n$ 的序列 $a$，我们通过以下方式构造序列 $b$：

初始时 $b=a$。
依次对 $b$ 进行 $k$ 次操作，每次操作选择任意一个元素并将其修改为任意整数。

求出有多少整数可能成为 $b$ 的众数。注意众数可以有多个。

$1\leq n\leq 10^6$，$0\leq k\leq n $，$1\leq a_i\leq n$。

Solution：贪心。尝试某个位置能否成为众数，那么肯定要把比它出现次数多的数都减小，加到它上面。所以我们处理出出现次数不少于 $k$ 的数的个数，然后一层层减掉，减到 $0$ 为止。如果此时停下的位置 $c$ 不超过 $k$ 则无穷多组解，否则解数为出现次数不少于 $c-k$ 的数的个数。

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
int n,k,a[N],b[N],c,t,ans;
int main(){
    scanf("%d%d",&n,&k);t=k;
    for(int i=1,x;i<=n;i++){scanf("%d",&x);a[x]++;}
    for(int i=1;i<=n;i++)b[a[i]]++;
    for(int i=n;i>=1;i--)b[i]+=b[i+1];
    for(int i=n;i>=1;i--){
        if(t>=b[i])t-=b[i];
        else{c=i;break;}
    }
    if(c<=k){printf("pigstd\n");return 0;}
    printf("%d\n",b[c-k]);
    return 0;
}

C 众数 II

给定一个长度为 $n$ 的序列 $a$，我们通过以下方式构造序列 $b$：

初始时 $b$ 为空序列。
对于 $i=1,2,\cdots,n$，我们依次向 $b$ 的尾部插入 $1,2,\cdots,a_i$。

求出 $b$ 的每个子区间的最小众数的和对 $998244353$ 取模后的值。
$1\leq n\leq 10^6$，$1\leq a_i\leq 10^6$。

Solution：把每一个 $a_i$ 构造出的 $1,2,\cdots,a_i$ 称为一个段。注意到，如果一个子区间的最小众数是 $x \ne 1$，那么必定满足三个条件：第一，区间以 $x$ 开头；第二，区间经过的段都包含 $x$；第三，该区间包含结尾的段的 $x$。

那么，对于一段 $a_i,\cdots,a_j$，假设它是一个极长的，所有数都不小于 $x$ 的区间，那么它对最小众数是 $x$ 的段的数目贡献为

\[\sum_{i\le l\le r\le j}(a_r-x+1)=\sum_{i\le y\le j}(y-i+1)a_y-\frac{1}{2}(i-j+1)(i-j+2)(x-1) \]

从大到小维护 $x$，维护若干连续段。加入一个点可能引起若干区间的合并。减少 $x$ 时答案也会增加一个值（当前的子区间数），可以顺便维护。注意 $x=1$ 的情况比较麻烦（比如可能不以 $1$ 开头），所以求出所有 $x \ne1$ 的情形后用总的减掉即可。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e6+5,P=998244353;
int n,a[N],id[N],t[N],m;ll ans,cnt0,cnt,tot;
struct node{int l,r;ll sum,sum2;}r[N];
ll f(node x,int y){return (x.sum2-1ll*(x.r-x.l+2)*(x.r-x.l+1)/2%P*(y-1)%P+P)%P;}
bool cmp(int i,int j){return a[i]==a[j]?i<j:a[i]>a[j];}
void merge(int d,int i){
    node x=r[t[d-1]],y=r[t[d]],z;
    t[y.r]=t[x.r];z.l=x.l;z.r=y.r;
    z.sum=(x.sum+y.sum)%P;
    z.sum2=(x.sum2+y.sum2+1ll*(x.r-x.l+1)*y.sum%P)%P;
    cnt0=(cnt0+1ll*(x.r-x.l+1)*(y.r-y.l+1)%P+P)%P;
    cnt=(cnt-f(x,i)-f(y,i)+f(z,i)+2*P)%P;r[t[z.l]]=z;
}
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        scanf("%d",a+i);id[i]=i;
        tot=(tot+a[i])%P;
    }
    tot=tot*(tot+1)/2%P;
    sort(id+1,id+n+1,cmp);
    for(int i=1000000,p=1;i>=2;--i){
        cnt=(cnt+cnt0)%P;
        while(a[id[p]]==i){
            int x=id[p];
            t[x]=++m;r[m]={x,x,a[x],a[x]};
            ++cnt0;++cnt;
            if(a[id[p]-1]>=i)merge(id[p],i);
            if(a[id[p]+1]>i)merge(id[p]+1,i);
            ++p;
        }
        ans=(ans+cnt*i%P)%P;
        tot=(tot-cnt+P)%P;
    }
    printf("%lld\n",(ans+tot)%P);
    return 0;
}

D 中点

交互题。一棵 $n$ 个点的树，边权为 $1$，可以询问两个点的中点（若不存在返回 $0$），请通过不超过 $147154$ 次询问得到树的形态。

$2\le n \le 10000$。

Solution：以 $1$ 为根，首先试图确定一条与根相邻边。我们询问所有点与 $1$ 的中点，找到可以取中点次数最大的那个点，它所取的最后一次中点的结果一定与 $1$ 相邻。

证明：熟知对任何正整数 $n$，$1,2,\cdots,n$ 中 $2$ 的幂次最高的数一定是 $2$ 的方幂。能取中点的次数就是深度中 $2$ 的幂次，而是 $2$ 的方幂意味着取完中点后的深度为 $1$，即相邻。

然后来确定所有点的深度。设已知 $1$ 与 $p$ 相邻，再询问所有点与 $p$ 的中点。如果点 $x$ 与 $1$ 的中点为 $y$，则 $d_x=2d_y$；如果点 $x$ 与 $p$ 的中点为 $y$，则 $d_x=2d_y \pm 1$，其中 $x,y$ 在 $p$ 的子树内时取负号，在 $p$ 的子树外时取负号。可以写一个拓扑排序来实现。

最后确定每个点的父亲。深度为 $1$ 的点已经确定。对深度为 $k$ 的点 $u$，我们随便取一个深度为 $k-2$ 的点 $v$，不断令 $v$ 变成 $u,v$ 的中点，直到 $v$ 的深度为 $k-1$，此时 $v$ 就是 $u$ 的父亲。如果中途某次 $u,v$ 不能取中点，就让$v$ 变成 $v$ 的父亲继续找。正确性在于第一次操作后 $v$ 就一定在 $u$ 到根的路径上了。

操作次数上界是 $2n+\sum_{k=1}^{n} \lceil \log_2 k \rceil$，能过。

#include<bits/stdc++.h>
using namespace std;
const int N=10006;
int id,n,c[N][2],m;
int a[N],deg[N],f[N],lst[N],p;
int b[N],dep[N],g[N],fa[N],d,st;
void query(int u,int v,int&r){
    cout<<"? "<<u<<" "<<v<<endl;
    fflush(stdout);
    cin>>r;
    if(r==-1)exit(0);
}
void ans(int u,int v){c[++m][0]=u;c[m][1]=v;}
queue<int> Q;vector<int> son[N];
int main(){
    cin>>id>>n;
    for(int i=2;i<=n;i++)query(1,i,a[i]);
    for(int i=2;i<=n;i++)if(a[i])deg[a[i]]++;
    for(int i=2;i<=n;i++)if(!deg[i])Q.push(i),f[i]=0;
    while(!Q.empty()){
        int u=Q.front(),v=a[u];Q.pop();
        --deg[v];f[v]=max(f[v],f[u]+1);
        if(!deg[v])Q.push(v);
    }f[0]=-1;
    for(int i=2;i<=n;i++)if(f[i]>f[p])p=i;dep[p]=1;
    for(int i=2;i<=n;i++)if(i!=p)query(i,p,b[i]);
    for(int i=2;i<=n;i++)if(i!=p){
        if(a[i]!=p)son[a[i]].push_back(i);
        if(b[i]!=1)son[b[i]].push_back(i);
        if(a[i]==p)dep[i]=2,Q.push(i),g[i]=1;
        if(b[i]==1)dep[i]=1,Q.push(i),g[i]=2;
    }
    while(!Q.empty()){
        int u=Q.front();d=max(d,dep[u]);Q.pop();
        for(int v:son[u]){
            g[v]=g[u];
            if(u==a[v])dep[v]=dep[u]*2;
            else{
                if(g[v]==1)dep[v]=2*dep[u]-1;
                else dep[v]=2*dep[u]+1;
            }
            Q.push(v);
        }
    }
    for(int i=1;i<=n;i++)if(dep[i]==1)ans(1,i),fa[i]=1;
    for(int i=2;i<=d;i++){
        for(int j=1;j<=n;j++)if(dep[j]==i-2)st=j;
        for(int u=1;u<=n;u++)if(dep[u]==i){
            int v=st,w;
            while(dep[v]!=i-1){
                query(u,v,w);
                if(w==0)v=fa[v];
                else v=w;
            }
            ans(u,v);fa[v]=u;
        }
    }
    cout<<"!"<<endl;fflush(stdout);
    for(int i=1;i<n;i++){
        cout<<c[i][0]<<" "<<c[i][1]<<endl;
        fflush(stdout);
    }
    return 0;
}