拟合
目的:
确定一条线或一个圆一个圆心的方程
面临的问题:
在线上的点因为噪声偏离这条线。
其他线上的点(外点)影响这条线的拟合。
遮挡导致这条线的不连续。
总括
所有的点都属于这条线:最小二乘
有外点:RANSAC,鲁棒拟合
有好多其他的线:RANSAC,或则霍夫变换
最小二乘

最小二乘面临的问题:
- 如果直线垂直(可以认为垂直于x轴)没法描述点到线的纵向距离
- 原本不垂直的点可能经过图像的旋转变成垂直的点
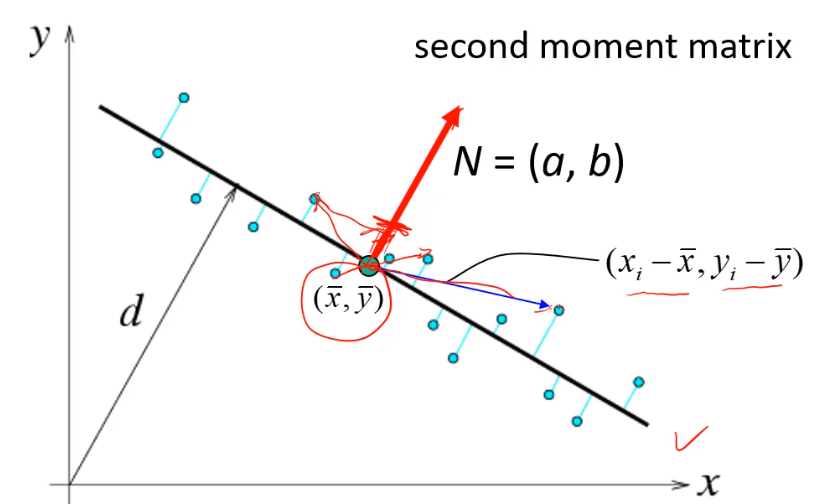
全最小二乘法
为解决上述问题我们使用全最小二乘法,即让点到线之间的距离最小


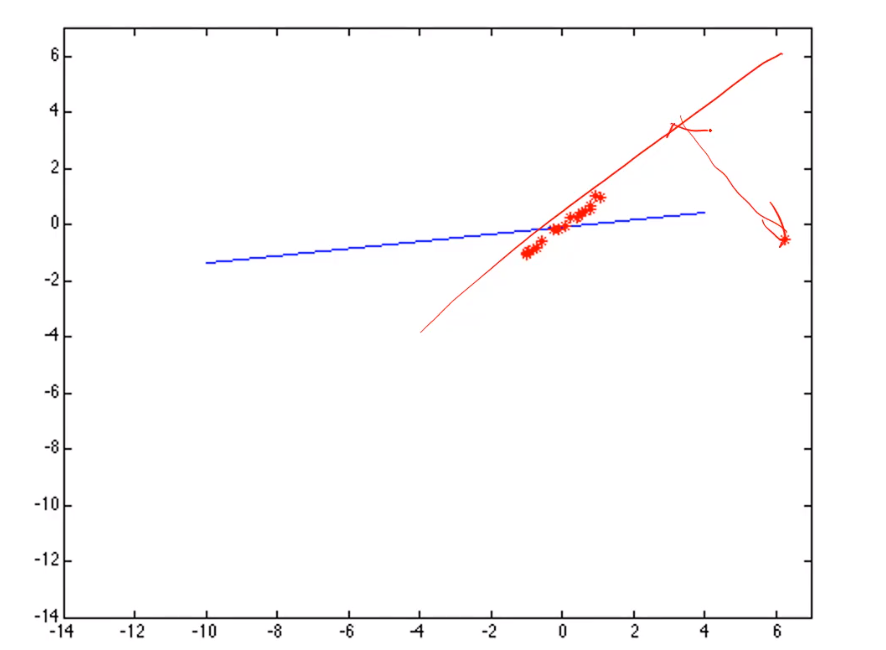
两个最小二乘的缺陷:
如下图所示,为了照顾外点(也就是那个偏离程度最大的点)必须拟合成红色的线,这会造成和蓝色的线有很大的偏差。
鲁棒的最小二乘:

此时E变成了非线性优化问题(看ρ的表达式),那么我们可以使用最优化的方法求解,我们可以使用全最小二乘法作为鲁棒的最小二乘法的初值。
鲁棒的最小二乘法问题:
σ太小极端情况所有点的距离都被看成1了,σ太大又变成上面的最小二乘问题了。一般取1.5倍的平均残差(残差就是点到线的距离)