模拟赛T3T4题解
T3:
考虑对每个人分开处理,f[i][j][0/1]表示已经做了A本语文作业,B本数学作业,目前在做语文/数学,需要的最小时间。
转移形如:\(f[i][j][s]=min{f[i-l][j][1-s]+K\times{l^2}+B}\) 非常典的斜优或者决策单调性。决策单调性需要使用二分队列,复杂度 \(O(n^2logn)\) 。斜优的话 \(O(n^2)\) ,不过这里不是复杂度瓶颈,随便写什么都行。
前面的复杂度 \(O(pn^2logn)\) ,然后考虑怎么合并。
暴力合并是 \(O(n^5)\) 的,不能通过此题。
容易发现,对于每一个 \(i\) 并不是 \(j\) 越大花的时间越长,打表发现他是单谷的,合理猜测之后尝试证明。
\(f[i][j]=min(calc(i,k)+cost(j,k))\) \(calc(i,k)\) 表示 \(A\) 的贡献,可以分成 \(k-1,k,k+1\) 段。而 \(cost(j,k)\) 就是 \(B\) 分成 \(k\) 段的贡献,发现 \(calc(i,k)=min(cost(i,k-1),cost(i,k),cost(i,k+1))\) 。考虑对于固定一个 \(k\) , \(cost(j,k)\) 随着 \(j\) 的增大而递增,并且是一个下凸壳,也就是二阶导数非负,而 \(calc(i,k)\) 随着 \(k\) 的增加是单谷的,考虑这个实质就是在 \(calc(i,k)\) 上每一个点向右延伸出 \(cost(j,k)\) 的图像,再取 \(min\) 并把 \(k\) 轴替换为 \(j\) 轴,就可以通过画图或者感性理解证明是单谷的。

变成:
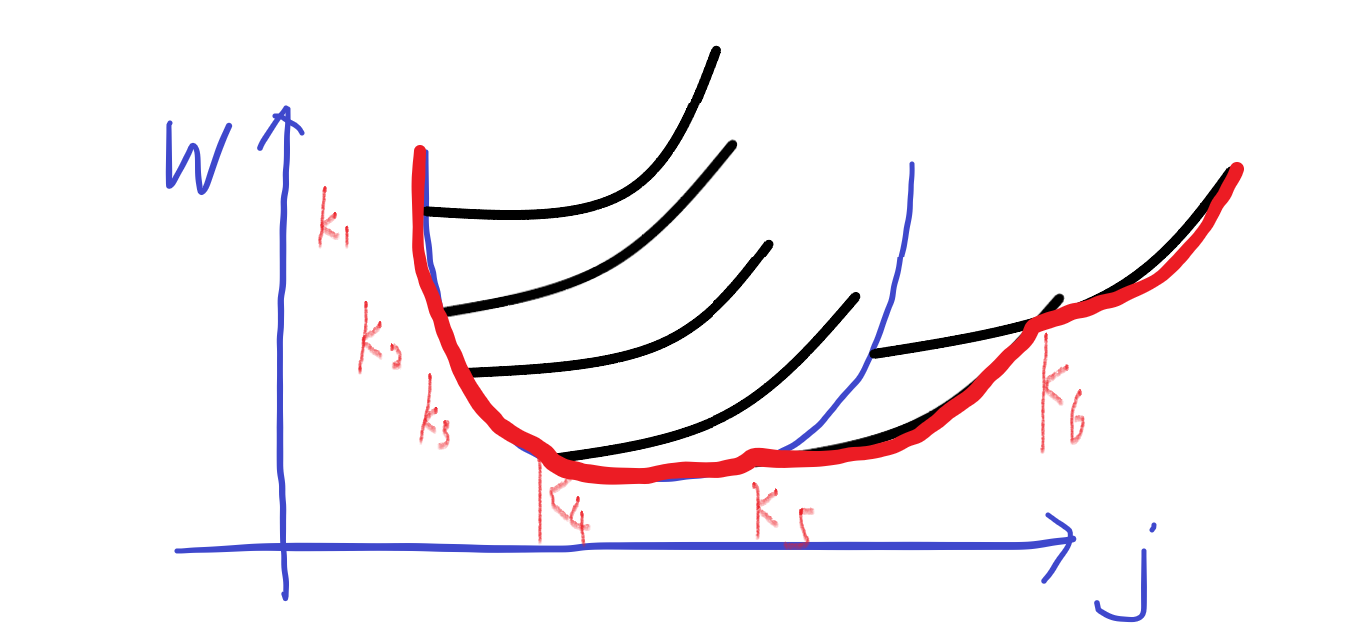
然后就可以二分答案, \(dp[i][j]\) 表示前 \(i\) 个选了 \(j\) 个A,可能B数量的区间,复杂度 \(O(n^3logW)\) ,可以通过。
附录:
一个函数的图像如果上凸,则一阶导数单调不减,即二阶导数>=0。
一个函数的图像如果下凸,则一阶导数单调不增,即二阶导数<=0。
T4:
很显然的一点是,最大值只会有一个,把最大值扣掉之后就可以分治去处理这个问题,想到点分治,因此证明 \(log2(n)+1\) 是答案的上界。
但是我们显然不能证明点分树的层数就是答案,提供一个hack:
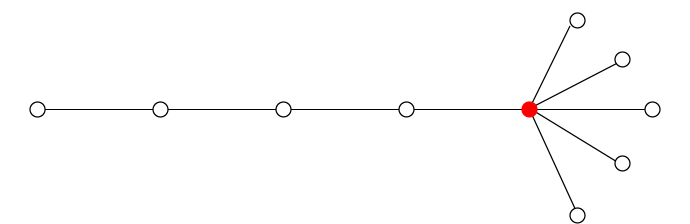
答案应该是3,而点分树层数是4。
不过有了这个性质我们就可以进行最为基础状压dp,复杂度 \(O(n^2)\) 或者带个 \(log\) 你都可以获得60分的好成绩。
比较厉害的是这题还有进一步的性质,性质为先递归字数,再贪心每次填自己可以填的最小的,最后每一位的最大值就是答案。
证明较为复杂:
记一个函数fk(S1,S2……Sk)。其中k表示参数的个数,Si描述一个子树的溢出集合,它可以是一个二进制数,形式是,aj是0或1,aj=1当且仅当标号j在溢出集合中。为了方便,它还是一个集合,如果运算法则对数适用,它就是一个数,否则就是一个集合。函数fk的返回值就是当一个节点有k个儿子树时,第i个子树的溢出集合是Si时,根节点的最小标号是多少。
再定义一个函数Fk(S1,S2……Sk),表示一个节点有k个儿子树,第i个子树的一处集合是Si,对这个节点标号fk(S1,S2……Sk),以这个节点为根的树的溢出集合。
不难看出,标号要与任意一个子树溢出集合中的任意一个标号不同,也要比任意一个在两个不同溢出集合中的标号要大,这样,就不难得出下面式子:
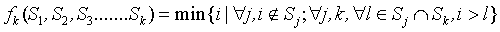
设函数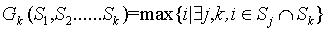 。
。
有下面结论:
①一个k个儿子树的溢出集合分别为S1,S2……Sk的树,它的根节点标号为fk(S1,S2……Sk)时,这棵树的溢出集合最小(这个“小”就可以把集合看成二进制数)。
②如果S’k>Sk,那么Fk(S1,S2……Sk -1,S’k)≥Fk(S1,S2……Sk)。
结论①的证明:令t=Gk(S1,S2……Sk),,显然,根节点的标号要大于t,在这个前提下,还要满足不属于T,如果根节点的标号是t1,那么,把t1加到T中,并且把小于t1的标号都从T中删除,这时的T就是这个树的溢出集合,不难发现,t1越小,这个集合就越小,而t1的最小值就是fk(S1,S2……Sk),所以结论①成立。
结论②的证明:令t=Gk(S1,S2……Sk -1),。由于Sk中小于等于t的元素是没有意义的。当t>0时,只需要把每一个S,S’,T都除以2t取整,这样不会影响他们的大小关系,所以下面值需要证明t=0的情况。更进一步,只需要证明S’k 比Sk大1的情况,即S’k=Sk+1。设t1表示最小的不在Sk中的标号,有3种情况:
情况1:Sk与T的交集中有元素大于t1,这时,②两边相等;
情况2:不满足情况1且t1∈T,这时S’k与T有交集{t1},这时不难发现fk(S1,S2……S’k)= fk(S1,S2……Sk)>t1,所以②两边仍然相等。
情况3:不满足情况1,2,即Sk与T交集中所有的元素都小于t1,并且t1既不在Sk中,也不在T 中。这时,Fk(S1,S2……Sk)=(Sk∪T)+1,即Sk与T的并去掉1..t1-1中的元素在加上元素t1,而这些元素都在S’k∪T中,而②左边相当于(S’k∪T)+1。Fk(S1,S2……Sk)=(S’k∪T)+1>S’k∪T≥Fk(S1,S2……Sk)。这种情况左边大于右边。
所以结论②也证明了。
综合看结论①与结论②。如果我们要使整棵树的溢出集合尽量的小(这样一定能够保证最大顶点标号最小),就要使每一个儿子树的一处集合尽量的小(结论②),然后在这个前提下,使得根节点标号尽量的小(结论①)。这个就证明了上面贪心法的正确性。
相比这个结论的复杂代码就显得极为simple,你想写 \(O(nlogn)\) 或者 \(O(n)\) 都是给过的。而优化一个 \(log\) 也不需要什么高深的技巧,只要位运算就行了