\({\color{Red}{欢迎到学科网下载资料学习 }}\)
[ 【基础过关系列】高一数学同步精品讲义与分层练习(人教A版2019）]
(https://www.zxxk.com/docpack/2921718.html)
\({\color{Red}{ 跟贵哥学数学，so \quad easy！}}\)

必修第二册同步巩固，难度2颗星！

基础知识

平面

无限延展，无边界.
判断
一张纸是一个平面(×)；平面\(ABCD\)就是四边形\(ABCD\) (×)；两个平面可相交于一点 (×).
原因均是平面是无限延展的.
 

图形语言，文字语言，符号语言的转化

图形语言	文字语言	符号语言
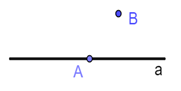	点\(A\)在直线\(a\)上，点\(B\)在直线\(a\)外	\(A \in a，B \notin a\)
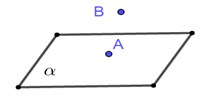	点\(A\)在平面\(\alpha\)内，点\(B\)在平面\(\alpha\)外	\(A \subset \alpha，B \nsubseteq \alpha\)
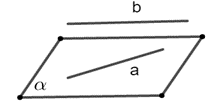	直线\(a\)在平面\(\alpha\)内，直线\(b\)在平面\(\alpha\)外	\(a \subset \alpha，b \nsubseteq \alpha\)
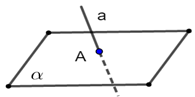	直线\(a\)与平面\(\alpha\)相交于点	\(a \cap \alpha=A\)
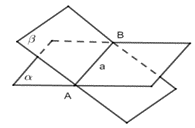	平面\(\alpha\)与平面\(\beta\)相交于直线\(a\)	\(\alpha \cap \beta=a\)

注 点用大写字母表示，直线用小写字母表示，平面用希腊字母表示.
 

三个基本事实与三个推论

(1) 基本事实1
不共线的三点确定一个平面.

解释
① 用途:用于确定平面.
② “确定”的意思是“有且只有”，过不共线三点的平面有且只有一个，故说确定一个平面.
③ 判断 三点确定一个平面 (×)；原因是三点未必共线.
 

(2) 基本事实2
如果一条直线上有两点在一个平面内，那么直线在平面内.

符合表示：\(A∈m\)，\(B\in m\)，且\(A\in \alpha\) \(，B\in \alpha ⇒m \subset \alpha\) .
用途:常用于证明直线在平面内.
 

(3) 基本事实3
如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线.
符合表示：\(A\in \alpha\) ，且\(A\in β⇒\alpha ∩β=a\)，且\(A\in a\).
用途:常用于证明线在面内，证明点在线上.

推论1:直线与直线外的一点确定一个平面.
推论2:两条相交直线确定一个平面.
推论3:两条平行直线确定一个平面.

 

基本方法

【题型1】 三种语言的转换

【典题1】 (1)说明语句“\(l \subset \alpha\)，\(m\cap \alpha =A\)，\(A\notin l\)”表示的点、线、面的位置关系，并画出图形；
(2)用符号语言表示下图所表示的点、线、面的位置关系．

解析 (1)直线\(l\)在平面\(\alpha\)内，直线\(m\)与平面\(\alpha\)相交于点\(A\)，且点\(A\)不在直线\(l\)上，图形如图所示．

(2)图示的点、线、面的位置关系可用符号语言表示为\(\alpha \cap β=l\)，\(m \subset \alpha\)，\(n \subset β\)，\(l\cap n=P\)，\(m∥l\)．
 

【巩固练习】

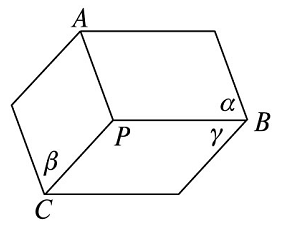
1.如图所示的点、线、面的位置关系用符号语言表示为\(\underline{\quad \quad}\)．

 

2.用符号语言表示“三个平面\(\alpha\)，\(\beta\)，\(\gamma\)相交于一点\(P\)，且平面\(\alpha\)与平面\(\beta\)交于\(PA\)，平面\(\alpha\)与平面\(\gamma\)交于\(PB\)，平面\(\beta\)与平面\(\gamma\)交于\(PC\)”，并画出图形．
 
 

参考答案

1. 答案 \(\alpha \cap β=l\)，\(m\cap \alpha =A\)，\(m\cap β=B\)，\(A\notin l\)，\(B\notin l\)
2. 答案 \(\alpha \cap \beta =PA\)，\(\alpha \cap \gamma=PB\)，\(\beta \cap \gamma=PC\)，\(PA\cap PB\cap PC=P\)．图形如图所示．
   

【题型2】 共点、共线、共面问题

【典题1】 如图所示，正方体\(ABCD—A_1 B_1 C_1 D_1\)中，\(E\)、\(F\)分别是\(AB\)和\(AA_1\)的中点．求证
  (1)\(E\)、\(C\)、\(D_1\) 、\(F\)四点共面；\(\qquad \qquad\) (2)\(CE\)、\(D_1 F\)、\(DA\)三线共点．

证明
(1)连接\(EF\)，\(CD_1\)，\(A_1 B\).

\(\because E\)、\(F\)分别是\(AB\)和\(AA_1\)的中点，\(\therefore EF∥BA_1\).
又\(A_1 B∥D_1 C\)，\(\therefore EF∥CD_1\)，\(\therefore E\)、\(C\)、\(D_1\) 、\(F\)四点共面．
(2)\(\because EF∥CD_1\)，\(EF<CD_1\)，\(\therefore CE\)与\(D_1 F\)必相交，设交点为\(P\)，
则由\(P\in CE\)，\(CE \subset\)平面\(ABCD\)，得\(P\in\)平面\(ABCD\).
同理\(P\in\)平面\(ADD_1 A_1\).
又平面\(ABCD\cap\)平面\(ADD_1 A_1=DA\)，
\(\therefore P\in\)直线\(DA\)，
\(\therefore CE\)、\(D_1 F\)、\(DA\)三线共点．
 

【典题2】 如图，在四面体\(ABCD\)中，\(E\)，\(G\)分别为\(BC\)，\(AB\)上的点，\(H\)，\(F\)分别为\(AD\)，\(CD\)上的点，\(GH\)与\(EF\)交于点\(O\)．求证：\(B\)，\(D\)，\(O\)在同一条直线上．

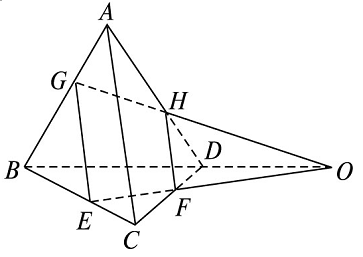
证明 \(\because GH\cap EF=O\)，\(\therefore O\in GH\)，\(O\in EF\)．
又\(GH \subset\) 平面\(ABD\)，\(EF \subset\)平面\(BCD\)，
\(\therefore O\in\)平面\(ABD\)，\(O\in\) 平面\(BCD\)．
\(\therefore\)点\(O\)在平面\(ABD\)与平面\(BCD\)的交线上．
又\(\because\)平面\(ABD\cap\) 平面\(BCD=BD\)，\(\therefore O\in BD\)．
\(\therefore B\)，\(D\)，\(O\)在同一条直线上．
 

【巩固练习】

1.下列说法错误的是(　　)
 A．空间中的三点确定一个平面 \(\qquad \qquad \qquad \qquad\) B．直线和直线外一点确定一个平面
 C．两条相交直线确定一个平面 \(\qquad \qquad \qquad \qquad\) D．两条平行直线确定一个平面
 

2.在长方体\(ABCD-A_1 B_1 C_1 D_1\)中，直线\(A_1 C\)与平面\(AB_1 D_1\)的交点为\(M\)，\(O\)为线段\(B_1 D_1\)的中点，则下列结论错误的是(　　)
 A．\(A\)，\(M\)，\(O\)三点共线 \(\qquad \qquad \qquad \qquad \qquad\) B．\(M\)，\(O\)，\(A_1\)，\(A\)四点共面
 C．\(B\)，\(B_1\)，\(O\)，\(M\)四点共面 \(\qquad \qquad \qquad \qquad\) D．\(A\)，\(O\)，\(C\)，\(M\)四点共面
 

3.已知直线\(a∥b\)，直线\(l\)与\(a\)，\(b\)都相交．求证：直线\(a\)，\(b\)，\(l\)共面．
 
 

4.在正方体\(ABCD—A_1 B_1 C_1 D_1\)中，对角线\(A_1 C\)与平面\(BDC_1\)交于点\(O\)，\(AC\)，\(BD\)交于点\(M\)，求证 点\(C_1\)，\(O\)，\(M\)共线．
 
 

5.如图，已知 \(E\)、\(F\)、\(G\)、\(H\)分别是正方体\(ABCD—A_1 B_1 C_1 D_1\)的棱\(AB\)、\(BC\)、\(CC_1\) 、\(C_1 D_1\)的中点，证明\(FE\)、\(HG\)、\(DC\)三线共点．

 
 
 

参考答案

1. 答案 \(A\)
   解析 对于\(A\)，由公理\(2\)可知：过不在同一直线上的三点有且只有一个平面，故\(A\)错误；
   对于\(C\)，由公理\(2\)的推论可知：经过两条相交直线有且只有一个平面，故选项\(C\)正确；
   对于\(B\)，由公理\(2\)的推论可知：经过一条直线和这条直线外一点有且只有一个平面，故选项\(B\)正确；
   对于\(D\)，由公理\(2\)的推论可知：经过两条平行直线有且只有一个平面，故选项\(D\)正确，
   故选：\(A\)．

2. 答案 \(C\)
   解析 连接\(A_1 C_1\)，\(AC\)，则\(A_1 C_1∥AC\)，\(A_1\)，\(C_1\)，\(C\)，\(A\)四点共面，
   所以\(A_1 C \subset\)平面\(ACC_1 A_1\)，因为\(M\in A_1 C\)，所以\(M\in\)平面\(ACC_1 A_1\)，
   又\(M\in\)平面\(AB_1 D_1\)，所以\(M\)在平面\(ACC_1 A_1\)与平面\(AB_1 D_1\)的交线上，
   同理\(O\)在平面\(ACC_1 A_1\)与平面\(AB_1 D_1\)的交线上，
   所以\(A\)，\(M\)，\(O\)三点共线．
   选项\(A\)、\(B\)、\(D\)均正确，选项\(C\)错误．
   故选：\(C\)．
   

3. 证明 \(\because a∥b\)，
   \(\therefore\)直线\(a\)，\(b\)确定一个平面，记为\(\alpha\)，如图．
   
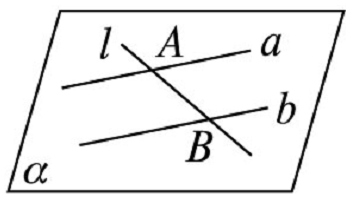
   设\(a\cap l=A\)，\(b\cap l=B\)，
   则\(A\in a\)，\(B\in b\)，\(\therefore A\in \alpha\) ，\(B\in \alpha\) ．
   \(\therefore l \subset \alpha\)．\(\therefore\)直线\(a\)，\(b\)，\(l\)共面．

4. 证明 如图所示，\(\because A_1 A∥C_1 C\)，
   \(\therefore A_1 A\)，\(C_1 C\)确定平面\(A_1 C\).
   \(\because A_1 C \subset\)平面\(A_1 C\)，\(O\in A_1 C\)，
   \(\therefore O\in\)平面\(A_1 C\)，而\(O=\)平面\(BDC_1\cap\) 线\(A_1 C\)，
   \(\therefore O\in\)平面\(BDC_1\)，
   \(\therefore O\)在平面\(BDC_1\)与平面\(A_1 C\)的交线上．
   \(\because AC\cap BD=M\)，\(\therefore M\in\) 平面\(BDC_1\)且\(M\in\)平面\(A_1 C\)，
   \(\therefore\)平面\(BDC_1\cap\)平面\(A_1 C=C_1 M\)，
   \(\therefore O\in C_1 M\)，即\(C_1\)，\(O\)，\(M\)三点共线．
   

5. 证明 连结\(C_1 B\)，\(HE\)，\(FG\)，由题意知\(HC_1//EB\)， \(HC_1=EB\)，
   \(\therefore\)四边形 \(HC_1 BE\)是平行四边形．\(\therefore HE∥C_1 B\).
   又\(C_1 G=GC=CF=BF\)，故\(GF=\dfrac{1}{2} C_1 B\)，\(GF//C_1 B\)
   \(\therefore GF∥HE\)，且\(GF≠HE\)，\(\therefore HG\)与\(EF\)相交．
   设交点为\(K\)，则\(K\in HG\)，\(HG \subset\)平面\(D_1 C_1 CD\)，
   \(\therefore K\in\)平面\(D_1 C_1 CD\).
   \(\because K\in EF\)，\(EF \subset\)平面\(ABCD\)，\(\therefore K\in\) 平面\(ABCD\).
   \(\because\)平面\(D_1 C_1 CD\cap\)平面\(ABCD=DC\)，
   \(\therefore K\in DC\)，\(\therefore FE\)、\(HG\)、\(DC\)三线共点．
   
    

【题型3】截面问题

【典题1】 如图，已知\(P\)、\(Q\)、\(R\)分别是正方体\(ABCD-A_1 B_1 C_1 D_1\)的棱\(AB\)、\(BC\)和\(C_1 D_1\)的中点，由点\(P\)、\(Q\)、\(R\)确定的平面\(\beta\)截该正方体所得截面为(　　)

 A．三角形 \(\qquad \qquad \qquad \qquad\) B．四边形 \(\qquad \qquad \qquad \qquad\)C．五边形 \(\qquad \qquad \qquad \qquad\) D．六边形
解析 作\(RT\)平行\(PQ\)，交\(A_1 D_1\)于点\(T\)，
取\(AA_1\)的中点\(M\)，\(CC_1\)的\(S\)，连接\(PM\)、\(TM\)、\(RS\)、\(QS\)，
可得过\(PQR\)的截面为六边形\(PQSRTM\)．
故选：\(D\)．

 

【典题2】 棱长为\(2\)的正方体\(ABCD-A_1 B_1 C_1 D_1\)中，\(E\)，\(F\)分别是棱\(C_1 D_1\)和\(C_1 B_1\)的中点，则经过点\(B\)，\(E\)，\(F\)的平面截正方体所得的封闭图形的面积为(　　)
 A．\(\dfrac{9}{2}\) \(\qquad \qquad \qquad \qquad\) B．\(3 \sqrt{10}\) \(\qquad \qquad \qquad \qquad\)C．\(\dfrac{3}{2}\) \(\qquad \qquad \qquad \qquad\) D． \(\sqrt{10}\)
解析 经过点\(B\)，\(E\)，\(F\)的平面截正方体所得的封闭图形为梯形\(EFBD\)，
可得 \(D B=2 \sqrt{2}\)， \(E F=\sqrt{2}\)， \(D E=B F=\sqrt{5}\)，
则梯形的高 \(h=\sqrt{(\sqrt{5})^2-\left(\dfrac{\sqrt{2}}{2}\right)^2}=\sqrt{\dfrac{9}{2}}\)，
则梯形\(EFBD\)的面积为 \(S=\dfrac{1}{2}(2 \sqrt{2}+\sqrt{2}) \times \dfrac{3}{\sqrt{2}}=\dfrac{9}{2}\)．
故选：\(A\)．

 

【巩固练习】

1.用一个平面截正方体，截面可能出现的形状是(　　)
①等边三角形 \(\qquad \qquad\) ②直角梯形\(\qquad \qquad\) ③菱形\(\qquad \qquad\) ④五边形
 A．①②③ \(\qquad \qquad \qquad \qquad\) B．①②④ \(\qquad \qquad \qquad \qquad\)C．①③④ \(\qquad \qquad \qquad \qquad\) D．②③④
 

2.正方体\(ABCD﹣A'B'C'D'\)的棱长为\(2\)，\(E\)为棱\(BB'\)的中点，用过点\(A\)，\(E\)，\(C'\)的平面截取该正方体，则截面的面积为(　　)

 A． \(2 \sqrt{6}\) \(\qquad \qquad \qquad \qquad\) B． \(2 \sqrt{5}\) \(\qquad \qquad \qquad \qquad\)C．\(5\) \(\qquad \qquad \qquad \qquad\) D． \(4 \sqrt{2}\)
 

3.如图，在棱长为\(2\)的正方体\(ABCD-A_1 B_1 C_1 D_1\)中，\(E\)是棱\(CC_1\)的中点，则过三点\(A\)，\(D_1\)，\(E\)的截面面积等于(　　)

 A． \(3 \sqrt{2}\) \(\qquad \qquad \qquad \qquad\) B． \(\dfrac{3 \sqrt{10}}{2}\) \(\qquad \qquad \qquad \qquad\)C． \(\dfrac{9}{2}\) \(\qquad \qquad \qquad \qquad\) D．\(3\)
 

参考答案

1. 答案\(C\)
   解析 用任意一个平面去截一个正方体，得到的截面如图：
   
   故可以是①等边三角形；③菱形；④五边形．
   故选：\(C\)．

2. 答案\(A\)
   解析 取\(DD'\)中点\(F\)，连结\(AF\)、\(C'F\)，
   则菱形\(AEC'F\)就是过点\(A\)，\(E\)，\(C'\)的平面截正方体所得截面，
   \(E F=B D=2 \sqrt{2}\)， \(A C^{\prime}=2 \sqrt{3}\)，
   \(\therefore\)用过点\(A\)，\(E\)，\(C'\)的平面截该正方体，则截面积为：
   \(S_{\text {菱形AEC } A C^{\prime} F}=\dfrac{1}{2} \times E F \times A C^{\prime}=\dfrac{1}{2} \times 2 \sqrt{2} \times 2 \sqrt{3}=2 \sqrt{6}\)．
   故选：\(A\)．
   

3. 答案 \(C\)
   解析 取\(BC\)的中点\(F\)，连接\(EF\)，\(AF\)，则\(EF∥AD_1\)，所以平面\(AD_1 EF\)为所求截面，
   \(EF=\sqrt{2}\)，\(AD_1=2\sqrt{2}\)， \(A F=\sqrt{2^2+1^2}=\sqrt{5}\)，
   所以梯形的高为： \(\sqrt{(\sqrt{5})^2-\left(\dfrac{\sqrt{2}}{2}\right)^2}=\dfrac{3 \sqrt{2}}{2}\)，
   过三点\(A\)，\(D_1\)，\(E\)的截面面积： \(\dfrac{2 \sqrt{2}+\sqrt{2}}{2} \times \dfrac{3 \sqrt{2}}{2}=\dfrac{9}{2}\)．
   故选：\(C\)．
   
    

分层练习

【A组---基础题】

1.下列图形中不一定是平面图形的是 (　　)
 A．三角形 \(\qquad \qquad \qquad\) B．四边相等的四边形 \(\qquad \qquad \qquad\) C．梯形 \(\qquad \qquad \qquad\)D．平行四边形
 

2.设\(P\)表示一个点，\(a\)，\(b\)表示两条直线，\(\alpha\)，\(\beta\)表示两个平面，给出下列四个命题，其中正确的命题是 (　　)
①\(P\in a\)，\(P\in \alpha ⇒a \subset \alpha\) 　
②\(a\cap b=P\)，\(b \subset \beta ⇒a \subset \beta\)　
③\(a∥b\)，\(a \subset \alpha\) ，\(P\in b\)，\(P\in \alpha ⇒b \subset \alpha\) 　
④\(\alpha \cap \beta =b\)，\(P\in \alpha\) ，\(P\in \beta ⇒P\in b\)
 A．①② \(\qquad \qquad \qquad \qquad\) B．②③ \(\qquad \qquad \qquad \qquad\) C．①④ \(\qquad \qquad \qquad \qquad\) D．③④
 

3.下列命题正确的是 (　　)
 Ａ．经过三点确定一个平面 \(\qquad \qquad \qquad \qquad\) Ｂ．经过一条直线和一个点确定一个平面
 Ｃ．四边形确定一个平面 \(\qquad \qquad \qquad \qquad\) Ｄ．两两相交且不共点的三条直线确定一个平面
 

4.过棱长为\(1\)的正方体的一条体对角线作截面，则截得正方体的截面面积的最小值 (　　)
 A．\(1\) \(\qquad \qquad \qquad \qquad\) B．\(\sqrt{2}\) \(\qquad \qquad \qquad \qquad\) C． \(\dfrac{\sqrt{3}}{2}\) \(\qquad \qquad \qquad \qquad\) D． \(\dfrac{\sqrt{6}}{2}\)
 

5.(多选)用一个平面去截一个几何体，所得截面的形状是正方形，则原来的几何体可能是(　　)
 A．长方体 \(\qquad \qquad \qquad \qquad\) B．圆台 \(\qquad \qquad \qquad \qquad\)C．四棱台 \(\qquad \qquad \qquad \qquad\) D．正四面体
 

6.如图，棱长为\(1\)的正方体\(ABCD-A_1 B_1 C_1 D_1\)中，\(P\)为\(A_1 D_1\)中点，则过P、\(A\)、\(C\)三点的截面面积为\(\underline{\quad \quad}\)．

 

7.已知三个平面\(\alpha\) ，\(\beta\)，\(\gamma\)两两相交于三 条直线，即\(\alpha \cap \beta =c\)，\(\beta \cap \gamma=a\)，\(\gamma\cap \alpha =b\)，若直线\(a\)和\(b\)不平行，
求证：\(a\)，\(b\)，\(c\)三条直线必过同一点．
 
 
 

8.在空间四边形\(ABCD\)中，\(H\)，\(G\)分别是\(AD\)，\(CD\)的中点，\(E\)，\(F\)分别边\(AB\)，\(BC\)上的点，且\(\dfrac{C F}{F B}=\dfrac{A E}{E B}=\dfrac{1}{3}\)．求证
①点\(E\)，\(F\)，\(G\)，\(H\)四点共面；\(\qquad \qquad\)②直线\(EH\)，\(BD\)，\(FG\)相交于一点．

 
 
 

参考答案

1. 答案 \(B\)
   解析 \(A\)、由不共线的三点确定一个平面和图形知，三角形是平面图形，故\(A\)不对；
   \(B\)、当空间四边形的四边相等时，是空间几何体而不是平面图形，故\(B\)对；
   \(C\)、因梯形的一组对边相互平行，则由两条平行线确定一个平面知，梯形是平面图形，故\(C\)不对；
   \(D\)、因平行四边形的对边相互平行，则由两条平行线确定一个平面知，平行四边形是平面图形，故\(D\)不对；
   故选\(B\)．

2. 答案 \(D\)
   解析 当\(a\cap \alpha =P\)时，\(P\in a\)，\(P\in \alpha\)，但\(a⊄\alpha\)，①错；\(a\cap \beta =P\)时，②错；
   如图，\(\because a∥b\)，\(P\in b\)，\(\therefore P\notin a\)，\(\therefore\)由直线\(a\)与点\(P\)确定唯一平面\(\alpha\)，
   
   又\(a∥b\)，由\(a\)与\(b\)确定唯一平面\(\beta\) ，但\(\beta\)经过直线\(a\)与点\(P\)，
   \(\therefore \beta\)与\(\alpha\)重合，\(\therefore b \subset \alpha\)，故③正确；
   两个平面的公共点必在其交线上，故④正确．

3. 答案 \(D\)
   解析 对于\(A\)，若三点共线时就错了；对于\(B\)，若点在直线上，是不能确定一个平面的；
   对于\(C\)，空间四边形就不属于平面图形，注意四边形在立体几何里分为平面四边形和空间四边形了.

4. 答案 \(D\)
   解析 取\(AA_1\)的中点\(E\)，\(CC_1\)的中点\(F\)，
   连接\(BE\)、\(ED_1\)、\(D_1 F\)、\(FB\)，如图所示；
   四边形\(BED_1 F\)为过棱长为\(1\)的正方体的一条体对角线\(BD_1\)所作截面的面积最小的截面，
   且四边形\(BED_1 F\)是菱形，其截面面积为\(\dfrac{1}{2} \cdot B D_1 \cdot E F=\dfrac{1}{2} \times \sqrt{3} \times \sqrt{2}=\dfrac{\sqrt{6}}{2}\)．
   故选 \(D\)．
   

5. 答案 \(ACD\)
   解析 对于\(A\)：若长方体的底面为正方形，则用平行于底面的平面去截几何体，所得截面的形状是正方形，故\(A\)正确；
   对于\(B\)：圆台的截面均不可能是正方形，故\(B\)错误；
   对于\(C\)：若四棱台的底面是正方形，则用平行于底面的平面去截几何体，所得截面的形状是正方形，故\(C\)正确；
   对于\(D\)：如图所示正四面体\(S﹣ABC\)，将其放到正方体中，
   取\(SB\)的中点\(E\)，\(SC\)的中点\(D\)，取\(AB\)的中点\(F\)，\(AC\)的中点\(DG\)，
   依次连接\(EF\)、\(FG\)、\(GD\)、\(DE\)，由正方体的性质可知截面\(DEFG\)为正方形，故\(D\)正确；
   
   故选：\(ACD\)．

6. 答案 \(\dfrac{9}{8}\)
   解析 作\(PQ∥AC\)交\(D_1 C_1\)于\(Q\)，因为\(P\)为中点，所以过\(P\)、\(A\)、\(C\)三点的截面为四边形\(PACQ\)，
   所以 \(P Q=\dfrac{1}{2} A C=\dfrac{\sqrt{2}}{2}\)，\(AC=\sqrt{2}\)，可得四边形\(PACQ\)为梯形，
   过\(PM⊥A_1 C_1\)交于\(M\)，过\(M\)作\(MN⊥AC\)交于\(N\)，可得 \(P M=\dfrac{\sqrt{2}}{4}\)，
   在正方体中，\(A_1 C_1∥AC\)，所以\(MN⊥AC\)，而\(PM\cap MN=M\)，
   所以\(AC⊥\)面\(PMN\)，可得\(AC⊥PN\)，
   即梯形\(APQC\)的高为\(PN\)，可得\(MN⊥\)面\(A_1 C_1\)，可得\(MN⊥PM\)， \(PN=\sqrt{\mathrm{PM}^2+\mathrm{MN}^2}=\sqrt{\dfrac{2}{16}+1}=\sqrt{\dfrac{9}{8}}=\dfrac{3 \sqrt{2}}{4}\)，
   所以$S_{\text {梯形 } P A C Q}=\dfrac{1}{2}(P Q+A C) \cdot P N=\dfrac{1}{2}\left(\dfrac{\sqrt{2}}{2}+\sqrt{2}\right) \cdot \dfrac{3 \sqrt{2}}{4}=\dfrac{9}{8} $，
   故答案为： \(\dfrac{9}{8}\)．
   

7. 证明 \(\because \alpha \cap \gamma=b\)，\(\beta \cap \gamma=a\)，
   \(\therefore a \subset \gamma\)，\(b \subset \gamma\)．
   又由于直线\(a\)和\(b\)不平行，
   \(\therefore a\)，\(b\)必相交．
   设\(a\cap b=P\)，如图，则\(P\in a\)，\(P\in b\)．
   
   \(\because a \subset \beta\) ，\(b \subset \alpha\)，\(\therefore P\in \beta\)，\(P\in \alpha\) ．
   又\(\alpha \cap \beta =c\)，
   \(\therefore P\in c\)，即交线\(c\)经过点\(P\)．
   \(\therefore a\)，\(b\)，\(c\)三条直线相交于同一点.

8. 证明 ①如图所示，
   空间四边形\(ABCD\)中，\(H\)，\(G\)分别是\(AD\)，\(CD\)的中点，\(\therefore HG∥AC\)；
   又\(\dfrac{C F}{F B}=\dfrac{A E}{E B}=\dfrac{1}{3}\)，\(\therefore EF∥AC\)，
   \(\therefore EF∥HG\)，
   \(\therefore E\)、\(F\)，\(G\)，\(H\)四点共面；
   ②设\(EH\)与\(FG\)交于点\(P\)，
   \(\because EH \subset\)平面\(ABD\)，\(\therefore P\)在平面\(ABD\)内，
   同理\(P\)在平面\(BCD\)内，
   且平面\(ABD\cap\)平面\(BCD=BD\)，
   \(\therefore\)点\(P\)在直线\(BD\)上，
   \(\therefore\)直线\(EH\)，\(BD\)，\(FG\)相交于一点．
   
    

【B组---提高题】

1.三个平面把空间最少分为\(\underline{\quad \quad}\)部分，最多可分为\(\underline{\quad \quad}\)部分．
 

2.在正方体\(ABCD-A_1 B_1 C_1 D_1\)中，\(E\)，\(F\)分别为棱\(AA_1\)，\(CC_1\)的中点，则在空间中与三条直线\(A_1 D_1\)，\(EF\)，\(CD\)都相交的直线有 \(\underline{\quad \quad}\)条．
 

3.如图，棱长为\(2\)的正方体\(ABCD—A_1 B_1 C_1 D_1\)中，点\(E\)、\(F\)分别为\(AB\)、\(BC\)的中点，则平面\(D_1 EF\)截该正方体所得截面的面积为 \(\underline{\quad \quad}\)．

 
 

参考答案

1. 答案 \(4\) ，\(8\)
2. 答案 无数
   解析 　方法一　在\(EF\)上任意取一点\(M\)，直线\(A_1 D_1\)与\(M\)确定一个平面，这个平面与\(CD\)有且仅有\(1\)个交点\(N\)，当\(M\)取不同的位置时就确定不同的平面，从而与\(CD\)有不同的交点\(N\)，而直线\(MN\)与这\(3\)条异面直线都有交点．如图所示．
   
   方法二　在\(A_1 D_1\)上任取一点\(P\)，过点\(P\)与直线\(EF\)作一个平面\(\alpha\)，因\(CD\)与平面\(\alpha\)不平行，所以它们相交，设它们交于点\(Q\)，连接\(PQ\)，则\(PQ\)与\(EF\)必然相交，即\(PQ\)为所求直线．由点P的任意性，知有无数条直线与三条直线\(A_1 D_1\)，\(EF\)，\(CD\)都相交．
3. 答案 \(\dfrac{7 \sqrt{17}}{6}\)
   解析 如图，延长\(EF\)，\(FE\)，分别交\(DC\)，\(DA\)的延长线于点\(H\)，\(G\)，
   连结\(D_1 G\)，\(D_1 H\)，分别交\(AA_1\)，\(CC_1\)于点\(I\)，\(J\)，
   则五边形\(D_1 IEFJ\)为所求截面．
   \(\because\)平面\(DC_1∥\)平面\(AB_1\)，
   \(\therefore\)平面\(D_1 GH\)与之交线\(IE∥D_1 J\)，
   \(\therefore △GIE∽△GD_1 H\)，
   \(\therefore S_{\triangle G I E}: S_{\triangle G D_1 H}=G E^2: G H^2\)，
   \(\because GE GH=AE DH=1: 3\)，
   \(\therefore S_{\triangle G I E}: S_{\triangle G D_1 H}=1: 9\)，
   同理， \(S_{\triangle H J F}: S_{\triangle D_1 G H}=1: 9\)，
   \(\therefore S_{D_1 I E F J}=\dfrac{7}{9} S_{\triangle D_1 G H}\)， \(\therefore S_{\triangle D_1 G H}=\dfrac{3 \sqrt{17}}{2}\)，
   \(\therefore S_{D_1 I E F J}=\dfrac{7}{9} \times \dfrac{3 \sqrt{17}}{2}=\dfrac{7 \sqrt{17}}{6}\)．
   
    

【C组---拓展题】

1.如图，正方体\(ABCD—A_1 B_1 C_1 D_1\)棱长为\(1\)，\(P\)为\(BC\)中点，\(Q\)为线段\(CC_1\)上动点，过点\(A\)，\(P\)，\(Q\)的平面截该正方体所得截面记为\(S\)．当\(CQ=\dfrac{1}{2}\)时，\(S\)的面积为\(\underline{\quad \quad}\)；若\(S\)为五边形，则此时\(CQ\)取值范围\(\underline{\quad \quad}\)．

 
 

参考答案

1. 答案 \(\dfrac{9}{8}\)； \(\left(\dfrac{1}{2}， 1\right)\)
   解析 如图
   
   当\(CQ=\dfrac{1}{2}\)时，即\(Q\)为\(CC_1\)中点，此时可得\(PQ∥AD_1\)， \(A P=Q D_1=\dfrac{\sqrt{5}}{2}\)，
   故可得截面\(APQD_1\)为等腰梯形，
   \(\therefore S=\dfrac{1}{2}\left(\sqrt{2}+\dfrac{\sqrt{2}}{2}\right) \cdot \dfrac{3 \sqrt{2}}{4}=\dfrac{9}{8}\)；
   当\(C Q=\dfrac{3}{4}\)时，如下图，
   
   延长\(DD_1\)至\(N\)，使\(D_1 N=\dfrac{1}{2}\)，连结\(AN\)交\(A_1 D_1\)于\(S\)，
   连结\(QN\)交\(C_1 D_1\)于\(R\)，连结\(SR\)，则\(AN∥PQ\)，
   由\(△NRD_1∽△QRC_1\)，可得\(C_1 R:D_1 R=C_1 Q: D_1 N=1:2\)．
   \(\therefore C_1 R=\dfrac{1}{3}\)， \(R D_1=\dfrac{2}{3}\)，
   
   \(\therefore\)当\(\dfrac{1}{2} <CQ <1\)时，此时的截面形状是上图所示的\(APQRS\)，为五边形．