\({\color{Red}{欢迎到学科网下载资料学习 }}\)
[ 【基础过关系列】高一数学同步精品讲义与分层练习(人教A版2019）]
(https://www.zxxk.com/docpack/2921718.html)
\({\color{Red}{ 跟贵哥学数学，so \quad easy！}}\)

必修第二册同步巩固，难度2颗星！

基础知识

解三角形

一般地，三角形的三个角\(A\)，\(B\)，\(C\)和它们的对边\(a\)，\(b\)，\(c\)叫做三角形的元素。已知三角形的几个元素求其他元素的过程叫做解三角形.
 

余弦定理

1 内容
三角形中任何一边的平方，等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍.
即\(a^2=b^2+c^2-2bc\cos A\) ，\(b^2=a^2+c^2-2ac\cos B\)，\(c^2=a^2+b^2-2ab\cos C\).
2 变形
\(\cos A=\dfrac{b^2+c^2-a^2}{2 b c}\) ， \(\cos B=\dfrac{a^2+c^2-b^2}{2 a c}\) ， \(\cos C=\dfrac{a^2+b^2-c^2}{2 a b}\)
3 利用余弦定理可以解决下列两类三角形的问题
(1) 已知三边，可求三个角；(2) 已知两边和一角，求第三边和其他两个角.
 

正弦定理

1 内容
在一个三角形中，各边和它所对角的正弦的比相等，即
\(\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2 R\) (其中\(R\)是三角形外接圆半径)

2 变形
① \(\dfrac{a+b+c}{\sin A+\sin B+\sin C}=\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}\)
② 化边为角
\(a=2 R \sin A\) ，\(b=2R \sin ⁡B\) ，\(c=2R \sin ⁡C\)
\(a∶ b∶ c=\sin A∶ \sin B∶ \sin C\) ，
\(\dfrac{a}{b}=\dfrac{\sin A}{\sin B}\) ， \(\dfrac{b}{c}=\dfrac{\sin B}{\sin C}\) ，\(\dfrac{a}{c}=\dfrac{\sin A}{\sin C}\)
③ 化角为边
\(\sin A=\dfrac{a}{2 R}\)，\(\sin B=\dfrac{b}{2 R}\) ， \(\sin C=\dfrac{c}{2 R}\)
\(\dfrac{\sin A}{\sin B}=\dfrac{a}{b}\) ， \(\dfrac{\sin B}{\sin C}=\dfrac{b}{c}\) ， \(\dfrac{\sin A}{\sin C}=\dfrac{a}{c}\)
 

3 利用正弦定理可以解决下列两类三角形的问题
(1) 已知两个角及任意—边，求其他两边和另一角；
(2) 已知两边和其中—边的对角，求其他两个角及另一边.
 

面积公式

\(S_{\triangle A B C}=\dfrac{1}{2} a b \sin C=\dfrac{1}{2} b c \sin A=\dfrac{1}{2} ac\sin B\)

三角形解的个数问题

已知两边\(a\)、\(b\)和其中一边的对角\(A\)，不能确定三角形的形状，此时三角形解可能是无解、一解、两解，要分类讨论.

 

三角形类型的判断

\(\angle A=\dfrac{\pi}{2} \Rightarrow b^2+c^2=a^2\)；
\(\angle A>\dfrac{\pi}{2} \Rightarrow \cos A=\dfrac{b^2+c^2-a^2}{2 b c}<0 \Rightarrow b^2+c^2<a^2\)；
\(\angle A<\dfrac{\pi}{2} \Rightarrow \cos A=\dfrac{b^2+c^2-a^2}{2 b c}>0 \Rightarrow b^2+c^2>a^2\).
 

射影定理

\(a=c \cdot \cos B+b \cdot \cos C\) ，\(b=a \cdot \cos C+c \cdot \cos A\)，\(c=b \cdot \cos A+a \cdot \cos B\)

 

基本方法

经典例题

【典题1】如图，\(A\)，\(B\)是海平面上的两个点，相距\(800 m\)，在\(A\)点测得山顶\(C\)的仰角为\(45^{\circ}\)，\(∠BAD=120^{\circ}\)，又在\(B\)点测得\(∠ABD=45^{\circ}\)，其中\(D\)是点\(C\)到水平面的射影，求山高\(CD\).

解析 在\(△ABD\)中，\(∠BDA=180^{\circ}-45^{\circ}-120^{\circ}=15^{\circ}\).
由 \(\dfrac{A B}{\sin 15^{\circ}}=\dfrac{A D}{\sin 45^{\circ}}\)，得 \(A D=\dfrac{A B \cdot \sin 45^{\circ}}{\sin 15^{\circ}}=\dfrac{800 \times \dfrac{\sqrt{2}}{2}}{\dfrac{\sqrt{6}-\sqrt{2}}{4}}=800(\sqrt{3}+1)(m)\)．
\(\because CD⊥\)平面\(ABD\)，\(∠CAD=45^{\circ}\)，
\(\therefore C D=A D=800(\sqrt{3}+1)(m)\)．
\(\therefore\)山高\(CD\)为\(800(\sqrt{3}+1)m\).
 

【典题2】如图，一架飞机以\(600km/h\)的速度，沿方位角\(60^{\circ}\)的航向从\(A\)地出发向\(B\)地飞行，飞行了\(36min\)后到达\(E\)地，飞机由于天气原因按命令改飞\(C\)地，已知\(AD=600\sqrt{3} km\)，\(CD=1200km\) ， \(BC=500km\)，且\(∠ADC=30^{\circ}\)，\(∠BCD=113^{\circ}\)．问收到命令时飞机应该沿什么航向飞行，此时\(E\)地离\(C\)地的距离是多少？(参考数据： \(\tan 37^{\circ}=\dfrac{3}{4}\))

解析 连接\(AC\) ，\(CE\)，在\(△ACD\)中由余弦定理，得
\(A C^2=(600 \sqrt{3})^2+1200^2-2 \cdot 600 \sqrt{3} \cdot 1200 \cdot \dfrac{\sqrt{3}}{2}=360000\)，
\(\therefore AC=600\)，
则\(CD^2=AD^2+AC^2\)，
即\(△ACD\)是直角三角形，且\(∠ACD=60^{\circ}\)，
又\(∠BCD=113^{\circ}\)，则\(∠ACB=53^{\circ}\)，
\(\because \tan 37^{\circ}=\dfrac{3}{4}\)， \(\therefore \cos 53^{\circ}=\sin 37^{\circ}=\dfrac{3}{5}\)，
\(\therefore \cos \angle A C B=\dfrac{3}{5}\)
在\(△ABC\)中，由余弦定理得\(AB^2=600^2+500^2-2⋅600⋅500⋅\dfrac{3}{5}=500^2\)，
则\(AB=500\)，
又\(BC=500\)，则\(△ABC\)是等腰三角形，且\(∠BAC=53^{\circ}\)，
由已知有 \(A E=600 \cdot \dfrac{36}{60}=360\)，
在\(△ACE\)中，由余弦定理有 \(C E=\sqrt{360^2+600^2-2 \cdot 360 \cdot 600 \cdot \dfrac{3}{5}}=480\)，
又\(AC^2=AE^2+CE^2\)，则\(∠AEC=90^{\circ}\)．
由飞机出发时的方位角为 \(60^{\circ}\)，则飞机由\(E\)地改飞\(C\)地的方位角为\(90^{\circ}+60^{\circ}=150^{\circ}\)．
答：收到命令时飞机应该沿方位角\(150^{\circ}\)的航向飞行，\(E\)地离\(C\)地\(480km\)．
点拨
① 在实际问题时，理解仰角、俯角(它是在铅锤面上所成的角)，方位角(它是在水平面上所成的角)；
② 方位角是相对于某点而言，在确定方位角时要弄清楚时哪一个点的方位角；
③ 处理实际问题时要根据题意把实际问题的图形进行简化，并在图形上标出有关的角或边，明确最后实际要求的量可转化为三角形的什么量，再思考正弦定理或余弦定理解三角形.
 

【巩固练习】

1.如图，为了开凿隧道 ，要测量隧道上\(D\)，\(E\)间的距离，为此在山的一侧选取适当点\(C\)，测得\(CA=400 m\)，\(CB=600 m\)，\(∠ACB=60^{\circ}\)，又测得\(A\)，\(B\)两点到隧道口的距离\(AD=80 m\)，\(BE=40 m\)(\(A\)，\(D\)，\(E\)，\(B\)在一条直线上)，计算隧道\(DE\)的长．(精确到\(1 m\))

 
 
 

2.在某次军事演习中，红方为了准确分析战场形势，在两个相距 \(\dfrac{\sqrt{3}}{2} a\)的军事基地\(C\)和\(D\)测得蓝方两支精锐部队分别在\(A\)处和\(B\)处，且\(∠ADB=30^{\circ}\)，\(∠BDC=30^{\circ}\)，\(∠DCA=60^{\circ}\)，\(∠ACB=45^{\circ}\)，如图所示，求蓝方这两支精锐部队的距离．

3.为绘制海底地貌图，测量海底两点\(C\)，\(D\)间的距离，海底探测仪沿水平方向在\(A\)，\(B\)两点进行测量，\(A\)，\(B\)，\(C\)，\(D\)在同一个铅垂平面内．海底探测仪测得\(∠BAC=30^{\circ}\) ，\(∠DAC=45^{\circ}\)，\(∠ABD=45^{\circ}\) ，\(∠DBC=75^{\circ}\) ，同时测得\(AB=\sqrt{3}\)海里．
  (1)求的长度；
  (2)求\(C\)，\(D\)之间的距离．

 
 

4.如图所示，为美化环境，拟在四边形\(ABCD\)空地上修建两条道路\(EA\)和\(ED\)，将四边形分成三个区域，种植不同品种的花草，其中点\(E\)在边\(BC\)的三等分处(靠近\(B\)点)，\(BC=3\)百米，\(BC⊥CD\)，\(∠ABC=120^{\circ}\)，\(EA=\sqrt{21}\)百米，\(∠AED=60^{\circ}\) ．
  (1)求\(△ABE\)区域的面积；
  (2)为便于花草种植，现拟过\(C\)点铺设一条水管\(CH\)至道路\(ED\)上，求当水管\(CH\)最短时的长．

 
 

5.如图，海平面某区域内有\(A\)，\(B\)，\(C\)三座小岛，岛\(C\)在\(A\)的北偏东\(70^{\circ}\)方向，岛\(C\)在\(B\)的北偏东\(40^{\circ}\)方向，岛\(B\)在\(A\)的南偏东\(65^{\circ}\)方向，且\(A\)，\(B\)两岛间的距离为\(3\)海里．
  (1)求\(B\)，\(C\)两岛间的距离；
  (2)经测算海平面上一轮船\(D\)位于岛\(C\)的北偏西\(50^{\circ}\)方向，且与岛\(C\)相距\(3\sqrt{2}\)海里，求轮船在岛\(A\)的什么位置．(注：小岛与轮船视为一点)

 
 

参考答案

1. 答案 \(409 m\)
   解析在\(△ABC\)中，由余弦定理，得\(AB^2=AC^2+BC^2-2AC⋅BC\cos⁡∠ACB\)，
   \(\therefore A B^2=400^2+600^2-2 \times 400 \times 600 \cos 60^{\circ}=280000\).
   \(\therefore AB=200\sqrt{7}(m)\)．
   \(\therefore DE=AB-AD-BE=200\sqrt{7}-120≈409(m)\)．
   \(\therefore\)隧道\(DE\)的长约为\(409 m\).

2. 答案 \(\dfrac{\sqrt{6}}{4} a\)
   解析 \(\because ∠ADC=∠ADB+∠BDC=60^{\circ}\)，\(∠ACD=60^{\circ}\)，
   \(\therefore \angle D A C=60^{\circ}\)， \(\therefore A D=C D=\dfrac{\sqrt{3}}{2} a\)，
   在\(△BCD\)中，\(∠DBC=180^{\circ}-30^{\circ}-105^{\circ}=45^{\circ}\)，
   \(\because \dfrac{B D}{\sin \angle B C D}=\dfrac{C D}{\sin \angle D B C}\)，
   \(\therefore B D=C D \cdot \dfrac{\sin \angle B C D}{\sin \angle D B C}=\dfrac{\sqrt{3}}{2} a \cdot \dfrac{\dfrac{\sqrt{6}+\sqrt{2}}{4}}{\dfrac{\sqrt{2}}{2}}=\dfrac{3+\sqrt{3}}{4} a\).
   在\(△ADB\)中， \(\because A B^2=A D^2+B D^2-2 \cdot A D \cdot B D \cdot \cos \angle A D B\)
   \(=\dfrac{3}{4} a^2+\left(\dfrac{3+\sqrt{3}}{4} a\right)^2-2 \times \dfrac{\sqrt{3}}{2} a \dfrac{3+\sqrt{3}}{4} a \cdot \dfrac{3+\sqrt{3}}{4} a \cdot \dfrac{\sqrt{3}}{2}=\dfrac{3}{8} a^2\)，
   \(\therefore A B=\dfrac{\sqrt{6}}{4} a\).
   \(\therefore\)蓝方这两支精锐部队的距离为 \(\dfrac{\sqrt{6}}{4} a\).

3. 答案 (1)\(\sqrt{2}\)；(2)\(\sqrt{5}\)
   解析 (1)如图所示，在\(△ABD\)中，
   \(\because ∠BAD=∠BAC+∠DAC=30^{\circ} +45^{\circ} =75^{\circ}\) ，
   \(\therefore ∠ADB=60^{\circ}\) ，
   由正弦定理可得， \(\dfrac{A B}{\sin \angle A D B}=\dfrac{A D}{\sin \angle A B D}\)， \(A D=\dfrac{\sqrt{3} \sin 45^{\circ}}{\sin 60^{\circ}}=\sqrt{2}\)．
   (2)\(\because ∠ABC=∠ABD+∠DBC=45^{\circ} +75^{\circ} =120^{\circ}\)，\(∠BAC=∠BCA=30^{\circ}\) ，
   \(\therefore BC=AB=\sqrt{3}\)，\(\therefore AC=3\)．
   在\(△ACD\)中，由余弦定理得，\(CD^2=AC^2+AD^2-2AC⋅AD\cos ⁡∠DAC=5\)，
   即\(CD=\sqrt{5}\)(海里)
   答：\(AD=\sqrt{2}\)，\(C\)，\(D\)间的距离为\(\sqrt{5}\)海里．

4. 答案 (1)\(\sqrt{3}\) ；(2) \(\dfrac{5 \sqrt{7}}{7}\)
   解析 (1)由题意得：\(BE=1\)，\(∠ABC=120^{\circ}\) ，\(EA=\sqrt{21}\)，
   在\(△ABE\)中，\(\because AE^2=AB^2+BE^2-2AB⋅BE⋅\cos ⁡∠ABE\)，
   \(\therefore 21=AB^2+1+AB\)，解得\(AB=4\)百米
   \(\therefore S_{\triangle A B E}=\dfrac{1}{2} \times A B \times B E \times \sin \angle A B E=\dfrac{1}{2} \times 4 \times 1 \times \dfrac{\sqrt{3}}{2}=\sqrt{3}\)平方百米．
   (2)记\(∠AEB=α\)，
   在\(△ABE\)中， \(\dfrac{A B}{\sin \alpha}=\dfrac{A E}{\sin \angle A B E}\)，即 \(\dfrac{4}{\sin \alpha}=\dfrac{\sqrt{21}}{\dfrac{\sqrt{3}}{2}}\)，
   \(\therefore \sin \alpha=\dfrac{2 \sqrt{7}}{7}\)， \(\cos \alpha=\sqrt{1-\sin ^2 \alpha}=\dfrac{\sqrt{21}}{7}\)，
   当\(CH⊥DE\)时，水管长最短，
   在\(RtΔECH\)中，
   \(C H=C E \sin \angle H E C=2 \sin \left(\dfrac{2 \pi}{3}-\alpha\right)=2 \sin \dfrac{2 \pi}{3} \cos \alpha-2 \cos \dfrac{2 \pi}{3} \sin \alpha=\dfrac{5 \sqrt{7}}{7}\)百米

5. 答案 (1)\(3\sqrt{2}\) ；(2) \(D\)船在\(A\)岛北偏东\(25^{\circ}\)方向上，距离\(A\)岛\(3\sqrt{3}\)海里处．
   解析 (1)由题意可得\(∠ABC=105^{\circ}\)，\(∠BAC=45^{\circ}\)，\(AB=3\)，
   \(\therefore ∠ACB=30^{\circ}\)，
   在\(△ABC\)中，由正弦定理得 \(\dfrac{A B}{\sin \angle A C B}=\dfrac{B C}{\sin \angle B A C}\)，
   即 \(\dfrac{3}{\dfrac{1}{2}}=\dfrac{B C}{\dfrac{\sqrt{2}}{2}}\)，解得\(BC=3\sqrt{2}\)(海里)．
   (2)由题意可知\(CD=3\sqrt{2}\)，\(∠ACD=60^{\circ}\)，
   在\(△ABC\)中，由余弦定理得 \(A C=\sqrt{A B^2+B C^2-2 A B \cdot B C \cdot \cos \angle A B C}=3 \sqrt{2+\sqrt{3}}\)，
   在\(△ACD\)中，由余弦定理 \(A D=\sqrt{A C^2+C D^2-2 A C \cdot C D \cos \angle A C D}=3 \sqrt{3}\)，
   由正弦定理得： \(\dfrac{C D}{\sin \angle D A C}=\dfrac{A D}{\sin \angle A C D}\)，即 \(\dfrac{3 \sqrt{2}}{\sin \angle D A C}=\dfrac{3 \sqrt{3}}{\sin 60^{\circ}}\)，
   解得 \(\sin \angle D A C=\dfrac{\sqrt{2}}{2}\)，
   \(\therefore ∠DAC=45^{\circ}\)，
   \(\therefore D\)船在\(A\)岛北偏东\(25^{\circ}\)方向上，距离\(A\)岛\(3\sqrt{3}\)海里处．
    
    

分层练习

【A组---基础题】

1.如图，在河岸边有一点\(A\)，河对岸有一点\(B\)，要测量\(A\)，\(B\)两点之间的距离，先在岸边取基线\(AC\)，测得\(AC=120 m\)，\(∠BAC=45^{\circ}\)，\(∠BCA=75^{\circ}\)，求\(A\)，\(B\)两点间的距离．

 
 

2.如图，隔河看到两个目标，，但不能到达，在岸边选取相距\(\sqrt{3} km\)的，两点，并测得\(∠ACB=75^{\circ}\)，\(∠BCD=45^{\circ}\)，\(∠ADC=30^{\circ}\)，\(∠ADB=45^{\circ}\)(\(A\)，\(B\)，\(C\)，\(D\)在同一平面内)，求两个目标\(A\)，\(B\)之间的距离．

 
 

3.某市一棚户区改造用地平面示意图如图所示．该区域是半径为\(R\)的圆面，圆面的内接四边形\(ABCD\)是原棚户区建筑用地，测量可知\(AB=AD=4km\)，\(BC=6km\)，\(CD=2km\)．
  (1)求原棚户区建筑用地\(ABCD\)中对角线\(AC\)的长度；
  (2)请计算原棚户区建筑用地\(ABCD\)的面积．

 
 

4.如图，某市郊外景区内一条笔直的公路\(a\)经过三个景点\(A\)、\(B\)、\(C\)，景区管委会又开发了风景优美的景点\(D\)，经测量景点\(D\)位于景点\(A\)的北偏东\(30^{\circ}\)方向\(8km\)处，位于景点\(B\)的正北方向，还位于景点\(C\)的北偏西\(75^{\circ}\)方向上，已知\(AB=5km\)．
  (1)景区管委会准备由景点\(D\)向景点\(B\)修建一条笔直的公路，不考虑其他因素，求出这条公路的长；(结果精确到\(0.1km\))
  (2)求景点\(C\)与景点\(D\)之间的距离．(结果精确到\(0.1km\))

 
 

参考答案

1. 答案 \(20(3\sqrt{2}+\sqrt{6})\)
   解析 在\(△ABC\)中，\(AC=120 m\)，\(∠BAC=45^{\circ}\)，\(∠BCA=75^{\circ}\)
   则\(B=180^{\circ}-(A+C)=60^{\circ}\)，
   由正弦定理，
   得 \(A B=A C \dfrac{\sin C}{\sin B}=\dfrac{120 \sin 75^{\circ}}{\sin 60^{\circ}}=20(3 \sqrt{2}+\sqrt{6})\)．
   即\(A\)，\(B\)两点间的距离为\(20(3\sqrt{2}+\sqrt{6})m\).

2. 答案 \(\sqrt{5} km\)
   解析 在\(△ACD\)中，\(∠ADC=30^{\circ}\)，\(∠ACD=120^{\circ}\)，
   \(\therefore ∠CAD=30^{\circ}\)，
   \(\therefore AC=CD=\sqrt{3}\).
   在\(△BDC\)中，\(∠CBD=180^{\circ}-(45^{\circ}+30^{\circ}+45^{\circ})=60^{\circ}\).
   在\(△BCD\)中，由正弦定理，得 \(B C=\dfrac{\sqrt{3} \sin 75^{\circ}}{\sin 60^{\circ}}=\dfrac{\sqrt{6}+\sqrt{2}}{2}\).
   则在\(△ABC\)中，由余弦定理，得
   \(AB^2=AC^2+BC^2-2AC⋅BC⋅\cos ⁡∠BCA\)
   \(=(\sqrt{3})^2+\left(\dfrac{\sqrt{6}+\sqrt{2}}{2}\right)^2-2 \sqrt{3} \times \dfrac{\sqrt{6}+\sqrt{2}}{2} \cos 75^{\circ}=5\).
   \(\therefore AB=\sqrt{5}\).
   \(\therefore\) 两个目标\(A\)，\(B\)之间的距离为\(\sqrt{5} km\).

3. 答案 (1) \(2\sqrt{7} km\)；(2) \(8\sqrt{3} (km^2 )\)
   解析(1)由题意得\(\cos ⁡∠B=-\cos ⁡∠D\)，
   由余弦定理得，\(AC^2=4^2+6^2-2×4×6\cos ⁡B=4^2+2^2-2×2×4\cos ⁡∠D\)，
   所以 \(\cos \angle B=\dfrac{1}{2}\)，
   由\(B\)为三角形内角得，\(∠B=60^{\circ}\) ，\(∠D=120^{\circ}\)，
   故\(AC=2\sqrt{7} km\)；
   (2)由题意得四边形\(ABCD\)的面积 \(S=\dfrac{1}{2} \times 4 \times 6 \sin 60^{\circ}+\dfrac{1}{2} \times 2 \times 4 \sin 120^{\circ}=8 \sqrt{3}\left(\mathrm{~km}^2\right)\)．

4. 答案 (1) \(3.9km\)；(2) \(4km\)
   解析 (1)法1：在\(△DAB\)中，\(∠ADB=30^{\circ}\)，\(AD=8km\)，\(AB=5km\)，
   设\(DB=xkm\)，由余弦定理，得\(5^2=8^2+x^2-2×8x\cos 30^{\circ}\)，
   解得\(x=4\sqrt{3}-3≈3.9\)，\(\therefore\) 这条公路的长为\(3.9\)．
   法2：如图，过点\(D\)作\(DE⊥AC\)于点\(E\)，过点\(A\)作\(AF⊥DB\)，交\(DB\)的延长线于点\(F\)
   在\(Rt△DAF\)中，\(∠ADF=30^{\circ}\)， \(\therefore A F=\dfrac{1}{2} A D=\dfrac{1}{2} \times 8=4\)，
   \(\therefore D F=\sqrt{A D^2-A F^2}=\sqrt{8^2-4^2}=4 \sqrt{3}\)；
   在\(Rt△ABF\)中， \(B F=\sqrt{A B^2-A F^2}=\sqrt{5^2-4^2}=3\)，
   \(\therefore BD=DF-BF=4\sqrt{3}-3≈3.9\)，
   \(\therefore\)这条公路的长为\(3.9\)．
   (2) \(\sin \angle A B F=\dfrac{A F}{A B}=\dfrac{4}{5}\)，在\(Rt△DBE\)中， \(\sin \angle D B E=\dfrac{D E}{B D}\)，
   \(\because ∠ABF=∠DBE\)， \(\therefore \sin \angle D B E=\dfrac{4}{5}\)，
   \(\therefore D E=B D \cdot \sin \angle D B E=\dfrac{4}{5} \times(4 \sqrt{3}-3)=\dfrac{16 \sqrt{3}-12}{5} \approx 3.1(\mathrm{~km})\)
   由题意可知\(∠CDB=75^{\circ}\)，由(1)可知 \(\sin \angle D B E=\dfrac{4}{5}=0.8\)，
   所以\(∠DBE=53^{\circ}\)，
   \(\therefore ∠DCB=180^{\circ}-75^{\circ}-53^{\circ}=52^{\circ}\)
   在\(Rt△DCE\)中， \(\sin \angle D C E=\dfrac{D E}{D C}\)，
   \(\therefore D C=\dfrac{D E}{\sin 52^{\circ}} \approx \dfrac{3.1}{0.79} \approx 4(\mathrm{~km})\)
   \(\therefore\)景点\(C\)与景点\(D\)之间的距离约为\(4km\)．
    
    

【B组---提高题】

1.某校要在一条水泥路边安装路灯，其中灯杆的设计如图所示，\(AB\)为地面，\(CD\)，\(CE\)为路灯灯杆，\(CD⊥AB\)， \(\angle D C E=\dfrac{2 \pi}{3}\)，在 处安装路灯，且路灯的照明张角 \(\angle M E N=\dfrac{\pi}{3}\)．已知\(CD=4m\)，\(CE=2m\)．
  (1)当\(M\)，\(D\)重合时，求路灯在路面的照明宽度\(MN\)；
  (2)求此路灯在路面上的照明宽度\(MN\)的最小值．

 
 

2.如图所示，某镇有一块空地\(△OAB\)，其中\(OA=3km\)，\(OB=3\sqrt{3} km\)，\(∠AOB=90^{\circ}\)．当地镇政府规划将这块空地改造成一个旅游景点，拟在中间挖一个人工湖\(△OMN\)，其中\(M\)，\(N\)都在边\(AB\)上，且\(∠MON=30^{\circ}\)，挖出的泥土堆放在\(△OAM\)地带上形成假山，剩下的\(△OBN\)地带开设儿童游乐场．为安全起见，需在\(△OAN\)的一周安装防护网．
  (1)当 \(A M=\dfrac{3}{2} k m\)时，求防护网的总长度；
  (2)为节省投入资金，人工湖\(△OMN\)的面积要尽可能小，问如何设计施工方案，可使\(△OMN\)的面积最小？最小面积是多少？

 
 

参考答案

1. 答案 (1) \(\dfrac{7 \sqrt{3}}{2} m\)；(2) \(\dfrac{10 \sqrt{3}}{3} m\)
   解析(1)当\(M\)，\(D\)重合时，
   由余弦定理知， \(M E=D E=\sqrt{C D^2+C E^2-2 C D \cdot C E \cdot \cos \angle D C E}=2 \sqrt{7}\)，
   所以 \(\cos \angle C D E=\dfrac{C D^2+D E^2-C E^2}{2 C D \cdot D E}=\dfrac{5 \sqrt{7}}{14}\)，
   因为 \(\angle C D E+\angle E M N=\dfrac{\pi}{2}\)，
   所以 \(\sin \angle E M N=\cos \angle C D E=\dfrac{5 \sqrt{7}}{14}\)，
   因为\(\cos ⁡∠EMN>0\)，
   所以 \(\cos \angle E M N=\sqrt{1-\sin ^2 \angle E M N}=\dfrac{\sqrt{21}}{14}\)，
   因为 \(\angle M E N=\dfrac{\pi}{3}\)，
   所以 \(\sin \angle E N M=\sin \left(\dfrac{2 \pi}{3}-\angle E M N\right)=\sin \dfrac{2 \pi}{3} \cos \angle E M N-\cos \dfrac{2 \pi}{3} \sin \angle E M N=\dfrac{2 \sqrt{7}}{7}\)．
   \(\therefore\)在\(△EMN\)中，由正弦定理可知， \(\dfrac{M N}{\sin \angle M E N}=\dfrac{E M}{\sin \angle E N M}\)，
   解得 \(M N=\dfrac{7 \sqrt{3}}{2}\)；
   (2)易知\(E\)到地面的距离 \(h=4+2 \sin \left(\dfrac{2 \pi}{3}-\dfrac{\pi}{2}\right)=5 m\)，
   由三角形面积公式可知， \(S_{\triangle E M N}=\dfrac{1}{2} \cdot M N \cdot 5=\dfrac{1}{2} E M \cdot E N \cdot \sin \dfrac{\pi}{3}\)，
   所以 \(\dfrac{10}{\sqrt{3}} M N=E M \cdot E N\)，
   又由余弦定理可知，\(MN^2=EM^2+EN^2-2EM⋅EN⋅\cos ⁡\dfrac{\pi}{3}⩾EM⋅EN\)，
   当且仅当\(EM=EN\)时，等号成立，
   所以 \(M N^2 \geqslant \dfrac{10}{\sqrt{3}} M N\)，解得 \(M N \geqslant \dfrac{10 \sqrt{3}}{3}\)；
   答：(1)路灯在路面的照明宽度为\(\dfrac{7 \sqrt{3}}{2} m\)；(2)照明宽度\(MN\)的最小值为 \(\dfrac{10 \sqrt{3}}{3} m\)．

2. 答案 (1) \(9km\)；(2) \(\dfrac{27(2-\sqrt{3})}{4} k m^2\)
   解析(1)\(\because OA=3km\)，\(OB=3\sqrt{3} km\)，\(∠AOB=90^{\circ}\)，
   \(\therefore A=60^{\circ}\)，\(AB=6\)．
   在\(△OAM\)中，由余弦定理得\(O M^2=O A^2+A M^2-2 O A \cdot A M \cdot \cos A=\dfrac{27}{4}\)．
   \(\therefore O M=\dfrac{3 \sqrt{3}}{2}\)．
   由正弦定理得\(\dfrac{A M}{\sin \angle A O M}=\dfrac{O M}{\sin A}\)，即 \(\dfrac{\dfrac{3}{2}}{\sin \angle A O M}=\dfrac{\dfrac{3 \sqrt{3}}{2}}{\dfrac{\sqrt{3}}{2}}\)，
   \(\therefore \sin \angle A O M=\dfrac{1}{2}\)．\(\therefore A=30^{\circ}\)．
   \(\therefore ∠AON=∠AOM+∠MON=60^{\circ}\)．
   \(\therefore △OAN\)是等边三角形．
   \(\therefore △OAN\)的周长\(C=3OA=9\)．
   \(\therefore\) 防护网的总长度为\(9km\)．
   (2)设\(∠AOM=θ(0^{\circ}<θ<60^{\circ})\)，
   则\(∠AON=θ+30^{\circ}\)，\(∠OMA=120^{\circ}-θ\)，\(∠ONA=90^{\circ}-θ\)．
   在\(△OAM\)中，由正弦定理得 \(\dfrac{O M}{\sin A}=\dfrac{O A}{\sin \angle O M A}\)，
   即 \(\dfrac{O M}{\dfrac{\sqrt{3}}{2}}=\dfrac{3}{\sin \left(120^{\circ}-\theta\right)}=\dfrac{3}{\sin \left(60^{\circ}+\theta\right)}\)．
   \(\therefore O M=\dfrac{3 \sqrt{3}}{2 \sin \left(60^{\circ}+\theta\right)}\)，
   在\(△AON\)中，由正弦定理得 \(\dfrac{O N}{\sin A}=\dfrac{O A}{\sin \angle O N A}\)，
   即 \(\dfrac{O N}{\dfrac{\sqrt{3}}{2}}=\dfrac{3}{\sin \left(90^{\circ}-\theta\right)}=\dfrac{3}{\cos \theta}\)，
   \(\therefore O N=\dfrac{3 \sqrt{3}}{2 \cos \theta}\)，
   \(\therefore S_{\triangle O M N}=\dfrac{1}{2} O M \cdot O N \cdot \sin \angle M O N\)\(=\dfrac{27}{16 \cos \theta \sin \left(\theta+60^{\circ}\right)}=\dfrac{27}{8 \sin \left(2 \theta+60^{\circ}\right)+4 \sqrt{3}}\)．
   \(\therefore\)当且仅当\(2θ+60^{\circ}=90^{\circ}\)，即\(θ=15^{\circ}\)时，
   \(△OMN\)的面积取最小值为 \(\dfrac{27}{8+4 \sqrt{3}}=\dfrac{27(2-\sqrt{3})}{4} \mathrm{~km}^2\)．
    
    

【C组---拓展题】

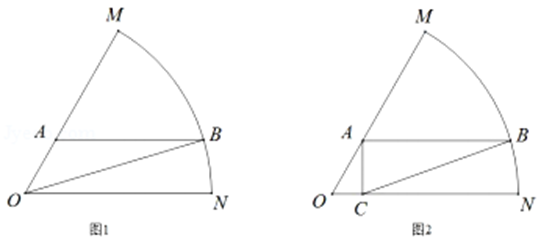
1.如图，已知扇形\(OMN\)是一个观光区的平面示意图，其中扇形半径为\(10\)米， \(\angle M O N=\dfrac{\pi}{3}\)，为了便于游客观光和旅游，提出以下两种设计方案：
  (1)如图\(1\)，拟在观光区内规划一条三角形\(ABO\)形状的道路，道路的一个顶点\(B\)在弧\(MN\)上，另一顶点\(A\)在半径\(OM\)上，且\(AB∥ON\)，求\(△ABO\)周长的最大值；
  (2)如图\(2\)，拟在观光区内规划一个三角形区域种植花卉，三角形花圃\(ABC\)的一个顶点\(B\)在弧\(MN\)上，另两个顶点\(A\)、\(C\)在半径\(OM\)、\(ON\)上，且\(AB∥ON\)，\(AC⊥ON\)，求花圃\(△ABC\)面积的最大值．

 
 
 
 

参考答案

1. 答案 (1) \(\dfrac{20 \sqrt{3}}{3}+10\)米 ；(2) \(\dfrac{25 \sqrt{3}}{3}\)平方米
   解析(1)\(\because AB∥ON\)， \(\angle M O N=\dfrac{\pi}{3}\)， \(\therefore \angle O A B=\dfrac{2 \pi}{3}\)，
   又\(OB=10\)，设 \(\angle M O B=\theta， \theta \in\left(0， \dfrac{\pi}{3}\right)\)，
   在\(△AOB\)中，由正弦定理可知， \(\dfrac{O B}{\sin \angle O A B}=\dfrac{A B}{\sin \theta}=\dfrac{O A}{\sin \left(\dfrac{\pi}{3}-\theta\right)}=\dfrac{10}{\dfrac{\sqrt{3}}{2}}=\dfrac{20 \sqrt{3}}{3}\)，
   \(\therefore A B=\dfrac{20}{\sqrt{3}} \sin \theta\)，\(O A=\dfrac{20}{\sqrt{3}} \sin \left(\dfrac{\pi}{3}-\theta\right)\)
   \(\therefore △AOB\)的周长 \(f(\theta)=\dfrac{20}{\sqrt{3}}\left[\sin \theta+\sin \left(\dfrac{\pi}{3}-\theta\right)\right]+10， \quad \theta \in\left(0， \dfrac{\pi}{3}\right)\)．
   化简得 \(f(\theta)=\dfrac{20}{\sqrt{3}} \sin \left(\theta+\dfrac{\pi}{3}\right)+10\)．
   \(\therefore \theta=\dfrac{\pi}{6}\)时，\(△AOB\)的周长有最大值为\(\dfrac{20 \sqrt{3}}{3}+10\)米．
   答：\(△ABO\)周长的最大值为\(\dfrac{20 \sqrt{3}}{3}+10\)米；
   (2)\(\because\)图\(2\)中\(△ABC\)与图\(1\)中\(△ABO\)面积相等，
   而在\(△ABO\)中，\(\because OB=r=10\)，\(AB∥ON\)， \(\angle M O N=\dfrac{\pi}{3}\)，
   \(\therefore \angle O A B=\dfrac{2 \pi}{3}\)．
   由余弦定理知，\(OB^2=OA^2+AB^2-2OA\cdot AB\cdot \cos ∠OAB\)，
   \(\therefore 100=OA^2+AB^2+OA\cdot AB≥3OA\cdot AB\)，
   \(\therefore O A \cdot A B \leq \dfrac{100}{3}\)，当且仅当 \(O A=A B=\dfrac{10}{\sqrt{3}}=\dfrac{10 \sqrt{3}}{3}\)时取\(“=”\)．
   \(\therefore S_{\triangle A B C}=\dfrac{1}{2} O A \cdot A B \cdot \sin 120^{\circ} \leq \dfrac{1}{2} \times \dfrac{100}{3} \times \dfrac{\sqrt{3}}{2}=\dfrac{25 \sqrt{3}}{3}\)平方米．
   答：花圃\(△ABC\)面积的最大值为\(\dfrac{25 \sqrt{3}}{3}\) 平方米，此时 \(O A=O B=\dfrac{10 \sqrt{3}}{3}\)米．