数字三角形模型
数字三角形模型
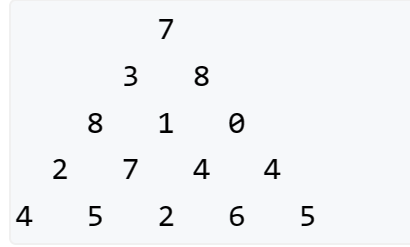
给定一个如下图所示的数字三角形,从顶部出发,在每一结点可以选择移动至其左下方的结点或移动至其右下方的结点,一直走到底层,要求找出一条路径,使路径上的数字的和最大。
状态表示:\(f[i][j]\)代表从\((1,1)\)到\((i,j)\)的路径和最大值
状态属性:\(MAX\)
状态计算:\((i,j)\)可以由\((i-1,j-1)和(i-1,j)\)转移
\[f[i][j]=max(f[i-1][j],f[i-1][j-1])+a[i][j] \]状态初始:初始化为\(-INF\), \(f[1][1] = a[1][1]\)
答案呈现:\(\sum max(f[n][i])\)
const int N = 5e2 + 10;
int dp[N][N];
int a[N][N];
void slove()
{
int n;
cin >> n;
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= i; ++j)
cin >> a[i][j];
for (int i = 0; i <= n; ++i)
for (int j = 0; j <= i + 1; ++j)
dp[i][j] = -INF;
dp[1][1] = a[1][1];
for (int i = 2; i <= n; ++i)
for (int j = 1; j <= i; ++j)
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - 1]) + a[i][j];
int ans = -INF;
for (int i = 1; i <= n; ++i)
ans = max(ans, dp[n][i]);
cout << ans << endl;
}
摘花生
给定一个 \(n \times m\) 的矩阵,矩阵中每个元素的值非负,现在你需要从矩阵的左上角\((1,1)\)到右下角\((n,m)\),每一步只能向右或向下走,请你找到一条路径使得该路径上经过的元素的和最大,请你求出最大的和
\(1 \le n,m \le 100\)
题解:线性DP \(O(n^2)\)
- 状态表示:
\(f[i][j]\)代表从起点\((1,1)\)到\((i,j)\)的所有路径中的元素之和最大值
状态属性:\(MAX\)
状态计算:按照最后一步从上面或者左边过来进行划分
- 最后一步从上面过来:\(f[i-1][j]\)
- 最后一步从左边过来:\(f[i][j-1]\)
\[f[i][j] = max(f[i-1][j],f[i][j-1])+a[i][j] \]
状态初始:\(f[1][1] = a[1][1],f[i][j] = 0\)
答案呈现:\(f[n][m]\)
const int N = 1e2 + 10;
int n, m;
int a[N][N];
int f[N][N];
void solve()
{
cin >> n >> m;
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j)
{
cin >> a[i][j];
f[i][j] = 0;
}
f[1][1] = a[1][1];
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j)
f[i][j] = max(f[i - 1][j] + a[i][j], f[i][j - 1] + a[i][j]);
cout << f[n][m] << endl;
}
最低通行费
一个商人穿过一个 \(N×N\) 的正方形的网格,去参加一个非常重要的商务活动。
他要从网格的左上角进,右下角出。
每穿越中间 \(1\) 个小方格,都要花费 \(1\) 个单位时间。
商人必须在 \((2N−1)\) 个单位时间穿越出去。
而在经过中间的每个小方格时,都需要缴纳一定的费用。
这个商人期望在规定时间内用最少费用穿越出去
\(1 \le n \le 100\)
题解:线性DP \(O(n^2)\)
我们发现这名商人最少从这个正方形网格中穿出去的时间都需要\(2N-1\)个单位,说明他不能走回头路,只能往下或者往右走,那么这道题又等价于上面那题摘花生了,\(dp\)过程不再赘述
const int N = 1e2 + 10;
int n;
int a[N][N];
int f[N][N];
void solve()
{
cin >> n;
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
cin >> a[i][j];
for (int i = 0; i <= n; ++i)
for (int j = 0; j <= n; ++j)
f[i][j] = INF;
f[1][1] = a[1][1];
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
f[i][j] = min({f[i][j], f[i - 1][j] + a[i][j], f[i][j - 1] + a[i][j]});
cout << f[n][n] << endl;
}
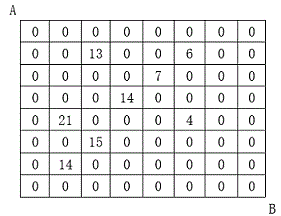
方格取数
设有 \(n×n\) 的方格图,我们在其中的某些方格中填入正整数,而其它的方格中则放入数字\(0\)。如下图所示:
某人从图中的左上角 \(A\) 出发,可以向下行走,也可以向右行走,直到到达右下角的 \(B\) 点
在走过的路上,他可以取走方格中的数(取走后的方格中将变为数字\(0\))
此人从 \(A\) 点到 \(B\) 点共走了两次,试找出两条这样的路径,两条路径上的点可以重复,使得取得的数字和为最大
\(1 \le n \le 10\)
题解:线性DP \(O(n^3)\)
- 状态表示:\(O(n^4)\)
\(f[i_1][j_1][i_2][j_2]\)代表所有从\((1,1)\)到\((i_1,j_1)\)和从\((1,1)\)到\((i_2,j_2)\)的两条路线中数字之和的最大值
状态属性:\(MAX\)
状态计算:可以从上或者从左到\((i_1,j_1)\),可以从上或者从左到\((i_2,j_2)\),那么一共有\(2 \times 2 = 4\)种选择 \(O(1)\)
- 从左边到\((i_1,j_1)\),从左边到\((i_2,j_2)\):\(f[i_1][j_1-1][i_2][j_2-1]\)
- 从左边到\((i_1,j_1)\),从上边到\((i_2,j_2)\):\(f[i_1][j_1-1][i_2-1][j_2]\)
- 从上边到\((i_1,j_1)\),从左边到\((i_2,j_2)\):\(f[i_1-1][j_1][i_2][j_2-1]\)
- 从上边到\((i_1,j_1)\),从上边到\((i_2,j_2)\):\(f[i_1-1][j_1][i_2-1][j_2]\)
注意:如果\((i_1,j_1)\) = \((i_2,j_2)\),那么我们只能取一次该位置上的数字
\[f[i_1][j_1][i_2][j_2] = max({f[i_1 - 1][j_1][i_2 - 1][j_], f[i_1 - 1][j_1][i_2][j_2 - 1], f[i_1][j_1 - 1][i_2 - 1][j_2], f[i_1][j_1 - 1][i_2][j_2 - 1]}) + g[i_1][j_1] \\ (i_1,j_1) ==(i_2,j_2) \]\[f[i_1][j_1][i_2][j_2] = max({f[i_1 - 1][j_1][i_2 - 1][j_], f[i_1 - 1][j_1][i_2][j_2 - 1], f[i_1][j_1 - 1][i_2 - 1][j_2], f[i_1][j_1 - 1][i_2][j_2 - 1]}) + g[i_1][j_1]+g[i_2][j_2] \\ (i_1,j_1)\neq(i_2,j_2) \]
- 状态优化:\(O(n^3)\)
我们发现只有步数一样的时候两条路线才有可能重合,设走过的步数为\(k\),那么如果\(i_1=i_2\),就说明两条路线在这个点重合了,该点坐标为\((i_1,k-i_1)\),所以我们可以将状态合并为:
\(f[k][i_1][i_2]\)代表经过\(k\)步后,一条路线现在经过的点的横坐标为 \(i_1\),另一条路线现在经过的点的横坐标为\(i_2\),两条路线中数字之和的最大值
状态计算和上面一样,不再赘述
状态初始:\(f[2][1][1] = g[1][1]\)
答案呈现:\(f[2 * n][n][n]\)
const int N = 12, M = 4e5 + 10;
int n;
int g[N][N];
int f[N << 1][N][N];
void solve()
{
cin >> n;
int a, b, c;
while (cin >> a >> b >> c, a || b || c)
{
g[a][b] = c;
}
f[2][1][1] = g[1][1];
for (int k = 3; k <= 2 * n; ++k)
for (int i1 = 1; i1 <= n; ++i1)
for (int i2 = 1; i2 <= n; ++i2)
{
int j1 = k - i1, j2 = k - i2;
if (j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n)
{
if (i1 == i2)
f[k][i1][i2] = max({f[k - 1][i1 - 1][i2 - 1], f[k - 1][i1][i2 - 1], f[k - 1][i1 - 1][i2], f[k - 1][i1][i2]}) + g[i1][j1];
else
f[k][i1][i2] = max({f[k - 1][i1 - 1][i2 - 1], f[k - 1][i1][i2 - 1], f[k - 1][i1 - 1][i2], f[k - 1][i1][i2]}) + g[i1][j1] + g[i2][j2];
}
}
cout << f[2 * n][n][n] << endl;
}
传纸条
给定一个 \(n \times m\) 的矩阵,矩阵中每个元素的值非负,现在你需要从矩阵的左上角\((1,1)\)到右下角\((n,m)\),每一步只能向右或向下走,然后再从矩阵的右下角\((n,m)\)到左上角\((1,1)\),每一步只能向左或向上走,且之前经过的点不能再经过,请你找到一条路径使得该路径上经过的元素的和最大,请你求出最大的和
题解:线性DP
不难发现任意一条从矩阵的右下角\((n,m)\)到左上角\((1,1)\)的路线都能将其方向反转后变成从矩阵的左上角\((1,1)\)到右下角\((n,m)\)的一条路线,且经过的点不变
所以我们可以将题目转化为从矩阵的左上角\((1,1)\)到右下角\((n,m)\)走两次,每一步只能向右或向下走,且第二次走的路线中的点不能和第一次经过的点有交集
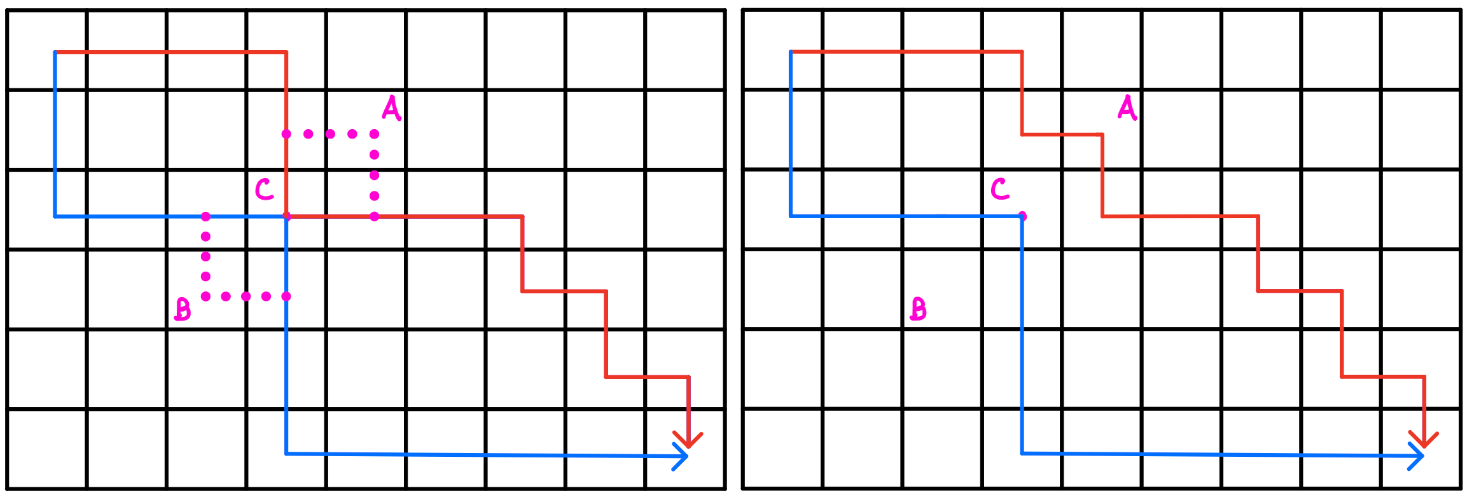
那么实际上已经和方格取数的\(dp\)模型非常接近了,我们只要解决两次经过的点不存在交集的问题即可,那么实际上我们可以证明方格取数的\(dp\)模型在这道题同样适用于解决两次经过的点不存在交集的问题,下面请看证明:
如果两条最优线路是交叉的
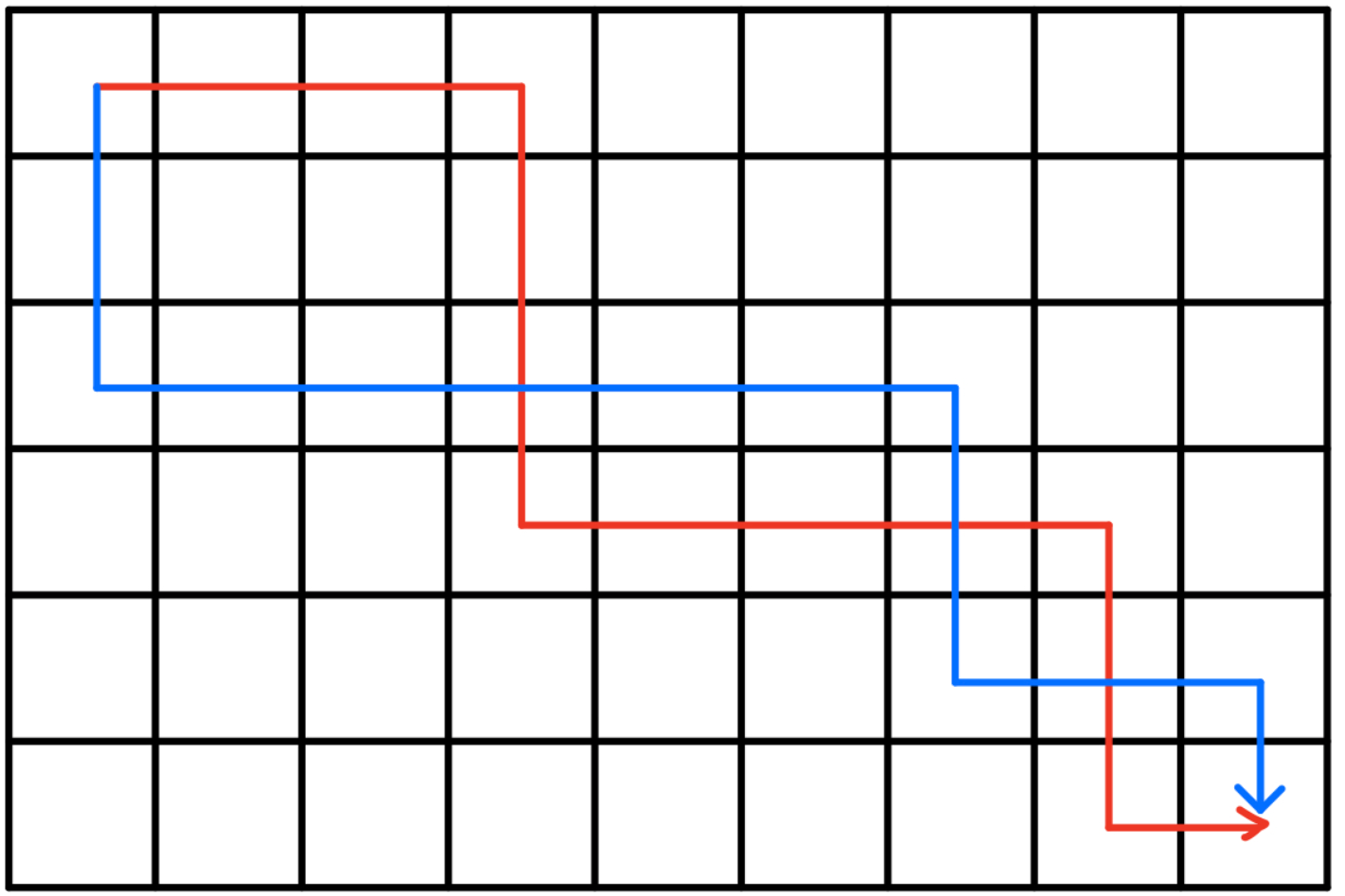
我们可以将其交叉的部分进行交换变成:
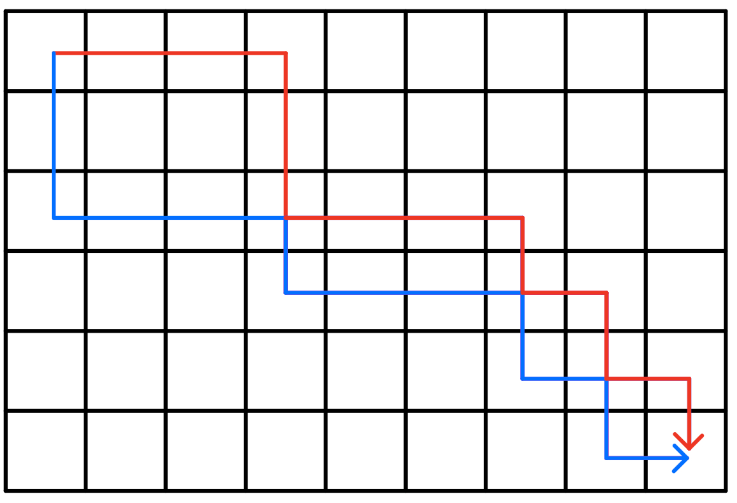
所以所有存在交叉的最优线路都能转化为存在交点的两条路线,我们只需要考虑如何解决两条路线不交叉,但是存在交点的情况
根据最优路线我们知道\(w_A=w_B=0\),所以我们可以微调其中一条路线,使得两条路径不经过重合点,且不影响路线的最优性
const int N = 55, M = 4e5 + 10;
int n, m;
int g[N][N];
int f[N << 1][N][N];
void solve()
{
cin >> n >> m;
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j)
cin >> g[i][j];
f[2][1][1] = g[1][1];
for (int k = 3; k <= n + m; ++k)
for (int i1 = 1; i1 <= n; ++i1)
for (int i2 = 1; i2 <= n; ++i2)
{
int j1 = k - i1, j2 = k - i2;
if (j1 >= 1 && j1 <= m && j2 >= 1 && j2 <= m)
{
if (i1 == i2)
f[k][i1][i2] = max({f[k - 1][i1 - 1][i2 - 1], f[k - 1][i1][i2 - 1], f[k - 1][i1 - 1][i2], f[k - 1][i1][i2]}) + g[i1][j1];
else
f[k][i1][i2] = max({f[k - 1][i1 - 1][i2 - 1], f[k - 1][i1][i2 - 1], f[k - 1][i1 - 1][i2], f[k - 1][i1][i2]}) + g[i1][j1] + g[i2][j2];
}
}
cout << f[n + m][n][n] << endl;
}