LeetCode 双指针
15. 三数之和 (为0)
下标不能是重复的,必定右 i<l<r
1、先对数组排序(从小到大)
2、外层 i 遍历
-
- 如果 nums[i] > 0 ,整个 nums[] 后面的必定无法有三元组为0(排过序了,后面的 nums[l] nums[r] 都会大于0)。break。
- 如果 nums[i] = nums[i-1] 即当前这个值已经在前一个算过了,这个的答案是包含于前一个的,不用搞了。continue。
3、对于 nums[i] 后面的那段,用左右指针,l = i+1; r = len-1 往中间
三数之和 = nums[i] + nums[l] + nums[r]
-
- 如果三数之和小于0,那么左指针向右,右指针不动,使和变大
- 如果三数之和大于0,那么左指针不动,右指针向左,使和变小
- 如果三数之和等于0
- while nums[l] = nums[l+1] l++ 左指针和它右边的一样了,那它右边的可以直接替换掉它,不然会重复
- while nums[r] = nums[r-1] r-- 右指针和它左边的一样了,那它左边的可以直接替换掉它,不然会重复
- 添加结果,同时这个结果已经有了,那么继续往下走,l++; r--
class Solution { public List<List<Integer>> threeSum(int[] nums) { List<List<Integer>> result = new ArrayList(); // 先从小到大排序,注意对数组的排序用 Arrays.sort Arrays.sort(nums); int len = nums.length; // 为了确保不重复 i<r<l for (int i=0;i<len;i++) { // 已经排过序了,nums[i]>0 必定无法有三元组(后面的 j,k 都会大于 0) if (nums[i]>0) { break; } // 对于 -4 -1 -1 0 1 2, 第一个 -1 就已经把 -1,-1,2 和 -1,0,1 两个答案搞出来了 // 后面那个 -1 不用再继续搞了,必定被包含在前一个 -1 的答案集中,且答案集比前一个 -1 的答案集小 if (i != 0 && nums[i] == nums[i-1]) { continue; } // 对于 i 右边这段左右指针进行操作 // 左指针 int l = i+1; // 右指针 int r = len-1; while(l<r) { int sum = nums[i] + nums[l] + nums[r]; if (sum == 0) { // 左指针和它右边的一样了,那它右边的可以直接替换掉它。不替换的话会重复 // 注意加限制 l<r while (l<r && nums[l] == nums[l+1]) { l++; } // 右指针和它左边的一样了,那它左边的可以直接替换掉它。不替换的话会重复 // 注意加限制 l<r while (l<r && nums[r] == nums[r-1]) { r--; } result.add(Arrays.asList(nums[i], nums[l], nums[r])); // 添加完结果,别忘了继续移动左右执政 l++; r--; } // 左指针向右,右指针不动。可使和变大 else if (sum<0) { l++; } // 左指针不动,右指针向左,可使和变小 else if (sum>0) { r--; } } } return result; } }
26. 删除有序数组中的重复项
就是将不重复的元素复制到数组的左边
双指针:l r
如果 nums[l] == nums[r] 那么 r 继续向右寻找不与 nums[l] 相等的元素
如果 nums[l] != nums[r] 那么把这个不相等的 nums[r] 复制到 l 的右边。同时 l 和 r 同时向右移动。
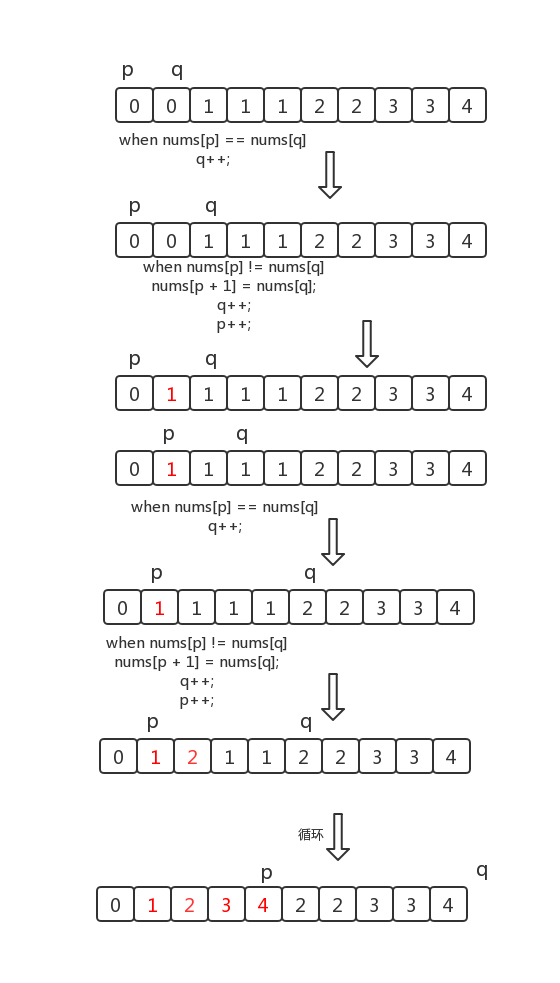
class Solution { public int removeDuplicates(int[] nums) { // 左指针 int index1=0; // 右指针负责找不重复的,不重复的话把不重复的依次复制到左指针的右边(占据重复元素的位置) int index2=0; while(index2 < nums.length) { // index2 右指针找到的都是重复的,那么继续向右找 if (nums[index1] == nums[index2]) { index2 = index2 + 1; } // 找到不重复的复制到左指针的右边 else { // 考虑 1,2,3,4 如果左右指针挨着,说明它们之间本来就没有重复的,不用多赋值一遍 if (index2 - index1>1) { nums[index1+1] = nums[index2]; } index1 = index1 + 1; index2 = index2 + 1; } } return index1 + 1; } }
56. 合并区间
输入:intervals = [[1,3],[2,6],[8,10],[15,18]] 输出:[[1,6],[8,10],[15,18]]
先按左边界排序,然后左右指针遍历新数组。左指针:上一个区间; 右指针:当前区间
如果当前区间左边界小于等于上一个区间的右边界,则说明是重叠边界,更新当前区间的左右边界,将当前区间的左右边界扩展为重叠区间的最大;
如果当前区间的左边界大于上一个区间的右边界,则将上一个区间放入结果数组。
遍历完毕,再将数组最后一个区间放入结果数组。
class Solution { public int[][] merge(int[][] intervals) { // 注意这里怎么根据起始元素排序 Arrays.sort(intervals, (e1, e2)->e1[0]-e2[0]); // 结果数组长度先设为和 intervels 一样 int[][] res = new int[intervals.length][2]; // 左指针 int l = 0; // 右指针 int r = 1; // 结果数组现在复制到哪儿了 int resNowIndex = 0; // l<r 为了使得最后一个元素能被复制,判断条件是 l while(l < intervals.length) { // 重叠区间:右指针区间的起始小于等于左指针区间的结束 [1,"3"]["2",6][8,10] if (r < intervals.length && intervals[r][0] <= intervals[l][1]) { // 将右指针的区间更新为融合了左边界之后的最大 [1,3][2,6][8,10]-->[1,3][1,6][8,10] if (intervals[r][1] >= intervals[l][1]) { intervals[r][0] = intervals[l][0]; } // 注意 [1,4][2,3] 要合并成 [1,4] else if (intervals[r][1] < intervals[l][1]) { intervals[r][0] = intervals[l][0]; intervals[r][1] = intervals[l][1]; } } else { // 不是重叠区间,就将上一个结果放到答案中,将 [1,6] 放到答案中 res[resNowIndex][0] = intervals[l][0]; res[resNowIndex][1] = intervals[l][1]; resNowIndex++; } r++; l++; } // 注意怎么去掉数组多出来的0 return Arrays.copyOf(res, resNowIndex); } }