麻将游戏
题目背景
在一种"麻将"游戏中,游戏是在一个有 \(w\times h\) 格子的矩形平板上进行的。每个格子可以放置一个麻将牌,也可以不放(如图所示)。玩家的目标是将平板上的所有可通过一条路径相连的两张相同的麻将牌,从平板上移去。最后如果能将所有牌移出平板,则算过关。
题目描述
这个游戏中的一个关键问题是:两张牌之间是否可以被一条路径所连接,该路径满足以下两个特性:
1. 它由若干条线段组成,每条线段要么是水平方向,要么是垂直方向。
2. 这条路径不能横穿任何一个麻将牌 (但允许路径暂时离开平板)。
这是一个例子:
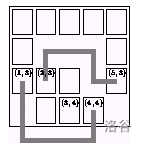
在 \((1,3)\) 的牌和在 \((4,4)\) 的牌可以被连接。 \((2,3)\) 和 \((3,4)\) 不能被连接。
你的任务是编一个程序,检测两张牌是否能被一条符合以上规定的路径所连接。
输入格式
1、输入文件的第一行有两个整数 \(w,h\) ,表示平板的宽和高。
2、接下来 \(h\) 行描述平板信息,每行包含 \(w\) 个字符,如果某格子有一张牌,则这个格子上有个 \('X'\) ,否则是一个空格。平板上最左上角格子的坐标为 \((1,1)\) ,最右下角格子的坐标为 \((w,h)\) 。
3、 接下来的若干行,每行有四个数 \(x1\), \(y1\) , \(x2\) , \(y2\) ,且满足 \(1<=x1,x2<=w\) , \(1<=y1,y2<=h\) ,表示两张牌的坐标(这两张牌的坐标总是不同的)。
4、如果出现连续四个 \(0\) ,则表示输入结束。
输出格式
输出文件中,对于每一对牌输出占一行,为连接这一对牌的路径最少包含的线段数。如果不存在路径则输出 \(0\) 。
样例输入
5 4
XXXXX
X X
XXX X
XXX
2 3 5 3
1 3 4 4
2 3 3 4
0 0 0 0
样例输出
4
3
0
提示
对于 \(100\%\) 的数据满足于:
$1<=w,h<=75 $
$1<=x1,x2<=w $
\(1<=y1,y2<=h\)
我们让要连接的两个麻将分别记为:\(A\) 与 \(B\) ,问题便转化成从 \(A\) 到 \(B\) 需要转几个弯,再把这个问题的答案加一即是最终答案
对于任意点 \(N\) ,它有四个方向可以移动,而这四个方向的所有点与 \(A\) 的连线数都是 \(N\) 的连线数加一(这里是保证了四个方向上的点下一次必定转弯)
那如果没转弯呢,那这个点肯定是上一个点访问过的点,直接忽略它
很明显的变式 \(bfs\)
最后还有这阴间的输入,看代码自行体会吧
\(Code:\)
#include<bits/stdc++.h>
using namespace std;
int n,m;
const int N=85;
const int dx[4]={1,-1,0,0};
const int dy[4]={0,0,1,-1};
int a[N][N],vis[N][N];
struct node{
int x,y,ans;
};
void bfs(int ax,int ay,int bx,int by){
int ans;memset(vis,0,sizeof(vis));//初始化一定要记得
queue<node> q;q.push((node){ax,ay,0});
while(q.size()){
node x=q.front();q.pop();
if(x.x==bx&&x.y==by){
printf("%d\n",x.ans);
return ;
}
for(int i=0;i<4;i++){
int nx=x.x+dx[i],ny=x.y+dy[i];
while(nx>=0&&nx<=n+1&&ny>=0&&ny<=m+1&&!a[nx][ny]){
if(!vis[nx][ny]) vis[nx][ny]=1,q.push((node){nx,ny,x.ans+1});//通过vis来判断是否被访问过
nx+=dx[i],ny+=dy[i];
}
}
}
printf("0\n");
}
int main()
{
scanf("%d%d",&m,&n);//要反过来
for(int i=1;i<=n;i++){
char c=getchar();
for(int j=1;j<=m;j++){
c=getchar();
if(c==' ') a[i][j]=0;
else a[i][j]=1;
}
}
int ax,ay,bx,by;
scanf("%d%d%d%d",&ax,&ay,&bx,&by);
while(ax||ay||bx||by){
a[by][bx]=0;//记得把终点变成空气,否则找不到终点
bfs(ay,ax,by,bx);
a[by][bx]=1;
scanf("%d%d%d%d",&ax,&ay,&bx,&by);
}
return 0;
}