5 月训练记录
[POI2017]Turysta
学习了竞赛图构造汉密尔顿回路。
首先对竞赛图缩点,最终拓扑序一定是一条链。考虑如何在一个强连通竞赛图中构造汉密尔顿回路。
首先,我们尝试构造汉密尔顿通路。考虑增量构造。我们一个个地加点,设当前加入的点为 \(x\),当前构造好的路径为 \(s\) 到 \(t\),那么我们分类讨论:
- 若 \(x\to s\),我们直接让 \(x\) 连接 \(s\),\(s:=x\);
- 若 \(t\to x\),我们直接让 \(t\) 连接 \(x\),\(t:=x\);
- 现在我们只剩下 \(s\to x\),\(x\to t\) 的情况,于是考虑链上一定存在一个点 \(y\) 以及 \(y\) 连接的点 \(z\),满足 \(y\to x\),\(x\to z\)。于是直接在 \(y\to z\) 中插入 \(x\) 即可。
考虑多次进行这个过程,每次对点 shuffle,即可获得 \(98\) 分,当然这样确实是可以卡的。
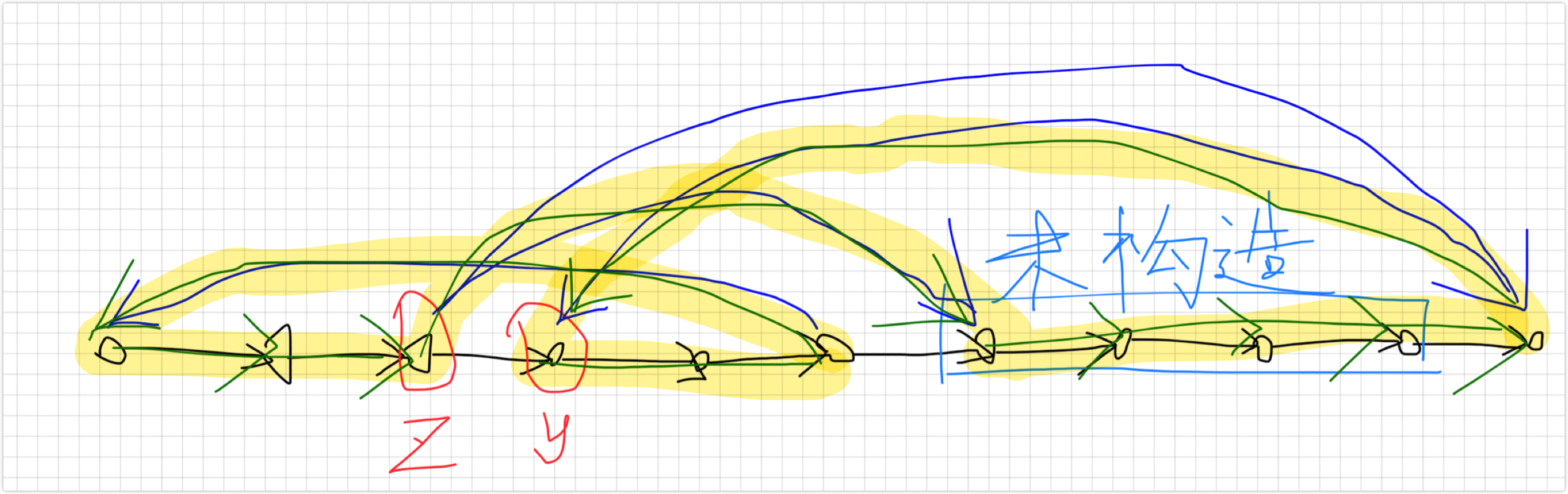
接着我们考虑构造汉密尔顿通路。我们依旧考虑增量构造(但不是纯增量构造)。设当前加入的点为 \(x\),当前构造好的环起点为 \(s\),我们依旧分类讨论:
- 若 \(x\to s\),那么我们直接按照汉密尔顿通路并加入 \(x\to s\) 的边即可;
- 若存在点 \(x\to y\),\(y\) 在已经构造好的环中,我们找到从 \(s\) 开始往后第一个这样的点,设环中 \(z\to y\)。由于我们找的是第一个,并且 \(s\to x\),所以,一定有 \(z \to x\)。于是就可以构造了。
- 若不存在情况 2,则我们把这个点留下,并在之后一起构造。
情况 2、3 的构造:
时间复杂度 \(O(n^2)\)。
记录。