qbxt day1

朝气蓬勃后生可畏 / 2023-05-03 / 原文

数学知识

现有奇数个人，两两间可能认识或不认识，请证明永远存在一个认识偶数个人的人。

将其转化成更强的问题: 给定一张奇数个点的图 \(G\) ，证明度数为偶数的点的个数为
奇数。
继续考虑它的相反的问题: 给定一张奇数个点的图 \(G\) ，证明度数为奇数的结点的个数为偶数
考虑所有点的度数和，由于一条边会被计算到两个结点的度数上，故其必定为偶数。

证明一个 \(n\) 个点和至少 \(\dfrac{(n - 1)(n - 2)}{2}\) 条边的图是连通图。

有 \(n - 1\) 个点的连通图至多有 \(\dfrac{(n - 2)(n - 1)}{2}\) 个点，所以可以证得 \(n\) 个点和至少 \(\dfrac{(n - 1)(n - 2)}{2}\) 条边的图是连通图。

欧拉回路：点的度数都为偶数的图存在欧拉回路。
欧拉通路：不存在或存在 \(2\) 个度数为奇数的图存在欧拉通路。
哈密顿回路：每个点只经过一次的回路。

若每个点的度数大于等于 \(\dfrac{n}{2}\)，则必定存在哈密顿回路。
若两个不相邻的点的度数和大于 \(n\)，则必定存在哈密顿回路。

反证法，假设 \(G\) 没有哈密顿回路。
我们由图 \(G\) 构造出一个新的没有哈密顿回路的图 \(G'\)，具体的，令 \(G' = G\) ，对于每条不在图 \(G\) 中的边，如果加入 \(G'\) 后不会产生哈密顿回路，则加入，该构造的顺序不重要。
此时我们得到了一个图 \(G\) ，再加入任何一条边都会得到一条哈密顿回路，并且由于我们仅加入了新的边，所有结点的度数任然大于等于 \(\dfrac{n}{2}\) 。
假设 \((v_1, v_n)\) 这条边不在 \(G'\) 中，我们知道必定存在一条哈密顿路径 \(v_1, v_2, v_3, \cdots, v_n\)，考虑 \((v_1, v_i)\) 有一条边，则 (v_{i - 1}, v_n) 必定不能有边，否则可以构造出一条哈密顿回路。
因为这样的 \(v_i\) 至少有 \(\dfrac{n}{2}\) 个，从而这样的 \(v_{i - 1}\) 也至少有 \(\dfrac{n}{2}\) 个，又由于 \(v_n\) 不能和自己连边，故而它至多与 \(n - \dfrac{n}{2} - 1\) 个点连边，但 \(deg(v_n) \ge \dfrac{n}{2}\) ，矛盾。

Posa 12岁的时候，他在餐桌上花费了半分钟证明出了这个问题。现有 \(n + 1\) 个小于等于 \(2n\) 的正整数，证明存在两个数互质。

两个相邻的数一定互质，根据鸽巢原理，一定有至少两个数是相邻的，所以存在两个数互质。

证明 \(G\) 或者 \(G\) 的补图至少有一个是连通的。

将点分成 \(k\) 个连通块，补图就是将不同连通块的点之间相互连边，由于原来连通块里的点都连接到了相同的点上（这个点在其他连通块上），这个可以保证原来的连通块里的点依然联通，所以，补图是联通的。

连通图 \(G\) 满足任意两条边至少有一个点是重合的，证明 \(G\) 要么是 \(3\) 个点的完全图，要么是星星。

假设 \(G\) 不是三个点的完全图，

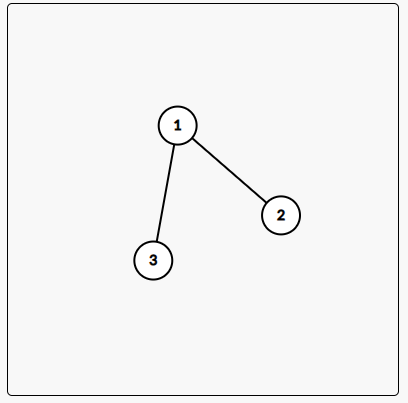
如图，若要加入一个新的点，要想满足条件，只能将边连向 \(1\) 点构成菊花，否则这个点会与 \(2\) 或 \(3\) 重合，同时连边构成三个点的完全图。

房间里有 \((m - 1)n + 1\) 个人，证明要么存在 \(m\) 个人两两不认识，要么存
在一个人认识至少 \(n\) 个人。

假设不存在一个人至少认识 \(n\) 个人，则每个联通块的点数最大为 \(n - 1\)。
原式可以转化为 \((n - 1)(m - 1) + m\)，可以看做有 \(m\) 个连通块，第 \(m\) 个连通块有 \(m\) 个点，每次从不同连通块中取一个人，则存在 \(m\) 个人两两不认识。

证明任意连通图 \(G\) 存在一个点 \(x\)，删掉后剩下的图依旧是连通图。

若图中有度数为 \(1\) 的点，则删掉这个点即可；没有度数为 \(1\) 的，任选一个点，删掉距离它最远的点即可。

现在有一张 \(4 \times n\) 的棋盘上有一个马(中国象棋)，证明不存在一条经过所有格子恰好一次并回到起点的路径。

将棋盘染色，同种颜色的不能挨着（就是染成像国际象棋的棋盘那样），马每走一步都要换色，同时将第一行、第四行染成蓝色，第二行、第三行染成红色，则蓝色下一步一定到红色，但红色下一步不一定到蓝色，为了保证走过所有的点，且每个点只走一遍，我们让红色下一步就到蓝色，则跳的顺序就是：黑蓝 \(\rightarrow\) 白红 \(\rightarrow\) 黑蓝。。。
但是，只有 \(2n\) 个点是黑蓝或白红，一共有 \(4n\) 个点，矛盾，证得。

图的存储

邻接矩阵
链式前向星
vector

二分图

称一张图 \(G = (V, E)\) 是二分图当且仅当点集 \(V\) 可以分为两半 \(A, B\) ，使得所有边都可以写成 \((a, b) \in E, a \in A, b \in B\)。
若存在一种办法使得所有点集 \(A, b\) 的点两两匹配，则称二分图 \(G\) 存在完美匹配。

二分图 \(G\) 存在完美匹配的必要条件是 \(|A| = |B|\)。

一个二分图 \(G\) 存在完美匹配，当且仅当 \(A\) 的任意子集 \(S\), \(B\) 中至少有 \(|S|\) 个不同的点与 \(S\) 相邻。

树

树有很好的性质

任意两点间存在唯一的路径，不存在回路。
树一定存在叶结点，即 \(deg = 1\) 的结点。

树的遍历
前序、中序、后序

直径和重心

求直径

int DFS(int u, int from)
{
	int Max = 0, Maxx = 0;
	for ( int i = 0; i < Edge[u].size(); ++ i )
	{
		int v = Edge[u][i];
		if ( v == from ) continue ;
		int dis = DFS(v, u);
		if ( dis > Max ) { Maxx = Max; Max = dis; }
		else if ( dis > Maxx ) Maxx = dis;
	}
	ans = max(ans, Max + Maxx + 1);
	return Max + 1;
}

求重心

int ans = n + 1, pos = 0;
int DFS(int u, int from) {
	int size = 1, Max = 0;
	for (int i = 0; i < Edge[u].size(); ++ i ) {
		int v = Edge[u][i];
		if ( v == from ) continue ;
		int x = DFS(v, u);
		size += x;
		Max = max(Max, x); 
	}
	Max = max(Max, n - size);
	if ( Max < ans ) {
		ans = Max, pos = u;
	}
	return size;
}