2023五一外出学习整理
Day1:
上午:
引入:

对任意两个元素a,b之间关系(a,b)的取值仅为 True 或者 False,可以考虑使用图来抽象。这样我们称一个元素 a 为一个结点,(a,b)== True 则称结点 a,b 间有连边,否则 a,b 间没有连边。
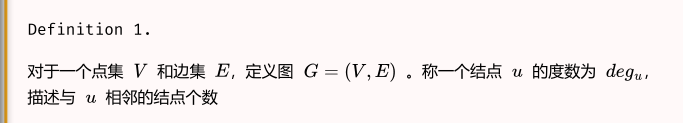
问题转化:一张奇数个点的图 G,证明存在一个点度数为偶数。
转化为更强的问题为:给定一张奇数个点的图 G,证明度数为偶数的点的个数为奇数。
(相反的问题:给定一张奇数个点的图 G,证明度数为奇数的结点的个数为偶数。)
证明:考虑所有点的度数和,由于一条边会被计算到两个结点的度数上,故其必定为偶数。(小学数学易得结论?)


Ex.1:首先可证 n-1 个点与除它之外 n-2 个点连边所以可连 (n-1)(n-2)/2 条边,因此可得 n 个点和至少 ((n-1)(n-2)/2)+1 条边的图是连通图。
Ex.2:
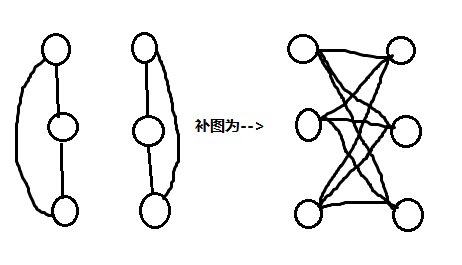
由图可得,对于任意一个图,可将其分为若干个连通块,连通块内部各点都相连,因此其补图原来的连通块内各点于其他各连通块各点相连,因此一定是联通的。
Ex.3:
任意两边至少有一个点是重合的,即为如图:
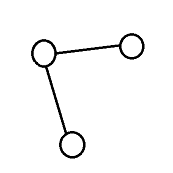
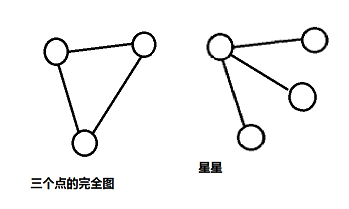
因此当为完全图时,每点度数>=2,因此不可能为星星,反之亦然。
Ex.4:***
Ex.5:分类讨论,
当存在度数为一的点时,删掉度数为一的点剩下的图依旧是连通图。
当不存在时,选择任意一点为起点,计算其他点与起点的距离,删掉距离起点最远的点后,图依旧为连通图。
欧拉回路和哈密顿回路:

1)考虑一个度数为奇数的点,因为它的所有邻边均要遍历恰好一次,故其必须为欧
拉路径的起点或终点。因此可以立即推出,一张存在欧拉路径的图恰好有两个度数为奇数
的点,存在欧拉回路的图没有度数为奇数的点。
2)任意两个回路,可以拼成一个大的回路。
由这两个观察可以发现,Fact 1是存在欧拉路径或者欧拉回路的充要条件。

反证法,假设没有哈密顿回路。
我们由图 G 构造出一个新的没有哈密顿回路的图 G',具体的,令 G'=G,对于每条不在图 G 中的边,如果加入 G' 后不会产生哈密顿回路,则加入,该构造的顺序不重要。
此时我们得到了一个图 G',再加入任何一条边都会得到一条哈密顿回路,并且由于我们仅加入了新的边,所有结点的度数任然大于等于 n/2。
假设 (v1,vn) 这条边不在 G' 中,我们知道必定存在一条哈密顿路径 v1,v2,...,vn 考虑 (v1,vi) 有一条边,则 (vi-1,vn) 必定不能有边,否则可以构造出一条哈密顿回路。
因为这样的 vi 至少有 n/2 个,从而这样的 vi-1 也至少有 n/2 个,又由于 vn 不能和自己连边,故而它至多与 n-n/2-1 个点连边,<=n/2 ,因此与定理矛盾,因此假设不成立。

Ex.6:因为两数互质,因此间隔至少为2,又因为有 n+1,个小于等于 2n 的正整数,所以显然,存在两个数互质。
Ex.7:...
Ex.8:将棋盘进行黑白染色和蓝红染色
Ex.9:Luogu P1341

1 //By:Komorebi_03 2 #include<bits/stdc++.h> 3 using namespace std; 4 #define clear(a) memset(a,0,sizeof a) 5 #define ll long long 6 const int N = 1e3+5; 7 int n,sum,dis[N][N]; 8 char in[N],a[N]; 9 inline int read() 10 { 11 int x=0,f=1;char ch=getchar(); 12 while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();} 13 while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();} 14 return x*f; 15 } 16 17 void Find(int i) 18 { 19 for (int j=1;j<=150;j++) 20 { 21 if(dis[i][j]>0) 22 { 23 dis[i][j]--; 24 dis[j][i]--; 25 Find(j); 26 } 27 } 28 a[++sum]=i; 29 return ; 30 } 31 32 int main() 33 { 34 n=read(); 35 for (int i=1;i<=n;i++) 36 { 37 string s; 38 cin>>s; 39 dis[s[0]][s[1]]++; 40 dis[s[1]][s[0]]++; 41 in[s[0]]++; 42 in[s[1]]++; 43 } 44 int h=0; 45 int cnt=0; 46 for (int i=1;i<=150;i++) 47 { 48 if(in[i] & 1) 49 { 50 cnt++; 51 if(!h) 52 h=i; 53 } 54 } 55 if(!h) 56 { 57 for (int i=0;i<150;i++) 58 { 59 if(in[i]) 60 { 61 h=i; 62 break; 63 } 64 } 65 } 66 if(cnt && cnt!=2) 67 { 68 cout<<"No Solution"; 69 exit(0); 70 } 71 Find(h); 72 if(sum<n+1) 73 { 74 cout<<"No Solution"; 75 exit(0); 76 } 77 for(int i=sum;i>=1;i--) 78 cout<<a[i]; 79 return 0; 80 //Amireux_35 81 }
图的储存和遍历:
1)邻接矩阵: .........没啥可说的
2)邻接表:
vector :

1 #include <vector> 2 vector<int> Edge[1000]; 3 // Edge[i] 是一个一维数组,存了所有 i 能到的点 4 void add(int u, int v) // 插入一条 (u,v) 的边 5 { 6 Edge[u].push_back(v); 7 Edge[v].push_back(u); 8 } 9 void search(int u) // 遍历 u 的所有邻边 10 { 11 for ( int i = 0; i < Edge[u].size(); i++ ) 12 //Edge[u].size() 是unsigned int,0-1=2^32-1 13 { 14 int v = Edge[u][i]; 15 //(u,v) 有一条边 16 ...... 17 } 18 }
链式前向星:

1 int Begin[1000], Next[1000], To[1000], e; 2 void add(int u, int v) // 插入一条 (u,v) 的边 3 { 4 To[++ e] = v; 5 Next[e] = Begin[u]; 6 Begin[u] = e; 7 } 8 void search(int u) 9 { 10 for ( int i = Begin[u]; i; i = Next[i] ) // 遍历 u 的所有邻边 11 { 12 int v = To[i]; 13 ... 14 } 15 }
注:这是ljf的代码,本人等习惯用结构体。
Ex.10:CF 1472C

1 //By:Komorebi_03 2 #include<bits/stdc++.h> 3 using namespace std; 4 #define ll long long 5 const int N = 1e6+5; 6 int T,n,a[N]; 7 bool vis[N]; 8 vector<int> edge[N]; 9 inline int read() 10 { 11 int x=0,f=1;char ch=getchar(); 12 while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();} 13 while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();} 14 return x*f; 15 } 16 17 int dfs(int u) 18 { 19 if(u>n || vis[u]) 20 return 0; 21 vis[u]=true; 22 if(edge[u].size()==1) 23 return a[u]+dfs(edge[u][0]); 24 return a[u]; 25 } 26 27 int main() 28 { 29 T=read(); 30 while (T--) 31 { 32 int ans=0; 33 n=read(); 34 for (int i=1;i<=n;i++) 35 { 36 vis[i]=false; 37 edge[i].clear(); 38 } 39 for (int i=1;i<=n;i++) 40 { 41 cin>>a[i]; 42 edge[i].push_back(i+a[i]); 43 } 44 for (int i=1;i<=n;i++) 45 ans=max(ans,dfs(i)); 46 cout<<ans<<"\n"; 47 } 48 return 0; 49 //Amireux_35 50 }
二分图:

显然,二分图 G 存在完美匹配的必要条件是 ιAι = ιBι


匈牙利算法
Ex.11:Luogu P3386

1 //By:Komorebi_03 2 #include<bits/stdc++.h> 3 using namespace std; 4 #define ll long long 5 const int N = 1e6+5; 6 int n,m,p,ans,cnt,e_cnt,sum[N],dfn[N],head[N]; 7 struct node{ 8 int v; 9 int nxt; 10 }e[N]; 11 inline int read() 12 { 13 int x=0,f=1;char ch=getchar(); 14 while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();} 15 while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();} 16 return x*f; 17 } 18 19 void add(int u,int v) 20 { 21 e[++e_cnt].v=v; 22 e[e_cnt].nxt=head[u]; 23 head[u]=e_cnt; 24 } 25 26 bool dfs(int u,int t) 27 { 28 for (int i=head[u];i;i=e[i].nxt) 29 { 30 int v=e[i].v; 31 if(dfn[v]!=t) 32 { 33 dfn[v]=t; 34 if(!sum[v] || dfs(sum[v],t)) 35 { 36 sum[v]=u; 37 return true; 38 } 39 } 40 } 41 return false; 42 } 43 44 int main() 45 { 46 n=read(); 47 m=read(); 48 p=read(); 49 for (int i=1;i<=p;i++) 50 { 51 int u=read(); 52 int v=read(); 53 if(u>n || v>m) 54 continue; 55 add(u,v); 56 } 57 for (int i=1;i<=n;i++) 58 if(dfs(i,++cnt)) 59 ans++; 60 cout<<ans; 61 return 0; 62 }
Ex.12:CF 1764C

1 //By:Komorebi_03 2 #include<bits/stdc++.h> 3 using namespace std; 4 #define clear(a) memset(a,0,sizeof a) 5 #define int long long 6 const int N = 1e6+5; 7 int T,n,a[N],sum[N]; 8 inline int read() 9 { 10 int x=0,f=1;char ch=getchar(); 11 while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();} 12 while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();} 13 return x*f; 14 } 15 16 signed main() 17 { 18 T=read(); 19 while (T--) 20 { 21 int cnt=0; 22 int ans=0; 23 n=read(); 24 for (int i=1;i<=n;i++) 25 { 26 a[i]=read(); 27 sum[a[i]]++; 28 } 29 sort(a+1,a+1+n); 30 for (int x=1;x<=n;x++) 31 { 32 if(a[x]==a[x-1]) 33 continue; 34 cnt+=sum[a[x]]; 35 if(cnt==n) 36 ans=max(ans,n/2); 37 else 38 ans=max(ans,cnt*(n-cnt)); 39 } 40 cout<<ans<<"\n"; 41 for (int i=1;i<=n;i++) 42 sum[a[i]]--; 43 // memset(sum,0,sizeof sum); 44 } 45 return 0; 46 //Amireux_35 47 }
一份 vector 的使用说明:

1 #include <vector> // 头文件 2 vector<int> a; // 等价于定义一个 int a[] 的数组 3 int a[100]; 4 vector<int> a(100); 5 printf("%d\n", a.size()); // 100 6 a.push_back(1); 7 printf("%d\n", a.size()); // 101 8 a.push_back(x); // 在 a 的最末尾插入一个值为 x 的元素 9 a[i] // 访问 a 的第 i 个元素 10 a.size() // 返回 a 的元素个数(类型为 unsigned int) 11 a.pop() // 移除 a 的最末尾的元素 12 a.empty() // 返回 a 的 size 是否非零 (True or False) 13 a.resize(10) // 修改 a 的 size 为 10
下午:(树)
基本知识:

直观上来说,树等价于没有环的连通图。
树有非常好的性质:
1)任意两点间存在唯一的路径,不存在回路。
2)树一定存在叶结点,即 deg==1 的结点。
树作为一种特殊的图,研究他的重要意义是,在这些特殊性质下,我们可以解决一些在图中无法解决的问题。------ljf
树的储存通常使用与图相同的储存方式,而遍历通常使用DFS

1 DFS(root, 0); // root 表示整棵树的根 2 3 void DFS(int u, int from) 4 { 5 ...... 6 for ( int i = 0; i < Edge[u].size(); ++i ) 7 { 8 int v = Edge[u][i]; 9 if ( v == from ) 10 continue ; 11 DFS(v, u); 12 } 13 ...... 14 }
Ex.1:CF 522A

1 //By:Komorebi_03 2 #include<bits/stdc++.h> 3 using namespace std; 4 #define clear(a) memset(a,0,sizeof a) 5 #define ll long long 6 const int N = 401; 7 int n,cnt,ans,dep[N]; 8 string a,b; 9 map<string,int> mp; 10 vector<vector<int>> g; 11 inline int read() 12 { 13 int x=0,f=1;char ch=getchar(); 14 while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();} 15 while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();} 16 return x*f; 17 } 18 19 void change(string &a) 20 { 21 int len=a.size(); 22 for (int i=0;i<len;i++) 23 { 24 if(a[i]>='A' && a[i]<='Z') 25 { 26 a[i]-='A'; 27 a[i]+='a'; 28 } 29 } 30 } 31 32 void dfs(int x) 33 { 34 for (int i=0;i<g[x].size();i++) 35 { 36 int v=g[x][i]; 37 dep[v]=dep[x]+1; 38 dfs(v); 39 } 40 ans=max(ans,dep[x]); 41 } 42 43 int main() 44 { 45 n=read(); 46 g.resize(2*n+3); 47 for (int i=1;i<=n;i++) 48 { 49 cin>>a>>b>>b; 50 change(a); 51 change(b); 52 if(!mp.count(a)) 53 mp[a]=++cnt; 54 if(!mp.count(b)) 55 mp[b]=++cnt; 56 g[mp[a]].push_back(mp[b]); 57 } 58 for (int i=1;i<=cnt;i++) 59 { 60 if(!dep[i]) 61 { 62 dep[i]=1; 63 dfs(i); 64 } 65 } 66 cout<<ans; 67 return 0; 68 //Amireux_35 69 }
Ex.2:CF 115A

1 //By:Komorebi_03 2 #include<bits/stdc++.h> 3 using namespace std; 4 #define clear(a) memset(a,0,sizeof a) 5 #define ll long long 6 const int N = 1e6+5; 7 int n,ans,fa[N]; 8 inline int read() 9 { 10 int x=0,f=1;char ch=getchar(); 11 while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();} 12 while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();} 13 return x*f; 14 } 15 16 int Find(int x) 17 { 18 int cnt=0; 19 while (x!=-1) 20 { 21 x=fa[x]; 22 cnt++; 23 } 24 return cnt; 25 } 26 27 int main() 28 { 29 n=read(); 30 for (int i=1;i<=n;i++) 31 fa[i]=read(); 32 for (int i=1;i<=n;i++) 33 ans=max(ans,Find(i)); 34 cout<<ans; 35 return 0; 36 //Amireux_35 37 }
直径和重心:
称树的直径为树上最长的一条路径,树的重心为 删去这个点后,最大的子树最小

1 int DFS(int u, int from) 2 { 3 int Max = 0, Maxx = 0; 4 for ( int i = 0; i < Edge[u].size(); ++ i ) 5 { 6 int v = Edge[u][i]; 7 if ( v == from ) continue ; 8 int dis = DFS(v, u); 9 if ( dis > Max ) { Maxx = Max; Max = dis; } 10 else if ( dis > Maxx ) Maxx = dis; 11 } 12 ans = max(ans, Max + Maxx + 1); 13 return Max + 1; 14 }

1 int ans = n + 1, pos = 0; 2 int DFS(int u, int from) 3 { 4 int size = 1, Max = 0; 5 for ( int i = 0; i < Edge[u].size(); ++ i ) 6 { 7 int v = Edge[u][i]; 8 if ( v == from ) continue ; 9 int x = DFS(v, u); 10 size += x; 11 Max = max(Max, x); 12 } 13 Max = max(Max, n - size); 14 if ( Max < ans ) { ans = Max, pos = u; } 15 return size; 16 }
Ex.3:CF 690C2

1 //By:Komorebi_03 2 #include<bits/stdc++.h> 3 using namespace std; 4 #define clear(a) memset(a,0,sizeof a) 5 #define ll long long 6 const int N = 1e6+5; 7 int n,m,p,ans,e_cnt,dis[N],head[N]; 8 struct node{ 9 int v; 10 int nxt; 11 }e[N]; 12 inline int read() 13 { 14 int x=0,f=1;char ch=getchar(); 15 while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();} 16 while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();} 17 return x*f; 18 } 19 20 void add(int u,int v) 21 { 22 e[++e_cnt].v=v; 23 e[e_cnt].nxt=head[u]; 24 head[u]=e_cnt; 25 } 26 27 void dfs(int u,int frm) 28 { 29 int Max=0; 30 int Maxx=0; 31 for (int i=head[u];i;i=e[i].nxt) 32 { 33 int v=e[i].v; 34 if(v==frm) 35 continue; 36 dfs(v,u); 37 int w = dis[v]+1; 38 dis[u]=max(dis[u],w); 39 if(w>Max) 40 { 41 Maxx=Max; 42 Max=w; 43 } 44 else if (w>Maxx) 45 Maxx=w; 46 } 47 ans=max(ans,Max+Maxx); 48 } 49 50 int main() 51 { 52 n=read(); 53 m=read(); 54 for (int i=1;i<=m;i++) 55 { 56 int u=read(); 57 int v=read(); 58 add(u,v); 59 add(v,u); 60 } 61 dfs(1,0); 62 cout<<ans; 63 return 0; 64 }
最近公共祖先:

倍增算法


1 int LCA(int u, int v) 2 { 3 if ( dis[u] < dis[v] ) swap(u,v); 4 for ( int j = 20; j >= 0; -- j ) 5 if ( dis[f[u][j]] >= dis[v] ) u = f[u][j]; 6 if ( u == v ) return u; 7 for ( int j = 20; j >= 0; -- j ) 8 if ( f[u][j] != f[v][j] ) { u = f[u][j]; v = f[v][j]; } 9 return f[u][0]; 10 } 11 void INIT() 12 { 13 DFS(); // 使用 DFS 处理好 f[u][0] 和 dis[u] 14 for ( int j = 1; j <= 20; ++ j ) 15 for ( int i = 1; i <= n; ++ i ) 16 f[i][j] = f[f[i][j - 1]][j - 1]; 17 }
Tarjan算法

1 void DFS(int u, int from) 2 { 3 vis[u] = true; 4 for ( int i = 0; i < Edge[u].size(); ++ i ) 5 { 6 int v = Edge[u][i]; 7 if ( v == from ) continue ; 8 DFS(v, u); 9 Merge(u, v); // 并查集 10 } 11 for ( int i = 0; i < query[u].size(); ++ i ) // 在 u 点的查询列表 12 { 13 int v = query[u][i]; 14 if ( vis[v] == true ) ans[u][v] = Find(v); 15 //u,v 的查询答案是Find(v) 16 } 17 }
其它:
满二叉树是一种特殊的树,所有非叶结点都恰有两个子结点,它拥有更加优秀的性质:

Ex.4:CF 1741D

1 //By:Komorebi_03 2 #include<bits/stdc++.h> 3 using namespace std; 4 #define clear(a) memset(a,0,sizeof a) 5 #define ll long long 6 const int N = 1e6+5; 7 int T,n,a[N]; 8 inline int read() 9 { 10 int x=0,f=1;char ch=getchar(); 11 while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();} 12 while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();} 13 return x*f; 14 } 15 16 int main() 17 { 18 T=read(); 19 while (T--) 20 { 21 n=read(); 22 clear(a); 23 for (int i=1;i<=n;i++) 24 a[i]=read(); 25 int cnt=0; 26 bool flag=false; 27 for (int i=2;i<=n;i<<=1) 28 { 29 for (int j=i;j<=n;j+=i) 30 { 31 if(a[j-(i>>1)]>a[j]) 32 { 33 swap(a[j-(i>>1)],a[j]); 34 cnt++; 35 } 36 if(a[j-(i>>1)]+(i>>1)!=a[j]) 37 { 38 cout<<-1<<"\n"; 39 flag=true; 40 break; 41 } 42 } 43 if(flag) 44 break; 45 } 46 if(flag) 47 continue; 48 cout<<cnt<<"\n"; 49 } 50 return 0; 51 //Amireux_35 52 } 53 54 /* 55 你考虑根左子树的数集合是A 56 右子树的数集合是B 57 那么无论你左右子树内部怎么转 58 这个集合是不会变的 59 所以你只有可能通过根的交换 60 来换A,B这两个完整的集合 61 所以有解当且仅当 62 A,B集合有一个全是小的数 63 另外一个全是大的数 64 然后递归做这个问题就行 65 */
Ex.5:CF 1675D

1 // Problem: CF1675D Vertical Paths 2 // Contest: Luogu 3 // URL: https://www.luogu.com.cn/problem/CF1675D 4 // Memory Limit: 250 MB 5 // Time Limit: 2000 ms 6 // 7 // Powered by CP Editor (https://cpeditor.org) 8 9 //By:Komorebi_03 10 #include<bits/stdc++.h> 11 using namespace std; 12 #define clear(a) memset(a,0,sizeof a) 13 #define ll long long 14 const int N = 2e6+5; 15 int T,n,ans,y[N],p[N],sum[N]; 16 bool vis[N]; 17 inline int read() 18 { 19 int x=0,f=1;char ch=getchar(); 20 while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();} 21 while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();} 22 return x*f; 23 } 24 25 int main() 26 { 27 T=read(); 28 while (T--) 29 { 30 ans=0; 31 n=read(); 32 for (int i=1;i<=n;i++) 33 { 34 vis[i]=false; 35 y[i]=1; 36 } 37 for (int i=1;i<=n;i++) 38 { 39 p[i]=read(); 40 if(p[i]!=i) 41 y[p[i]]=0; 42 } 43 for (int i=1;i<=n;i++) 44 if(y[i]) 45 ans++; 46 cout<<ans<<"\n"; 47 for (int i=1;i<=n;i++) 48 { 49 if(y[i]) 50 { 51 int now=i; 52 int cnt=0; 53 while (!vis[now]) 54 { 55 sum[++cnt]=now; 56 vis[now]=true; 57 if(p[now]==now) 58 break; 59 now=p[now]; 60 } 61 cout<<cnt<<"\n"; 62 for (int j=cnt;j>=1;j--) 63 cout<<sum[j]<<" "; 64 putchar('\n'); 65 } 66 } 67 putchar('\n'); 68 } 69 return 0; 70 //Amireux_35 71 }
Day2:
上午:
生成树问题:
DFS生成树:
对于任意一棵DFS生成树,其必定只有返祖边,没有横叉边,在求割点和强连通分量上方便很多。
CF 1104E
CF 1726D
最小生成树:
1)Kruskal
贪心的思想,最小生成树肯定会尽可能的包含边权较小的边
考虑将将所有边权按从小到大排序,依次判断,若没有与之前选择的边一起构成环,则选择该边
正确性可以考虑对于边 e,若加入它后就不能变成最优的生成树 T,则 T+e 必定构成环
Luogu P3366

1 //By:Komorebi_03 2 #include<bits/stdc++.h> 3 using namespace std; 4 #define clear(a) memset(a,0,sizeof a) 5 #define ll long long 6 const int N = 1e6+5; 7 int n,m,cnt,ans,e_cnt,fa[N]; 8 bool flag; 9 struct node{ 10 int u; 11 int v; 12 int w; 13 }e[N]; 14 inline int read() 15 { 16 int x=0,f=1;char ch=getchar(); 17 while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();} 18 while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();} 19 return x*f; 20 } 21 22 void add(int u,int v,int w) 23 { 24 e[++e_cnt].u=u; 25 e[e_cnt].v=v; 26 e[e_cnt].w=w; 27 } 28 29 int Find(int x) 30 { 31 if(x==fa[x]) 32 return x; 33 return fa[x]=Find(fa[x]); 34 } 35 36 bool cmp(node a,node b) 37 { 38 return a.w<b.w; 39 } 40 41 int main() 42 { 43 n=read(); 44 m=read(); 45 for (int i=1;i<=m;i++) 46 { 47 int x=read(); 48 int y=read(); 49 int w=read(); 50 add(x,y,w); 51 } 52 for (int i=1;i<=n;i++) 53 fa[i]=i; 54 sort(e+1,e+1+e_cnt,cmp); 55 for (int i=1;i<=e_cnt;i++) 56 { 57 int u=e[i].u; 58 int v=e[i].v; 59 int w=e[i].w; 60 int r1=Find(u); 61 int r2=Find(v); 62 if(r1!=r2) 63 { 64 fa[r2]=r1; 65 cnt++; 66 ans+=w; 67 } 68 if(cnt==n-1) 69 { 70 flag=true; 71 break; 72 } 73 } 74 if(flag) 75 cout<<ans; 76 else 77 puts("orz"); 78 return 0; 79 //Amireux_35 80 }
2)Prim
同样使用贪心的思想,Kruskal是加边,Prim是加点构成最小生成树
具体的,从任意结点开始,每次选择一个距离当前已选结点最近的点,选择并重复

最小生成树 - OI Wiki (oi-wiki.org)(严格次小/非严格次小生成树)
CF 707B
就是对于每一个仓库考虑与它有连边的非仓库的最短距离。
(为什么这么做是对的,因为除了仓库,所有点都是非仓库,那么如果最后选的点和最靠近它的仓库不是相邻的,那么必然可以在这个点与最靠近它的仓库的路径上选一个点使得答案可以更小)
然后把所有的取一个最小值,若所有仓库旁边都没有非仓库,那么输出 −1。

1 //By:Komorebi_03 2 #include<bits/stdc++.h> 3 using namespace std; 4 #define clear(a) memset(a,0,sizeof a) 5 #define ll long long 6 const int INF = 0x3f3f3f3f; 7 const int N = 1e6+5; 8 int n,m,k,e_cnt,head[N]; 9 bool vis[N]; 10 struct node{ 11 int v; 12 int w; 13 int nxt; 14 }e[N]; 15 inline int read() 16 { 17 int x=0,f=1;char ch=getchar(); 18 while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();} 19 while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();} 20 return x*f; 21 } 22 23 void add(int u,int v,int w) 24 { 25 e[++e_cnt].v=v; 26 e[e_cnt].w=w; 27 e[e_cnt].nxt=head[u]; 28 head[u]=e_cnt; 29 } 30 31 int main() 32 { 33 n=read(); 34 m=read(); 35 k=read(); 36 for (int i=1;i<=m;i++) 37 { 38 int u=read(); 39 int v=read(); 40 int w=read(); 41 add(u,v,w); 42 add(v,u,w); 43 } 44 for (int i=1;i<=k;i++) 45 vis[read()]=true; 46 int ans=INF; 47 for (int i=1;i<=n;i++) 48 if(vis[i]) 49 for (int j=head[i];j;j=e[j].nxt) 50 if(!vis[e[j].v]) 51 ans=min(ans,e[j].w); 52 if(ans==INF) 53 cout<<-1; 54 else 55 cout<<ans; 56 return 0; 57 //Amireux_35 58 }
CF 1242B
CF 606D
下午:
最短路问题:
1)Floyd

Floyd还有很多用处
比如:找图中最小环,任意两点最短路径数,计算一个图的传递背包(判断两点是否联通)
2)Dijkstra
单元最短路径算法,即求起点 S 到所有点的最短距离,但有一个限制是不能存在负权边

3)SPFA
用于负权边的图求最短路径

CF 95C
次短路问题:

CF 25C
CF 938D
差分约束:

CF 1450E
CF 1131D
CF 1473E
CF 208C
扩展
prufer序列
对于这样一棵树:
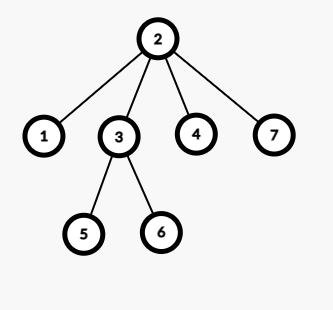
初始叶结点最小为 1 号,因此对应的prufer序列先是 2
然后叶结点 4 号对应的prufer序列是 2
依次可得 5 号对应 3,6 号对应 3,3 号对应 2,7 号对应 2;
最后这棵树的prufer序列为 223322
Prüfer 序列 - OI Wiki (oi-wiki.org)
day3:
连通性问题:
有向无环图:
有向无环图是一种特殊的图,其最大意义在于能够拓扑排序。

拓扑排序:
考虑维护一个入度为 0 的点的集合
因为这些点之间没有依赖关系,我们可以将它放在序列的开头,所有依赖关系,我们可以将它放在序列的开头,所有依赖它的点都在它后面
放在开头后删掉它,更新剩余入度为 0 的点,继续这个过程
CF 1572A
CF 510C
CF 1679D
强连通分量:


CF 1220E
CF 118E
有桥则一定无解
无桥则一定有解
注意路径输出

1 //By:Komorebi_03 2 #include<bits/stdc++.h> 3 using namespace std; 4 #define clear(a) memset(a,0,sizeof a) 5 #define ll long long 6 const int N = 1e6+5; 7 int n,m,tim,cnt,e_cnt,dfn[N],low[N],head[N]; 8 bool vis[N]; 9 struct node{ 10 int v; 11 int nxt; 12 }e[N]; 13 struct edge{ 14 int u; 15 int v; 16 }; 17 int ansu[N],ansv[N]; 18 inline int read() 19 { 20 int x=0,f=1;char ch=getchar(); 21 while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();} 22 while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();} 23 return x*f; 24 } 25 26 void add(int u,int v) 27 { 28 e[++e_cnt].v=v; 29 e[e_cnt].nxt=head[u]; 30 head[u]=e_cnt; 31 } 32 33 void TJ(int u,int fa) 34 { 35 low[u]=dfn[u]=++tim; 36 vis[u]=true; 37 for (int i=head[u];i;i=e[i].nxt) 38 { 39 int v=e[i].v; 40 if(v==fa) 41 continue; 42 if(!dfn[v]) 43 { 44 TJ(v,u); 45 ansu[++cnt]=u; 46 ansv[cnt]=v; 47 low[u]=min(low[u],low[v]); 48 } 49 else 50 { 51 low[u]=min(low[u],dfn[v]); 52 if(dfn[v]<dfn[u]) 53 { 54 ansu[++cnt]=u; 55 ansv[cnt]=v; 56 } 57 } 58 if(low[v]>dfn[u]) 59 { 60 putchar('0'); 61 exit(0); 62 } 63 } 64 } 65 66 int main() 67 { 68 n=read(); 69 m=read(); 70 for (int i=1;i<=m;i++) 71 { 72 int u=read(); 73 int v=read(); 74 add(u,v); 75 add(v,u); 76 } 77 TJ(1,-1); 78 for (int i=1;i<=cnt;i++) 79 cout<<ansu[i]<<" "<<ansv[i]<<"\n"; 80 return 0; 81 //Amireux_35 82 }
CF 555E
CF 427C
2-SAT:

CF 1697F
CF 1475F
线段树:
李超线段树
数学:
概率论
导数
同余
day4:
上午:
图论精题:
线性代数
下午:
NOIP历年真题:
P7113 [NOIP2020] 排水系统
题面非常复杂(简直可以说ex,简化为:给出一个DAG,1 ~ m为源点,出度为零的点是汇点,每个源点流量为1,过程中每个节点的流量均等的流向所有的出路。求每个汇点的流量。
依据题意建图:
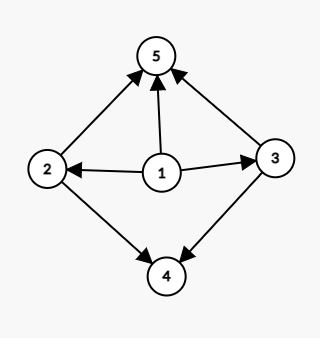
但是这题还需要高精,已经忘记高精怎么写了,所以这里用了__int128(不是懒

1 // Problem: P7113 [NOIP2020] 排水系统 2 // Contest: Luogu 3 // URL: https://www.luogu.com.cn/problem/P7113 4 // Memory Limit: 512 MB 5 // Time Limit: 1000 ms 6 // 7 // Powered by CP Edixr (https://cpedixr.org) 8 9 //By:Komorebi_03 10 #include<bits/stdc++.h> 11 using namespace std; 12 #define clear(a) memset(a,0,sizeof a) 13 #define ll __int128 14 const int N = 1e6+5; 15 int n,m,sum,e_cnt,d[N],in[N],num[N],head[N]; 16 struct edge{ 17 int v; 18 int nxt; 19 }e[N]; 20 struct node{ 21 ll fz; 22 ll fm; 23 }k[N]; 24 queue<int> q; 25 inline int read() 26 { 27 int x=0,f=1;char ch=getchar(); 28 while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();} 29 while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();} 30 return x*f; 31 } 32 33 void write(ll x) 34 { 35 if(x/10) 36 write(x/10); 37 putchar(x%10+'0'); 38 } 39 40 void add(int u,int v) 41 { 42 e[++e_cnt].v=v; 43 e[e_cnt].nxt=head[u]; 44 head[u]=e_cnt; 45 } 46 47 ll gcd(ll x,ll y) 48 { 49 if(y==0) 50 return x; 51 else 52 return gcd(y,x%y); 53 } 54 55 void yf(int p) 56 { 57 ll tmp=gcd(k[p].fz,k[p].fm); 58 k[p].fz/=tmp; 59 k[p].fm/=tmp; 60 } 61 62 void clac(int x,int now) 63 { 64 ll kkk=k[x].fm*k[now].fm/(gcd(k[x].fm,k[now].fm)); 65 k[x].fz=k[x].fz*(kkk/k[x].fm); 66 k[now].fz=k[now].fz*(kkk/k[now].fm); 67 k[x].fz=k[x].fz+k[now].fz; 68 k[x].fm=k[now].fm=kkk; 69 if(k[x].fz) 70 yf(x); 71 } 72 73 void TP() 74 { 75 while (!q.empty()) 76 { 77 int u=q.front(); 78 bool flag=false; 79 q.pop(); 80 if(d[u]) 81 k[u].fm*=d[u]; 82 if(k[u].fz) 83 yf(u); 84 for (int i=head[u];i;i=e[i].nxt) 85 { 86 flag=true; 87 int v=e[i].v; 88 in[v]--; 89 clac(v,u); 90 if(!in[v]) 91 q.push(v); 92 } 93 if(flag) 94 { 95 k[u].fz=0; 96 k[u].fm=1; 97 } 98 } 99 } 100 101 int main() 102 { 103 n=read(); 104 m=read(); 105 for (int i=1;i<=n;i++) 106 { 107 k[i].fz=0; 108 k[i].fm=1; 109 d[i]=read(); 110 if(!d[i]) 111 num[++sum]=i; 112 for (int j=1;j<=d[i];j++) 113 { 114 int a=read(); 115 add(i,a); 116 in[a]++; 117 } 118 } 119 for (int i=1;i<=n;i++) 120 { 121 if(!in[i]) 122 { 123 k[i].fz=k[i].fm=1; 124 q.push(i); 125 } 126 } 127 TP(); 128 for (int i=1;i<=sum;i++) 129 { 130 yf(num[i]); 131 write(k[num[i]].fz); 132 putchar(' '); 133 write(k[num[i]].fm); 134 putchar('\n'); 135 } 136 return 0; 137 //Amireux_35 138 }
P1525 [NOIP2010 提高组] 关押罪犯
P1983 [NOIP2013 普及组] 车站分级
P2296 [NOIP2014 提高组] 寻找道路
P1967 [NOIP2013 提高组] 货车运输
P2661 [NOIP2015 提高组] 信息传递
P2680 [NOIP2015 提高组] 运输计划
