新高一暑假第一期集训恢复性训练【树状数组巩固小练】(补)
新高一暑假第一期集训恢复性训练【树状数组巩固小练】(补)
A. [POJ2182] Lost Cows
不难发现要从后往前确定每头牛的身高,这样每头牛的身高就是 \(1\sim n\) 中没被选过的第 \(a_i + 1\) 大的数(因为有 \(a_i\) 头比自己矮),那么我们只需用树状数组维护一个 \(01\) 序列,没选过的数标为 \(1\),每次查询时二分 \(mid\),通过树状数组 \(\operatorname{sum}(mid)\) 计算前 \(mid\) 个数有几个为 \(1\) 即没被选过的,直到找到 \(a_i+1\)。
B. [POJ1990] MooFest
先将二元组按照 \(v\) 从小到大排序,保证每头牛比前面的牛的 \(v\) 大,计算它和它前面的牛的音量和的时候就可以直接用这头牛的 \(v\),还需要计算出 \(|x_i - x|\) 之和。
树状数组维护 \(x\),可以直接求出比这头牛小的所有 \(x\) 之和,还需要用另一个树状数组维护每个元素出现的次数,直接求出小于这头牛的 \(x\) 的牛的数目。
C. [ARC107D] Median of Medians
二分最后的中位数,然后将原序列中大于 \(mid\) 的标为 \(1\),小于的标为 \(-1\),前缀和。
只要一段区间的和 \(\gt 0\),那么这段区间的中位数就一定大于等于 \(mid\)。
所以问题转化为:求出当前这个序列的顺序对个数。
于是做法显然。用树状数组维护,注意树状数组下标不能有负数,所以加上 \(N\) 强制转正。
时间复杂度 \(\Theta(n\log n\log \max\{a_i\})\)。
D. [ARC101F] Robots and Exits
对于一个机器人,设它到左边出口的距离为 \(a_i\),到右边出口的距离为 \(b_i\),那就可以把它看成一个点 \((a_i, b_i)\)。
设 \(x\) 为所有机器人往左移动的最远点到初始位置的距离,\(y\) 是所有机器人往右移动的最远点到初始位置的距离。
那么每次可以选择把 \((x, y)\) 变成 \((x + 1, y)\) 或者 \((x, y + 1)\)。
当 \(x = a_i\) 时,第 \(i\) 个机器人会从左边的出口出去,当 \(y = b_i\) 时,机器人会从右边的出口出去。
那么可以看成从原点开始走,每次往上或右走一步。最后走的这条折线的上方和下方分别对应着从左边和右边的出口出去的机器人的集合。
那么考虑把折线往下移,变成这样:
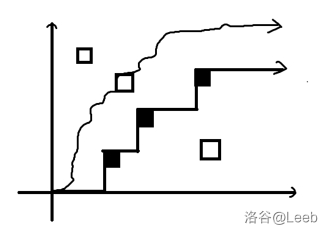
那么一条折线可以用折线经过的点(黑框框)来表示。
设 \(f_i\) 为最后一个经过的黑框框是 \(i\) 的方案数。
则 \(\displaystyle f_i = 1 + \sum\limits_{x_j \lt x_i, y_j \lt y_i} f_j\) ,树状数组维护。
时间复杂度为 \(\Theta(n\log n)\)。