图论优化
图论优化
三元环计数
首先给所有边定向,从度数小的点指向度数大的点,如果度数一样,则从编号小的指向编号大的,最终形成一张DAG。
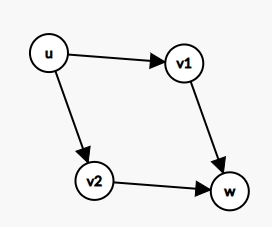
枚举\(u\)以及\(u\)指向的点\(v\)以及\(v\)指向的点\(w\),如果\(u\)也指向\(w\)则成三元环。
如果要一开始是有向图计数则最后判断一下\(u,v,w\)的方向即可。
时间复杂度\(\mathcal O(m\sqrt m)\)。
由于这里相当于遍历了所有的三元环,所以理论上来说可以做出很多神奇的操作。
时间复杂度证明:
设节点\(v\)的入度为\(d(u)\),对于一对 \((v,w)\) 来说。
-
如果 \(d(v)\le \sqrt m\),则因为点 \(w\) 至多有\(n\) 个,所以这里的复杂度为 \(\mathcal O(n\sqrt m)\)。
-
如果 \(d(v)>\sqrt m\),则因为 \(d(v)<d(w)\),所以\(d(w)>\sqrt m\),因为总边数只有 \(m\),所以这里的 \(w\) 至多只有 \(\sqrt m\) 个。总复杂度 \(\mathcal O(m\sqrt m)\)。
所以总复杂度为 \(\mathcal O(m\sqrt m)\)。
四元环计数
首先给所有边定向,从度数小的点指向度数大的点,如果度数一样,则从编号小的指向编号大的,最终形成一张DAG。
枚举点 \(u\)以及\(u\)指向的点 \(v\),以及\(v\)指向的点\(w\),累加上前面使得 \((u,w)\) 右边的 \(v\) 的个数即可。原理图如下: