算法笔记-字符串算法集合（未完）

幽光闪烁 / 2024-11-05 / 原文

这里有一些别样的学习思路。

KMP

用途

单模式串匹配。

过程

我们分解 $O(nm)$ 的算法过程。

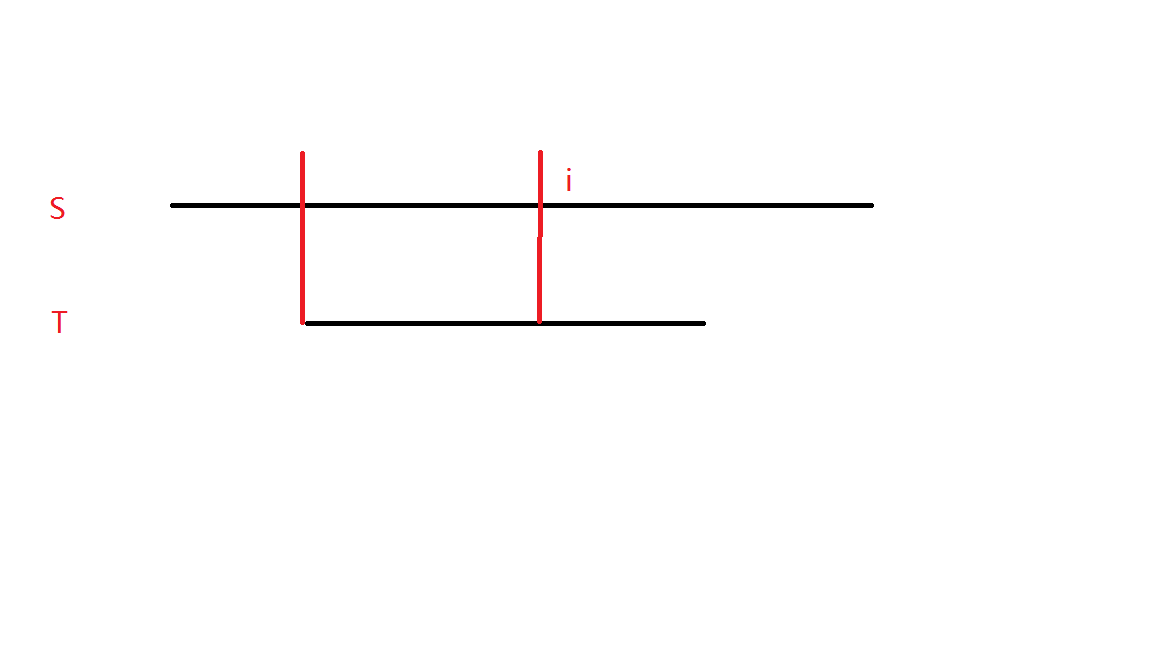
如图，红色竖线包括的为目前匹配成功的部分，对于下一位 $i$ ：

首先，如果成功匹配，那么匹配长度加一。

否则，我们考虑失配情况。

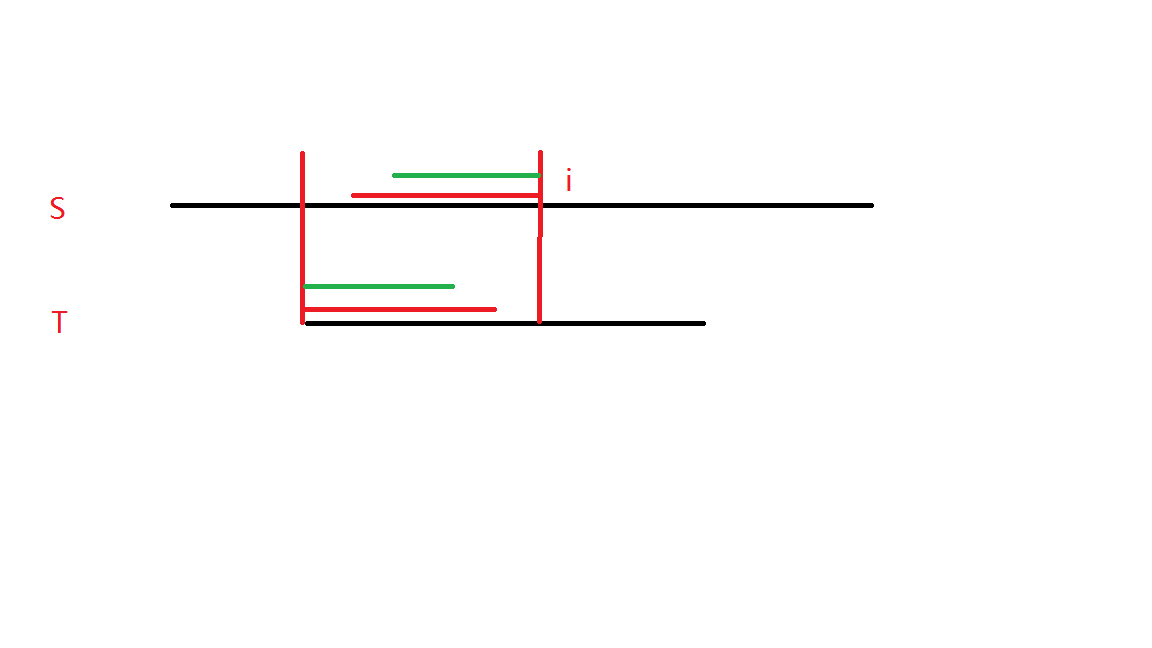
我们会将 $S$ 串的匹配部分左端点向右移动一位，然后 $T$ 串从头匹配。

我们发现，如果想要再次考虑第 $i$ 位，最起码需要匹配到如上图中红色横线的部分，也就是说红色横线的部分完全相等。

如果不完全相等，我们需要比较绿色横线的部分，如此以往。

要么，我们遍历了所有的起点，不存在这种情况，我们就以 $i$ 位为起点开始重复这个过程。
要么，我们找到了另一个起点，使得我们可以重新考虑第 $i$ 位的匹配情况。

我们发现，第二种情况中，我们一定找到了红色竖线内的 最长公共前后缀。

也就是说，当失配时，我们只需要知道，当前已匹配 $T$ 串部分的最长公共前后缀。
如果仍然失配，我们继续找到 $T$ 的最长公共前后缀的最长公共前后缀，重复此过程。

一个字符串 $S$ 的 最长公共前后缀 为 $S$ 的长度最长的真子串 $T$，满足 $T$ 既是 $S$ 的前缀，也是 $S$ 的后缀，以下称作 $\texttt{boarder}$。

由此，我们便建立了较为完整的思维过程来优化此算法。

可以发现，我们尽可能地减少了重复的，或者说无意义的比较，算法的 正确性 由此保证。

$\texttt{boarder}$ 求法

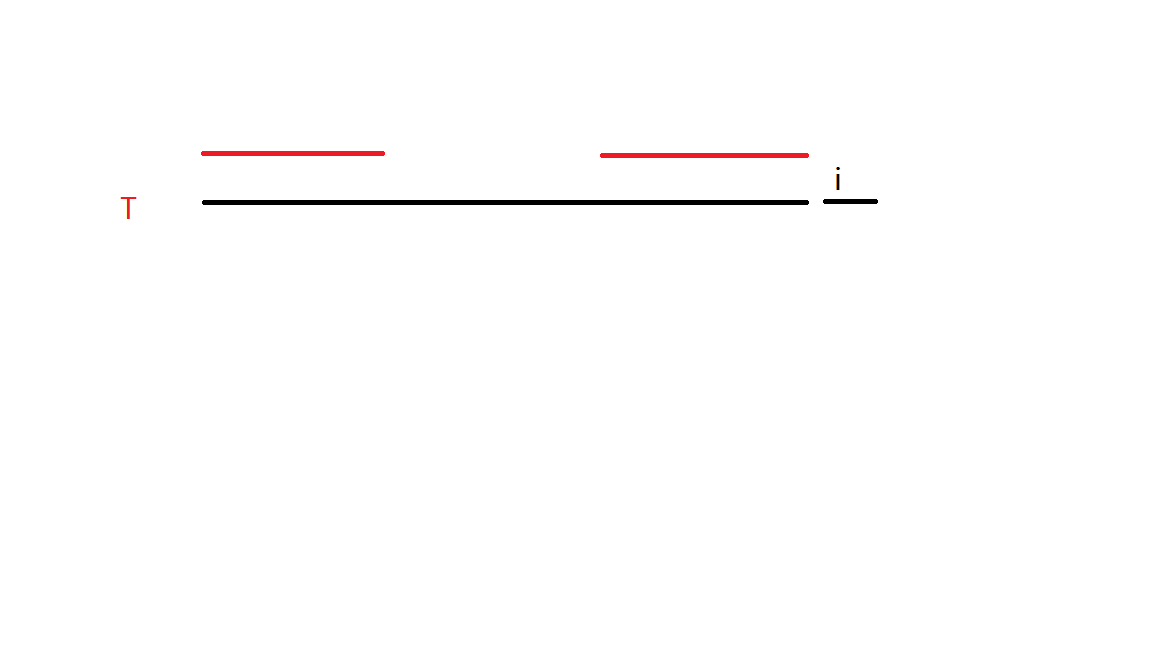
我们用红色横线表示第 $i - 1$ 位的 $\texttt{boarder}$。
可以发现，此过程类似于 $T$ 的自身匹配，与上述优化过程类似。

时间复杂度

首先来看两主要部分代码：

for (int i = 2, j = 0; i <= M; ++i) {
	while (j and t[j + 1] != t[i]) j = p[j];
	if (t[j + 1] == t[i]) ++j;
	p[i] = j;
}
for (int i = 1, j = 0; i <= N; ++i) {
	while (j and s[i] != t[j + 1]) j = p[j];
	if (s[i] == t[j + 1]) ++j;
	if (j == M) ans.push_back(i - M + 1), j = p[j];
}
//Luogu P3375

以 $\texttt{boarder}$ 的处理为例，我们发现，变量 $j$ 最多增量为 $O(n)$，也就最多向前跳 $O(n)$ 次，复杂度为 $O(n)$。
匹配过程同理。

总复杂度 $O(n + m)$。