代码随想录算法训练营第二天 | 209. 长度最小的子数组、 59.螺旋矩阵II
4-209.长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其总和大于等于 target 的长度最小的 子数组[numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。示例 2:
输入:target = 4, nums = [1,4,4]
输出:1示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1]
输出:0提示:
1 <= target <= 1091 <= nums.length <= 1051 <= nums[i] <= 105
进阶:
- 如果你已经实现
O(n)时间复杂度的解法, 请尝试设计一个O(n log(n))时间复杂度的解法。
寻找子数组,最简单的想法就是直接用两层for循环进行暴力求解,两层for循环嵌套,据说会超时所以我就没尝试。
为了设计O(n)时间复杂度的算法,就需要用到滑窗。其实从第一天就想问,时间复杂度是啥,本人不是计算机专业,所以以前涉及到写代码的时候其实并没有考虑这些,能动就行.jpg。于是又去补习了一下时间复杂度的问题。
时间复杂度是计算机科学中用于描述一个算法的运行时间随输入规模变化而变化的指标。它衡量了算法执行所需的时间随着输入大小的变化情况。时间复杂度帮助我们了解算法在输入规模增加时效率的变化趋势,而不必关注具体的硬件或实现的细节。
通常,时间复杂度使用大O符号来表示,它表明了算法在最坏情况下的执行时间增长率。
常见的时间复杂度类型
- O(1):常数时间复杂度,算法的执行时间与输入规模无关,始终是一个常数。例如,直接访问数组中的某个元素。
- O(log n):对数时间复杂度,随着输入规模增加,时间复杂度以对数速度增长。常见于二分查找算法。
- O(n):线性时间复杂度,执行时间与输入规模成正比。例如,遍历一个长度为 nn 的数组时,算法需要执行 nn 次操作。
- O(n log n):常见于高效的排序算法,如归并排序、堆排序。
- O(n^2):二次时间复杂度,执行时间随着输入规模的平方增长,常见于简单的嵌套循环(如冒泡排序、选择排序)。
- O(2^n):指数时间复杂度,执行时间随着输入规模的指数增长,常见于递归算法(如解决“汉诺塔”问题的递归算法)。
- O(n!):阶乘时间复杂度,常见于暴力求解排列组合问题的算法。
卡哥的视频讲解比文字版好理解一些,但还是要自己琢磨一下才能想明白,其实滑窗本质上和双指针思路一样,j指针负责向后移动,在移动到某位置时,此时前面所有数的和大于目标值,首先记录此时的子数组长度,然后判断是否需要更新result,最后开始尝试移动i指针,此时只要依然大于目标值,就继续记录。
这里文字说明非常无力,我画个图来演示
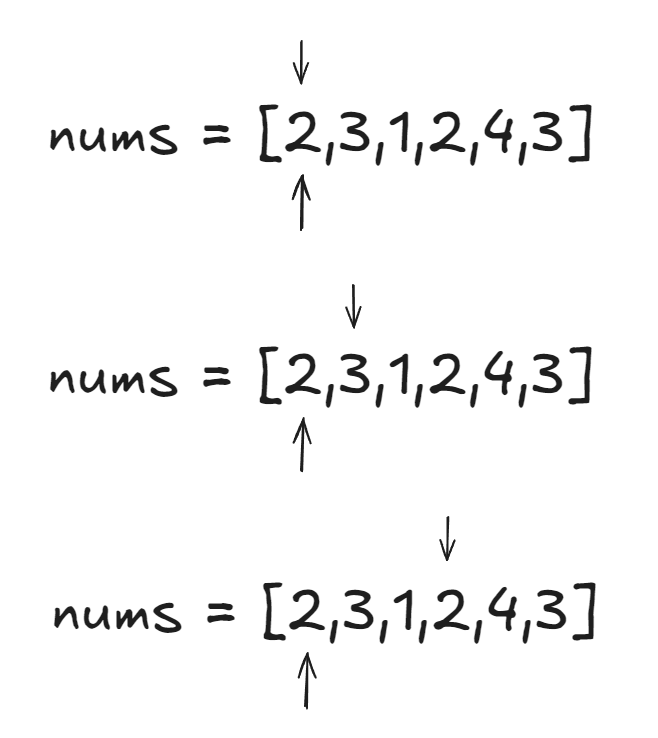
如上图所示,我们的j就是上面的指针,随着它的移动,前面所有项加和会逐渐增加,这里我们设定目标值为7,那么在第三张图时其实已经达到8了,记录最小值为4,也就是2312这四个数,此时下面的指针会移动,来尝试缩小数组,于是如图。
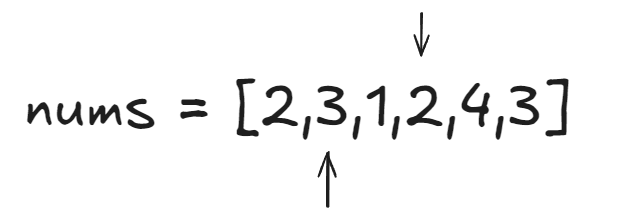
此时sum的和就只有6了,不满足我们的条件,于是不更新最小数组值而是将j指针继续移动。每次都会逐渐缩短数组,于是最后就可以得出2的结果,也就是43的部分,就像一个贪吃蛇在逐渐伸缩身体去寻找最小长度覆盖到指定数值。代码如下:
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int sum = 0;//和
int i =0;//后指针
int subL = 0;//目前子集长度
int result = INT32_MAX;//将结果定义为最大值
for(int j = 0;j < nums.size(); j++){
sum += nums[j];
while(sum >= target){
subL = (j - i + 1);
result = result < subL ? result : subL;//判断result和subl中的最小值,进行赋值
sum-=nums[i++];//c++特化写法,省去一行半。
}
}
return result == INT32_MAX ? 0 : result;//如果没成功找到任何一个,那么返回一个0
}
};5-59.螺旋矩阵II
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例 1:

输入:n = 3
输出:[[1,2,3],[8,9,4],[7,6,5]]示例 2:
输入:n = 1
输出:[[1]]
提示:
1 <= n <= 20
螺旋矩阵问题的关键就在于打印每条边的时候的规则,只要能够统一打印规则,那么问题就会简单很多。采用每条边打印第一个点,不打印最后一个点的原则进行编写。代码如下:
class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
vector<vector<int>> res(n, vector<int>(n,(n*n)));//直接将矩阵赋值为n*n来规避奇数矩阵导致的最后一个数的问题
int startx = 0, starty = 0;//定义开始点
int offset = 1;
int count = 1;
int loop = n/2;
while(loop--){
int i = startx;
int j = starty;
for(j = starty; j < n - offset; j++){//打印第一条边
res[startx][j] = count++;
}
for(i = startx; i < n - offset; i++){//打印第二条边
res[i][j] = count++;
}
for(;j > starty; j--){//打印第三条边
res[i][j] = count++;
}
for(;i > startx; i--){//打印第四条边
res[i][j] = count++;
}
startx++;
starty++;
offset++;
}
return res;//输出结果
}
};这里用了一个取巧的办法,是卡哥视频评论区朋友的建议,就是最开始初始化的时候,可以直接将所有值初始化为n的平方,这样即使最后一个值不进行输入,也正好就是需要的值,如果是偶数的话就只是重复赋值了一次而已。个人认为比较巧妙。
这道题目里面主要学习的点在于,慢慢理清每一条边在遍历赋值时的坐标变化,通过画图的方式逐步推理,遍历完一圈后,内部圈坐标的变化。很多时候只用脑子想会很绕,这时候画图并记录就会清晰很多。
数组内容结束了,这里引用代码随想录知识星球海螺人大佬制作的图片,作为以后复习时的材料。
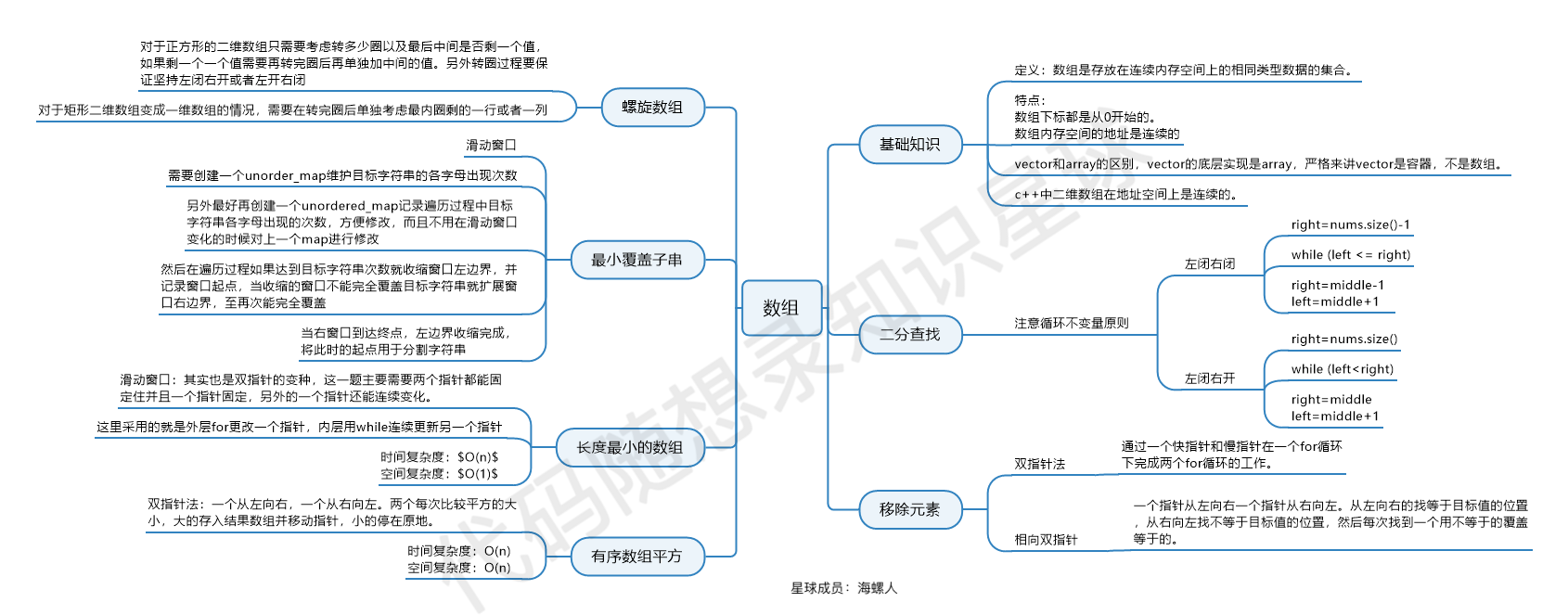
感谢大佬总结的知识导图!
一刷暂时就不做拓展题了,先把基础部分好好理清。由于代码基本功比较弱,很多地方都要自己去研究一下,力求把每一份代码中每一个部分都搞懂。