Transformer中的位置编码(Positional Encoding)

Mintisn / 2024-10-23 / 原文

Transformer中的位置编码(Positional Encoding)

标准位置编码

原理上Transformer是无法隐式学到序列的位置信息的，为了可以处理序列问题，Transformer提出者的解决方案是使用位置编码（Position Encode/Embedding，PE) . 大致的处理方法是使用sin和cos函数交替来创建位置编码PE, 计算公式如下:

\[PE_{t,2i}=\sin(t/10000^{2i/d}),\\PE_{t,2i+1}=\cos(t/10000^{2i/d}), \]

在这个公式中, $t$ 表示的是token的位置, $i$ 表示的是位置编码的维度

他的最终可视化效果长这样

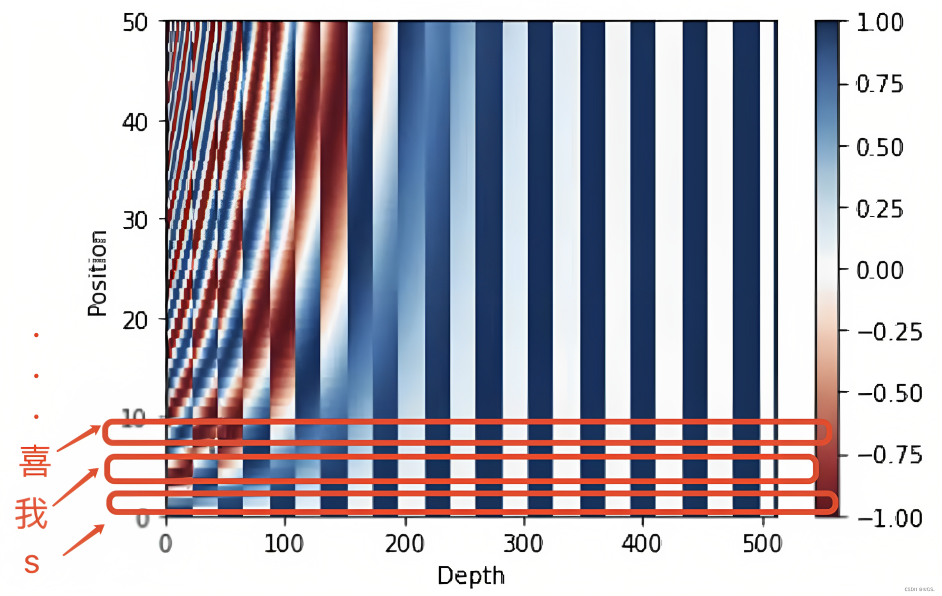
位置编码的作用, 就简而言之就是将每个位置编号，从而每个编号对应一个向量，最终通过结合位置向量和词向量，作为输入embedding，就给每个词都引入了一定的位置信息，这样Attention就可以分辨出不同位置的词了[^{3],这篇文章[}3]有标准位置编码的具体实现.

旋转位置编码($RoPE$)

旋转位置编码引入了复数的思想,在中这篇博客中比较详细的介绍了旋转位置编码的推导和实现. 首先需要对欧拉公式, 复数空间和旋转的关系有一个基本的理解

在transformer 的计算自注意力机制的过程中, 我们需要把query向量$q_m$ 和key向量$k_n$ 进行内积的操作

我们把q,k嵌入位置信息后表示为

\[\boldsymbol{q}_{m}=f_{q}(\boldsymbol{x}_{m},m)\\\boldsymbol{k}_{n}=f_{k}(\boldsymbol{x}_{n},n) \]

我们自然是希望, 在进行自注意的内积计算时, 能够保存两个向量间的相对位置信息, 这其实就是$RoPE$最求的目标:

\[<f_q\left(x_m,m\right),f_k\left(x_n,n\right)>=g\left(x_m,x_n,m-n\right) \]

$RoPE$的操作可以表示为:

\[f_{\{q,k\}}\left(\boldsymbol{x}_m,m\right)=R_{\Theta,m}^dW_{\{q,k\}}\boldsymbol{x}_m \]

其中

\[\left.\boldsymbol{R}_{\Theta,m}^{d}=\underbrace{\left(\begin{array}{ccccccc}\cos m\theta_0&-\sin m\theta_0&0&0&\cdots&0&0\\\sin m\theta_0&\cos m\theta_0&0&0&\cdots&0&0\\0&0&\cos m\theta_1&-\sin m\theta_1&\cdots&0&0\\0&0&\sin m\theta_1&\cos m\theta_1&\cdots&0&0\\\vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\0&0&0&0&\cdots&\cos m\theta_{d/2-1}&-\sin m\theta_{d/2-1}\\0&0&0&0&\cdots&\sin m\theta_{d/2-1}&\cos m\theta_{d/2-1}\end{array}\right)}_{\boldsymbol{w}_m}\right) \]

将词嵌入向量元素按照两两一组分组, 每组表示为表示为二维情形的拼接,相当于两两构成一个二位向量进行旋转操作

每组旋转的角度:

\[m\Theta=\begin{Bmatrix}m\theta_i=m10000^{-2(i-1)/d},i\in[1,2,\dots,d/2]\end{Bmatrix} \]

这篇博客还介绍了 LlaMA2 Long中对于位置编码的修改,即把基频(base frequency) 从10,000增加到500,000, 从而减少了每个维度的旋转角度

TODO 我并不明白这样修改为什么可以解决RoPE的局限性(即阻止注意力模块聚集远处token的信息),也没有更深入的了解(ref5,6) 目前的理解就是减少旋转角度,避免位置编码对原本编码产生太大的影响

reference

[1706.03762] Attention Is All You Need (arxiv.org)
Transformer改进之相对位置编码(RPE) - 知乎 (zhihu.com)
一文通透位置编码：从标准位置编码、旋转位置编码RoPE到ALiBi、LLaMA 2 Long(含NTK-aware简介)-CSDN博客
为什么说e^iθ就是在复数空间逆时针旋转角度θ？_复数逆时针旋转公式-CSDN博客求导,从物理的角度能够有很直观的解释
NTK-Aware Scaled RoPE 允许 LLaMA 模型具有扩展的（8k+）上下文大小，而无需任何微调和最小的困惑度降级。： r/LocalLLaMA --- NTK-Aware Scaled RoPE allows LLaMA models to have extended (8k+) context size without any fine-tuning and minimal perplexity degradation. : r/LocalLLaMA (reddit.com)
大模型长度扩展综述：从直接外推ALiBi、插值PI、NTK-aware插值(对此介绍最详)、YaRN到S2-Attention-CSDN博客