P5690 [CSP-S2019 江西] 日期 &&P7909 [CSP-J 2021] 分糖果 &&P5657 [CSP-S2019] 格雷码
今天继续懒惰,继续三合一!!!
[CSP-S2019 江西] 日期
题目背景
CSP-SJX2019 T1
题目描述
Alice在纸上写下了一个日期,形式为 \(\text{MM-DD}\),其中 \(\text{MM}\) 与 \(\text{DD}\) 都是两位数字,分别表示月和天,然而这个日期并不一定存在。 Alice找来了Bob要他更改若干位上的数字,使得这个日期存在。请你帮Bob算算他最少需要更改几位数字。
本题中我们认为 \(2\) 月固定为 \(28\) 天。
输入格式
仅一行一个五个字符的字符串,表示 \(\text{MM-DD}\) 。
输出格式
仅一行一个整数,表示答案。
样例 #1
样例输入 #1
03-32
样例输出 #1
1
样例 #2
样例输入 #2
02-39
样例输出 #2
1
样例 #3
样例输入 #3
67-89
样例输出 #3
2
提示
【输入输出样例1说明】
更改方式不止一种,其中一种方式是改为: \(\text{03-22}\)。
【输入输出样例2说明】
一种更改方式为:\(\text{02-09}\)。
【输入输出样例3说明】
一种更改方式为:\(\text{07-09}\)。
【数据规模与约定】
对于 \(100\%\) 的数据:\(\text{MM}\) 与 \(\text{DD}\) 一定为 \(4\) 个数字。
update: 2024/07/04 增加 hack 一组
思路
这道题一看发现只要一吨if就可以直接做出来了,情况也不是太多
1.首先我们看日期,可以发现,只要改第一位就一定可以做对
2.日期也受月份的限制所以要判断大月、小月和二月
3.题里面并没有给数据,所以有可能有负数,保险加特判
综上所述,我们可以得到如下程序:
#include<bits/stdc++.h>
using namespace std;
int main(){
freopen("date.in","r",stdin);
freopen("date.out","w",stdout);
int d,m;
scanf("%d-%d",&m,&d);
if(d==29||d==30){
if(m!=2&&m>0&&m<=12){
cout<<0;
return 0;
}
cout<<1;
return 0;
}
if(d>0&&d<=28){
if(m>0&&m<=12){
cout<<0;
return 0;
}
cout<<1;
return 0;
}
if(d==31){
if(m==2||m==4||m==6||m==9||m==11||m>=13&&m<=19){
cout<<1;
return 0;
}
if(m==1||m==3||m==5||m==7||m==8||m==10||m==12){
cout<<0;
return 0;
}
if(m%10==4||m%10==6||m%10==9){
cout<<2;
return 0;
}
cout<<1;
return 0;
}
if(m==0||m>12){
cout<<2;
return 0;
}
cout<<1;
return 0;
}
[CSP-J 2021] 分糖果
题目背景
红太阳幼儿园的小朋友们开始分糖果啦!
题目描述
红太阳幼儿园有 \(n\) 个小朋友,你是其中之一。保证 \(n \ge 2\)。
有一天你在幼儿园的后花园里发现无穷多颗糖果,你打算拿一些糖果回去分给幼儿园的小朋友们。
由于你只是个平平无奇的幼儿园小朋友,所以你的体力有限,至多只能拿 \(R\) 块糖回去。
但是拿的太少不够分的,所以你至少要拿 \(L\) 块糖回去。保证 \(n \le L \le R\)。
也就是说,如果你拿了 \(k\) 块糖,那么你需要保证 \(L \le k \le R\)。
如果你拿了 \(k\) 块糖,你将把这 \(k\) 块糖放到篮子里,并要求大家按照如下方案分糖果:只要篮子里有不少于 \(n\) 块糖果,幼儿园的所有 \(n\) 个小朋友(包括你自己)都从篮子中拿走恰好一块糖,直到篮子里的糖数量少于 \(n\) 块。此时篮子里剩余的糖果均归你所有——这些糖果是作为你搬糖果的奖励。
作为幼儿园高质量小朋友,你希望让作为你搬糖果的奖励的糖果数量(而不是你最后获得的总糖果数量!)尽可能多;因此你需要写一个程序,依次输入 \(n, L, R\),并输出你最多能获得多少作为你搬糖果的奖励的糖果数量。
输入格式
输入一行,包含三个正整数 \(n, L, R\),分别表示小朋友的个数、糖果数量的下界和上界。
输出格式
输出一行一个整数,表示你最多能获得的作为你搬糖果的奖励的糖果数量。
样例 #1
样例输入 #1
7 16 23
样例输出 #1
6
样例 #2
样例输入 #2
10 14 18
样例输出 #2
8
样例 #3
样例输入 #3
见附件中的 candy/candy3.in。
样例输出 #3
见附件中的 candy/candy3.ans。
提示
【样例解释 #1】
拿 \(k = 20\) 块糖放入篮子里。
篮子里现在糖果数 \(20 \ge n = 7\),因此所有小朋友获得一块糖;
篮子里现在糖果数变成 \(13 \ge n = 7\),因此所有小朋友获得一块糖;
篮子里现在糖果数变成 \(6 < n = 7\),因此这 \(6\) 块糖是作为你搬糖果的奖励。
容易发现,你获得的作为你搬糖果的奖励的糖果数量不可能超过 \(6\) 块(不然,篮子里的糖果数量最后仍然不少于 \(n\),需要继续每个小朋友拿一块),因此答案是 \(6\)。
【样例解释 #2】
容易发现,当你拿的糖数量 \(k\) 满足 \(14 = L \le k \le R = 18\) 时,所有小朋友获得一块糖后,剩下的 \(k - 10\) 块糖总是作为你搬糖果的奖励的糖果数量,因此拿 \(k = 18\) 块是最优解,答案是 \(8\)。
【数据范围】
| 测试点 | \(n \le\) | \(R \le\) | \(R - L \le\) |
|---|---|---|---|
| \(1\) | \(2\) | \(5\) | \(5\) |
| \(2\) | \(5\) | \(10\) | \(10\) |
| \(3\) | \({10}^3\) | \({10}^3\) | \({10}^3\) |
| \(4\) | \({10}^5\) | \({10}^5\) | \({10}^5\) |
| \(5\) | \({10}^3\) | \({10}^9\) | \(0\) |
| \(6\) | \({10}^3\) | \({10}^9\) | \({10}^3\) |
| \(7\) | \({10}^5\) | \({10}^9\) | \({10}^5\) |
| \(8\) | \({10}^9\) | \({10}^9\) | \({10}^9\) |
| \(9\) | \({10}^9\) | \({10}^9\) | \({10}^9\) |
| \(10\) | \({10}^9\) | \({10}^9\) | \({10}^9\) |
对于所有数据,保证 \(2 \le n \le L \le R \le {10}^9\)。
【感谢 hack 数据提供】
wangbinfeng
暴力做法:
既然拿的糖是从l——r那么我们直接枚举每一个数然后找最大不就好了吗?
代码非满分,所有的没有展示的AC代码会每一段时间汇总发出
#include <bits/stdc++.h>
using namespace std;
int main(){
freopen("candy.in","r",stdin);
freopen("candy.out","w",stdout);
int ans=-0x7fffffff;
int n,l,r;
cin>>n>>l>>r;
for(int i=l;i<=r;i++){
ans=max(i%n,ans);
}
cout<<ans;
return 0;
}
[CSP-S2019] 格雷码
题目描述
通常,人们习惯将所有 \(n\) 位二进制串按照字典序排列,例如所有 2 位二进制串按字典序从小到大排列为:00,01,10,11。
格雷码(Gray Code)是一种特殊的 \(n\) 位二进制串排列法,它要求相邻的两个二进制串间恰好有一位不同,特别地,第一个串与最后一个串也算作相邻。
所有 2 位二进制串按格雷码排列的一个例子为:00,01,11,10。
\(n\) 位格雷码不止一种,下面给出其中一种格雷码的生成算法:
- 1 位格雷码由两个 1 位二进制串组成,顺序为:0,1。
- \(n + 1\) 位格雷码的前 \(2^n\) 个二进制串,可以由依此算法生成的 \(n\) 位格雷码(总共 \(2^n\) 个 \(n\) 位二进制串)按顺序排列,再在每个串前加一个前缀 0 构成。
- \(n + 1\) 位格雷码的后 \(2^n\) 个二进制串,可以由依此算法生成的 \(n\) 位格雷码(总共 \(2^n\) 个 \(n\) 位二进制串)按逆序排列,再在每个串前加一个前缀 1 构成。
综上,\(n + 1\) 位格雷码,由 \(n\) 位格雷码的 \(2^n\) 个二进制串按顺序排列再加前缀 0,和按逆序排列再加前缀 1 构成,共 \(2^{n+1}\) 个二进制串。另外,对于 \(n\) 位格雷码中的 \(2^n\) 个 二进制串,我们按上述算法得到的排列顺序将它们从 \(0 \sim 2^n - 1\) 编号。
按该算法,2 位格雷码可以这样推出:
- 已知 1 位格雷码为 0,1。
- 前两个格雷码为 00,01。后两个格雷码为 11,10。合并得到 00,01,11,10,编号依次为 0 ~ 3。
同理,3 位格雷码可以这样推出:
- 已知 2 位格雷码为:00,01,11,10。
- 前四个格雷码为:000,001,011,010。后四个格雷码为:110,111,101,100。合并得到:000,001,011,010,110,111,101,100,编号依次为 0 ~ 7。
现在给出 \(n\),\(k\),请你求出按上述算法生成的 \(n\) 位格雷码中的 \(k\) 号二进制串。
输入格式
仅一行两个整数 \(n\),\(k\),意义见题目描述。
输出格式
仅一行一个 \(n\) 位二进制串表示答案。
样例 #1
样例输入 #1
2 3
样例输出 #1
10
样例 #2
样例输入 #2
3 5
样例输出 #2
111
样例 #3
样例输入 #3
44 1145141919810
样例输出 #3
00011000111111010000001001001000000001100011
提示
【样例 1 解释】
2 位格雷码为:00,01,11,10,编号从 0∼3,因此 3 号串是 10。
【样例 2 解释】
3 位格雷码为:000,001,011,010,110,111,101,100,编号从 0∼7,因此 5 号串是 111。
【数据范围】
对于 \(50\%\) 的数据:\(n \leq 10\)
对于 \(80\%\) 的数据:\(k \leq 5 \times 10^6\)
对于 \(95\%\) 的数据:\(k \leq 2^{63} - 1\)
对于 \(100\%\) 的数据:\(1 \leq n \leq 64\), \(0 \leq k \lt 2^n\)
思路
可以直接用搜索,暴力枚举,生成格雷码的方法:
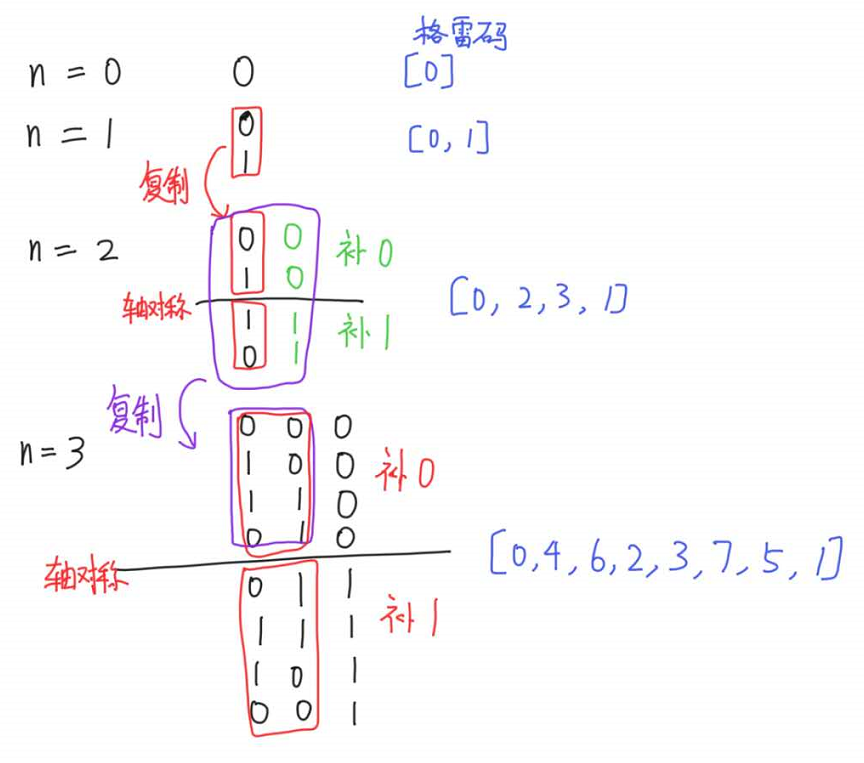
根据题意,我们还可以发现:如果要求n位格雷码的第k个,那么k<2^n的一半,这一位就生成0,如果k>= 2^n的一半,就生成1
综上所述,我们可以得到如下程序:
#include <bits/stdc++.h>
using namespace std;
#define ll unsigned long long
int n;
ll k;
void dfs(int x,ll y){
if(x==1){
cout<<y;
return ;
}
long long half=pow(2,x-1);
if(y<half){
cout<<"0";
dfs(x-1,y);
}else if(k>=half){
cout<<"1";
long long a=y-half;
dfs(x-1,half-1-a);
}
}
int main(){
cin>>n>>k;
dfs(n,k);
return 0;
}