KMP 以及 border 性质的一些运用

endswitch / 2024-10-23 / 原文

一个 kmp 学了 $n$ 遍终于学懂的屑菜 bot。

下文默认文本串为 $s$，模式串为 $t$。

前缀函数

定义

$\pi_i$ 表示前缀为 $i$ 的子串中的最长公共前后缀（border）长度。

求取

暴力

$O(n ^ 3)$ 去暴力枚举。

高效算法

第一个重要的观察是相邻的前缀函数值至多增加 $1$。

那么我们就是要往前查找一个尽可能大的 $\pi$ 满足其往后一位仍然能匹配，或直到 border 长度为 $0$。

具体地可以依照这个视频来看，讲得非常详细。

模板

不难发现实现起来非常之短。

n = s.size(), m = t.size();
	
	s = t + '?' + s;
	
	for(int i = 1, j = nxt[i - 1] ; i < (int)s.size() ; ++ i) {
		while(j && s[i] != s[j]) j = nxt[j - 1];
		
		if(s[i] == s[j]) {
			nxt[i] = ++ j;
			
			if(nxt[i] == m) cout << i - m * 2 + 1 << '\n', j = nxt[j - 1];
		} 
	}

KMP

不难发现，将文本串接在模式串后，中间隔一个特殊字符，若出现 $\pi_i = |t|$ 的情况则说明匹配成功了。

例题

CF126B

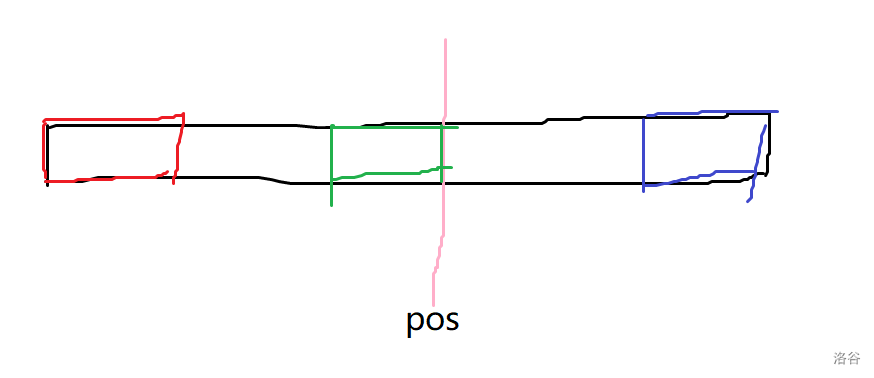
如图，pos 为当前枚举到的位置，红色部分和蓝色部分为 $[1, pos]$ 的 border，那么不难发现红 = 蓝 = 绿。

正序、倒序各求一遍 border 即可。

for(int i = 2 ; i < n ; ++ i)
	if(nxt[i][0] == nxt[n - i + nxt[i][0]][1])
		if(nxt[i][0] > ans) {
			ans = nxt[i][0];

			pos = i;
		}

if(! ans) cout << "Just a legend";
else
	for(int i = 0 ; i < nxt[pos][0] ; ++ i)
		cout << s[i];