支持向量机 --优化
支持向量机
1. 支持向量
SVM 最优化问题
SVM 想要的就是找到各类样本点到超平面的距离最远，也就是找到最大间隔超平面。任意超平面可以用下面这个[线性方程]来描述：
\[\omega ^ T x +b=0
\]
二维空间点$ (x,y)$ 到直线$ Ax+By+C=0$ 的距离公式是：
\[\frac{|Ax+By+C|}{\sqrt{A^2+B^2}}
\]
扩展到 n 维空间后，点\(x=(x_1,x_2\ldots x_n)\)到直线\(w^Tx+b=0\)的距离为
\[\frac{|w^Tx+b|}{||w||}
\]
其中 $ \left|\left|w\right|\right|=\sqrt{w_{1}^{2}+\ldots w_{n}^{2}} $
如图所示，根据支持向量的定义我们知道，支持向量到超平面的距离为 d，其他点到超平面的距离大于 d。
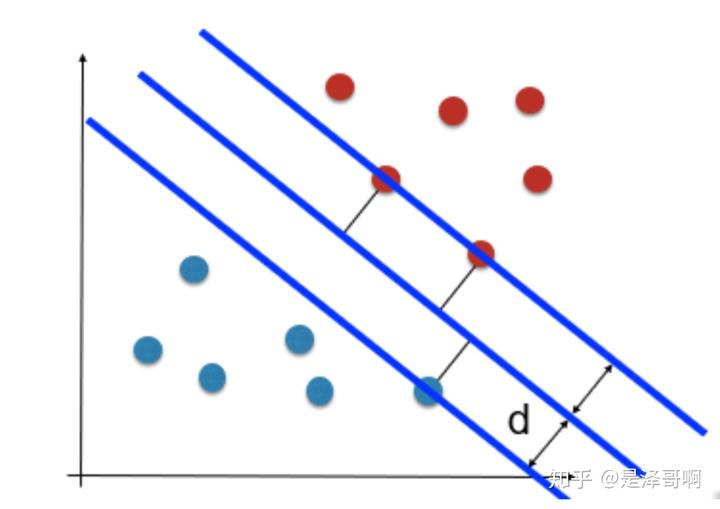
于是我们有这样的一个公式：
\[\begin{cases}
\frac{w^Tx+b}{||w||}\geq d \quad y=1\\
\frac{w^Tx+b}{||w||}\leq-d \quad y=-1
\end{cases}
\]
稍作转化可以得到：
\[\begin{cases}\frac{w^Tx+b}{||w||d}\geq1\quad y=1\\\frac{w^Tx+b}{||w||d}\leq-1\quad y=-1\end{cases}
\]
\(||\omega||d\)是正数，我们暂且令它为 1（之所以令它等于 1，是为了方便推导和优化，且这样做对[目标函数]的优化没有影响），
故：
\[\left\{\begin{matrix}
{w^{T}x+b\geq1\quad y=1}\\
{w^{T}x+b\leq-1\quad y=-1}\\
\end{matrix}\right.
\]
将两个方程合并，我们可以简写为：
\[y(\omega ^T x+b) \geq 1
\]
至此我们就可以得到最大间隔超平面的上下两个超平面：
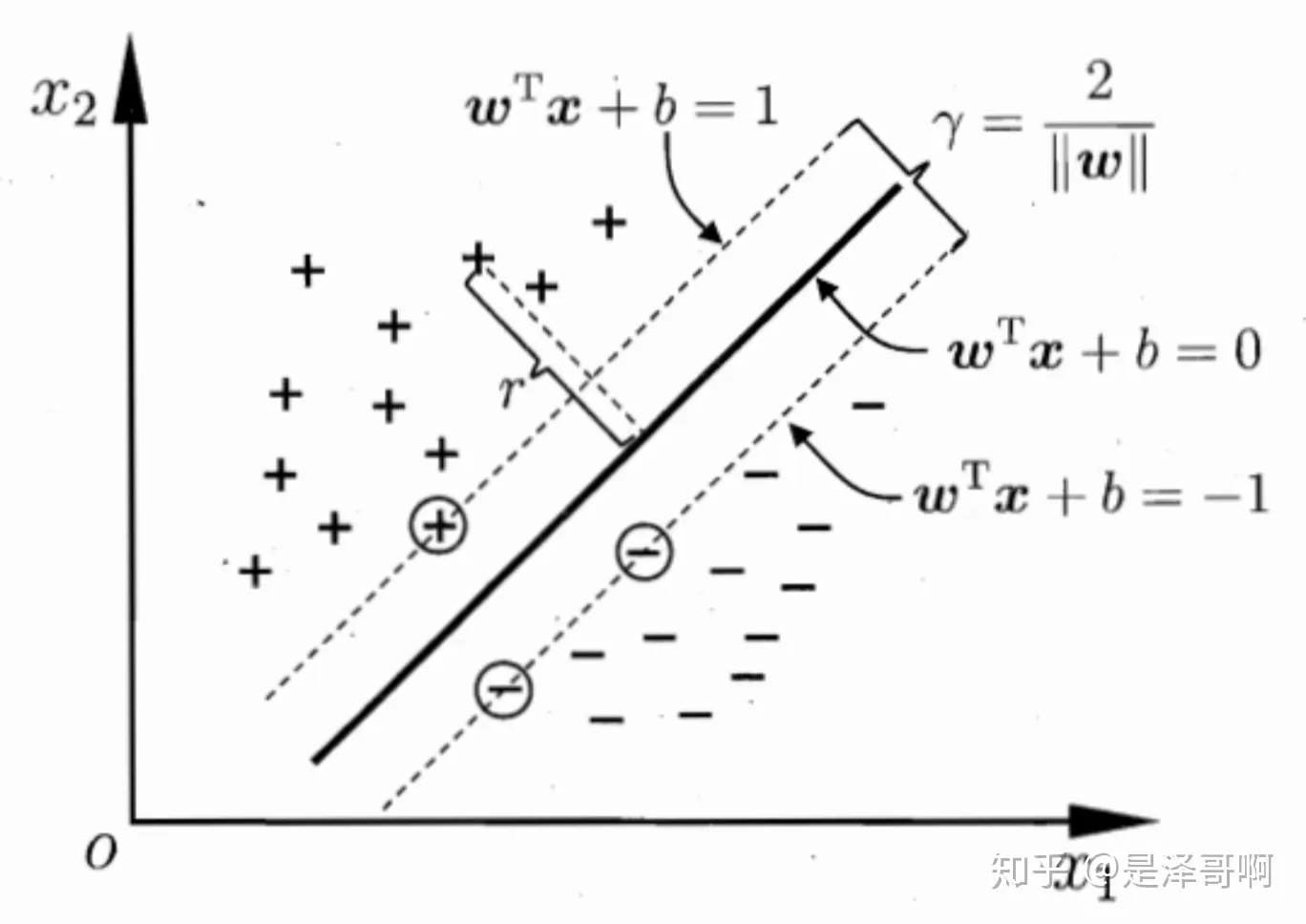
每个支持向量到超平面的距离可以写为：
\[d=\frac{|w^{T}x+b|}{||w||}
\]
由上述\(y(w^Tx+b)>1>0\)可以得到\(y(w^Tx+b)=|w^Tx+b|\) ,所以我们得到：
\[d=\frac{y(w^{T}x+b)}{||w||}
\]
最大化这个距离：\(\max2*\frac{\nu(w^Tx+b)}{||w||}\)
这里乘上 2 倍也是为了后面推导，对目标函数没有影响。刚刚我们得到支持向量\(y(w^Tx+b)=1\).
所以我们得到：\(max \frac {2}{||\omega||}\)
再做一个转换：\(min \frac {1}{2}||\omega||\)
为了方便计算（去除 \(||\omega||\) 的根号）,
我们有：\(min \frac {1}{2}||\omega||^2\)
所以得到优化问题：
\[min \frac{1}{2}||\omega||^2 s.t. \\
y_i(\omega ^T x_i +b)
\]