A.带余除法

我们不难考虑找出 \(q\) 的上下界，不难发现范围是 \([\lfloor\frac{n}{k+1}\rfloor+1,\lfloor\frac{n}{k}\rfloor]\)。当然这个区间可能为空。只需算出区间长度即可。

B.奖牌排序

不难考虑到分别按照三个关键字排序，然后对于每个小朋友找到每个关键字下的排名（同分取第一个），取一个最小值就做完了。

C.三目运算

每年必出的大模拟，但这题好像还有图论？我们考虑找出每个 ? 匹配的 :，这个是不难做的，用一个栈就行。

接下来考虑把一个分段常数表达式看成三部分：? 前面的，? 和 : 之间的，: 后面的，记为 \(u,a,b\)。

接下来考虑 \(u\) 对 \(a,b\) 分别连边，就形成了一棵树。于是暴力就是好想的了，每次询问遍历一遍树。但是这样很容易被卡，例如下面这样：

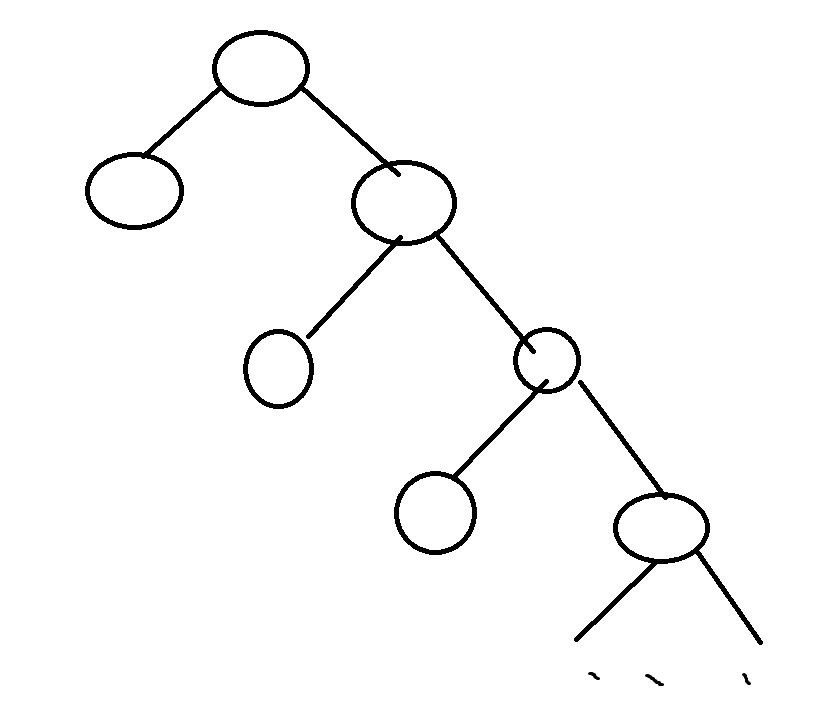
这种结构会导致每次遍历是 \(O(n)\) 的，直接超时。于是考虑怎么优化。

发现慢的原因是每次询问都要遍历一次树，那么考虑所有询问一起遍历。

具体地，把所有询问离线下来，扔到一个序列里排序去重，每个树上的点必然把一部分分到左子节点，另外一部分分到右子节点。只需要记录这个点处理的是序列中的 \([l,r]\) 部分就可以完成划分操作。到达叶子节点直接赋值即可。其实上面的过程就是整体二分。

D.配对序列

看到最优化问题，不难想到贪心或者动态规划。仔细构造几组样例就可以发现贪心假了，于是考虑动态规划。

设 \(f_{i,0}\) 表示第 \(i\) 个位置作为一个子序列的开头，已经凑出来的配对子序列的长度最大是多少；\(f_{i,0}\) 表示第 \(i\) 个位置作为一个子序列的结尾，已经凑出来的配对子序列的长度最大是多少。

不难得出转移方程：\(\displaystyle f_{i,0}=\max_{j<i}(f_{j,1})\)，其中 \(a_j\ne a_i\)；\(\displaystyle f_{i,1}=\max_{j<i}(f_{j,0})+2\)，其中 \(a_j=a_i\)。

暴力转移时间复杂度是 \(O(n^2)\) 的，考虑数据结构。发现最值可以使用线段树维护，只需要把原序列离散化然后使用线段树转移即可。第 \(j\) 棵线段树的 \(i\) 节点存的值为 \(f_{i,j-1}\)，其中 \(j=1\) 或 \(j=2\)。

E.商店砍价

不难观察出一个结论：最后剩下一起的数不会太大，事实上最多只有 \(5\) 位，于是只需要枚举剩下的东西是什么并判断这个东西在不在整个串里即可。

F.水杯降温

首先有一个简单的小性质，我们改变操作的顺序不会造成影响。于是我们不妨设先进行操作二再进行操作一。于是考虑什么情况下只做操作一也合法。

不难发现父亲节点的值不能小于子节点的值，因为只可能出现子节点加的东西不少于父亲节点加的东西的情况。同时需要满足根节点的值不大于 \(0\)。

于是我们考虑每个 \(x\) 点最多能被操作一减少多少还满足有解的要求，设这个数组为 \(f_x\)。不难发现 \(f\) 数组可以二分求出。

假设我们当前二分到的 \(f_x\) 的值为 \(m\)，设 \(y\) 为 \(x\) 的子节点。考虑 \(m\) 什么情况下合法：

• \(m\le \sum f_y\)。

• \(m\ge \sum \max(0,a_y-(a_x-m))\)。

• \(a_y-(a_x-m)\le f_y\)。

于是最后有解的要求就是 \(f_1\ge a_1\)。

G.反回文串

特殊性质给的相当好的一道题。遇到这种神秘构造一般特殊性质都会有一些提示，所以先看特殊性质。

下面记出现次数不小于 \(\lfloor\frac{n+1}{2}\rfloor\) 的字母为绝对众数。

不难得出 \(A\) 性质可以近似看成没有绝对众数（前提是 \(n\) 为偶数）。于是我们简单讨论一下不存在绝对众数的做法：

考虑把所有字母按照字典序存进数组 \(a\) 里，于是 \(a_i\) 和 $a_{i+\lfloor\frac{siz}{2}\rfloor} 配对即可。但是这样可能会剩下一个字母 \(a_{siz}\)，把他扔到 \(a_1\) 所在的组即可。这样能分出来 \(\lfloor\frac{n}{2}\rfloor\) 组。

下面讨论一下存在绝对众数的做法：

不妨设绝对众数所在字母为 \(x\)，其他字母为 \(y\)，不难发现每一组至少有一个 \(y\)，否则会出现整个组的字母全部相同的情况。

首先特判绝对众数出现的次数不小于 \(siz-1\) 的情况。接下来我们设第一个 \(y\) 出现的位置为 \(l\)，最后一个 \(y\) 出现的位置为 \(r\)。考虑用两个数组分别加入 \(l\)，\(l\) 前面的 \(x\) 和 \(r\)，\(l\) 后面的 \(x\)。

剩下的 \(y\) 每一个都新开一部分，如果那部分没有 \(x\) 的话就尝试从前两个数组中拿一个即可。这样能分出来 \(y\) 的数量组。

H.超级演出

我们先考虑一个比较优秀的暴力。离线下来所有询问，从序列头扫描到序列尾，对于每个点 \(r\) 找出一个最大的点 \(l\)，使得 \([l,r-1]\) 区间内的所有东西被加入后，\(r\) 也可以被加入。我们令 \(las_r=l\)。

只需要每次加入一个点的时候使用其出点进行更新即可。同时设当前的点为 \(r\)，那么对于所有询问 \([l,r]\)，用树状数组查询有多少 \(las\) 在 \([l,r]\) 内即可得到 \(76\) 分。

不难发现这样做的瓶颈在于每次用出点更新自己的过程。因为如果这个点的出度非常大，时间复杂度就是平方级别的了。

于是我们考虑根号分治。设 \(t=\sqrt m\)。对于出度不超过 \(t\) 的点，用上述方法暴力更新即可。否则我们开一个 \(top\) 数组暂存 \(las\)，\(top\) 是用其入点的 \(las\) 更新的。而当我们遇到一个出度超过 \(t\) 的点 \(x\) 的时候，就把 \(top_x\) 赋值过去。这样复杂度就是对的了。