Codeforces Round 978 (Div. 2) A-D1 题解
A. Bus to Pénjamo
题意
有一辆车上面有 \(r\) 排座位,每排有 \(2\) 个座位,现在共 \(n\) 个家庭出行坐公交车,每个家庭 \(a_i\) 个人(保证 \(2r\ge \sum a_i\))。
一个人感到 开心,当且仅当符合一下条件 之一:
- 他和他的家庭成员坐在一排
- 他独自一人坐在一排(旁边不能有其他人)
问最终最多有多少人 开心
思路
贪心,先让可以两个人一排的家庭成员入座,剩下的看 \([座位数]\) 与 \([剩余人数]\) 的差,得出有多少人能单独坐一排
C++ 代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,r;
void solve(){
cin>>n>>r;
int k=0;
int ans=0;
for(int i=0;i<n;i++){
int ai;
cin>>ai;
k+=(ai%2); //k表示每个家庭落单的人数
r-=(ai/2); //r最终表示还剩下几排座位
ans+=ai-ai%2;
}
r*=2; //还剩r个座位
ans+=min(r-k,k);
cout<<ans<<endl;
}
signed main(){
int t;
cin>>t;
while(t--){
solve();
}
return 0;
}
B. Kar Salesman
题意
共有 \(n\) 中型号的车,第 \(i\) 种型号的车有 \(a_i\) 辆,每次 \(\text{Karel}\) 可以推荐别人购买至多 \(x\) 辆车,且这些为 不同型号
问至少要推销给多少个人才能卖完这些车
思路
求出车数量的总和(设为 \(sum\) ),和 \(a_i\) 的最大值(设为 \(mx\)),最终答案为:\(\displaystyle \max(mx,\lceil \frac{sum}{x} \rceil)\)
C++ 代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
void solve(){
int n,x;
cin>>n>>x;
int mx=0,sum=0;
for(int i=0;i<n;i++){
int ai;
cin>>ai;
mx=max(mx,ai);
sum+=ai;
}
cout<<max(mx,(sum+x-1)/x)<<endl;
}
signed main(){
int t;
cin>>t;
while(t--){
solve();
}
return 0;
}
C. Gerrymandering
题意
一个 \(2*n\) 的网格图,每格代表一个居民(需要进行投票选举,可以投给 A 也可以投给 J),保证 \(2n \bmod 3 =0\),将它分成 连通的 \(3\) 个一组,这一组 将投给 三个人投的更多的人,如 \(2\) 个 A \(1\) 个 J,则这一组投给 A
问:若按最优方案分组,最终投给 \(A\) 的组最多有多少
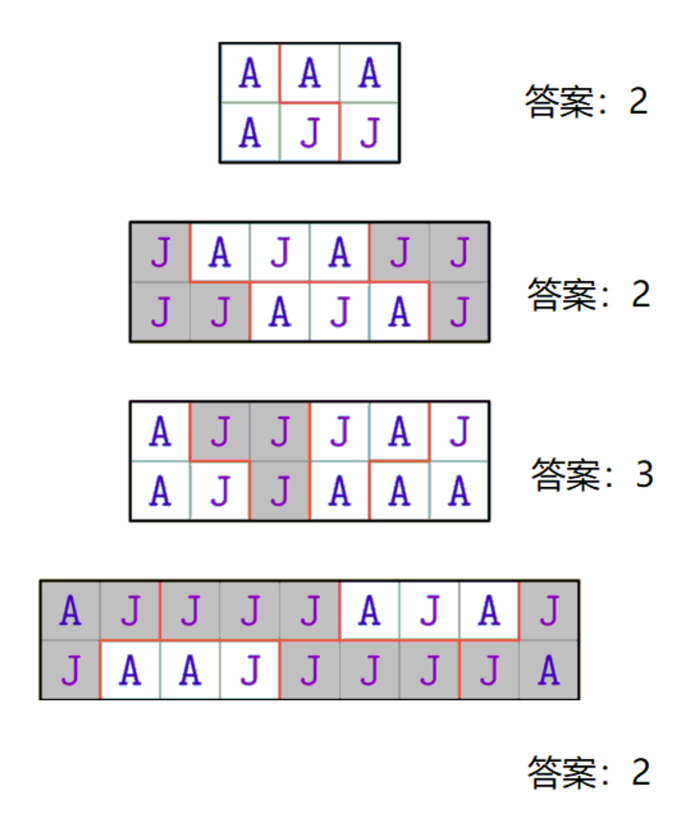
思路
需要动态规划,仅分为以下情况:
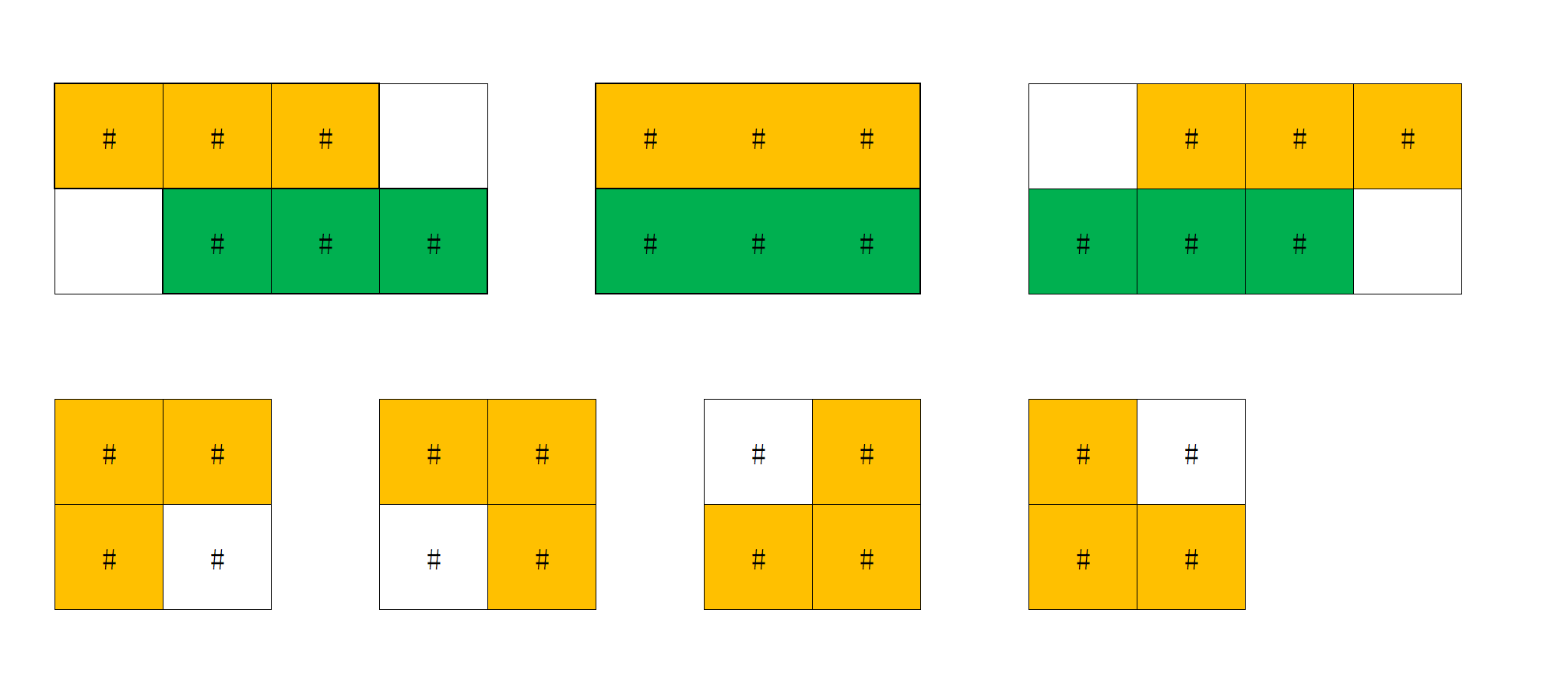
那么,只要转移正确就很简单
转移直接看代码
C++ 代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int inf=2e9;
int n;
bool check(int a,int b,int c){
int p=(a=='A'),q=(b=='A'),r=(c=='A');
return (p+q+r>=2);
}
void solve(){
cin>>n;
string s[2];
cin>>s[0]>>s[1];
vector<vector<int> > dp(2,vector<int>(n+1,-inf));
dp[0][0]=0;
for(int i=0;i<n;i++){
if(i%3==0){
dp[0][i+3]=max(dp[0][i+3],
dp[0][i]+check(s[0][i],s[0][i+1],s[0][i+2]) //###
+check(s[1][i],s[1][i+1],s[1][i+2])); //###
dp[0][i+1]=max(dp[0][i+1], //##
dp[0][i]+check(s[0][i],s[1][i],s[0][i+1])); //#.
dp[1][i+1]=max(dp[1][i+1], //#.
dp[0][i]+check(s[0][i],s[1][i],s[1][i+1])); //##
}else if(i%3==1){
if(i<n-3){
dp[0][i+3]=max(dp[0][i+3],
dp[0][i]+check(s[0][i+1],s[0][i+2],s[0][i+3]) //.###
+check(s[1][i],s[1][i+1],s[1][i+2])); //###.
dp[1][i+3]=max(dp[1][i+3],
dp[1][i]+check(s[0][i],s[0][i+1],s[0][i+2]) //###.
+check(s[1][i+1],s[1][i+2],s[1][i+3])); //.###
}
dp[0][i+2]=max(dp[0][i+2], //.#
dp[0][i]+check(s[1][i],s[1][i+1],s[0][i+1])); //##
dp[0][i+2]=max(dp[0][i+2], //##
dp[1][i]+check(s[0][i],s[0][i+1],s[1][i+1])); //.#
}
}
cout<<dp[0][n]<<endl;
}
signed main(){
int t
cin>>t;
while(t--){
solve();
}
return 0;
}
D1. Asesino (Easy Version)
题意
这是一道 交互题
有一种游戏,共有三种角色:Knight, Knave, Impostor,可以理解为:好人、坏人和内鬼
每局游戏有 \(n\) 个人,其中有 \(1\) 个内鬼,若干个好人和坏人(可能 \(0\) 个)
你忘记了每个人的角色,但是,你可以问玩家 \(i\) :玩家 \(j\) 是不是好人?询问格式:? i j
玩家 \(i\) 会回答你 1 表示是好人,0 表示不是好人
以下为不同身份的回答表格:
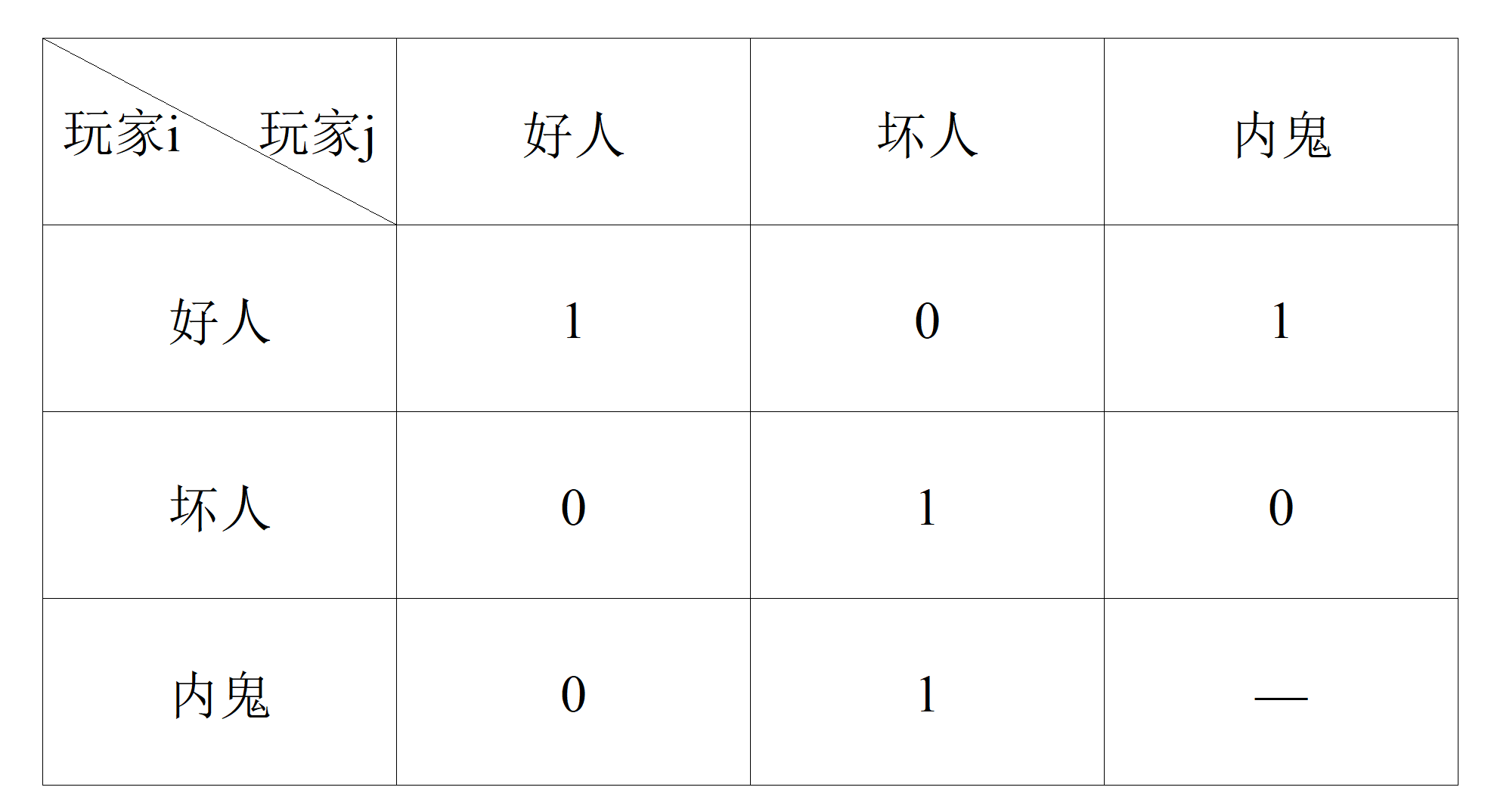
最多询问 \(n+69\) 次,请找出内鬼是玩家几,格式为 ! i
思路
观察表格发现,若 \([i\ 认为 \ j 的身份]\) 和 \([j \ 认为\ i\ 的身份]\) 不同,那么 \(i\) 和 \(j\) 中必定有一个内鬼
那么我们可以问每两个相邻的人,\(i\) 和 \(i+1\) 互相问,\(i+2\) 和 \(i+3\) 互相问,以此类推,最终找到 \(k\) 和 \(k+1\) 不同的位置,再和其他的比较,就可以得到内鬼的位置
C++ 代码
#include<bits/stdc++.h>
using namespace std;
int n;
bool query(int a,int b){
cout<<"? "<<a<<" "<<b<<endl;
int p;
cin>>p;
cout<<"? "<<b<<" "<<a<<endl;
int q;
cin>>q;
return p!=q;
}
void solve(){
cin>>n;
int pos=-1;
for(int i=1;i<n;i+=2){
bool flag=query(i,i+1);
if(flag){
pos=i;
break;
}
}
if(pos==-1){
cout<<"! "<<n<<endl;
}else if(query(pos,pos>1?pos-1:pos+2)){
cout<<"! "<<pos<<endl;
}else{
cout<<"! "<<pos+1<<endl;
}
}
int main(){
int t;
cin>>t;
while(t--){
solve();
}
return 0;
}