由于k最大为2500，故用三重循环暴力查找x，y，z复杂度为O（n^3）会超时。s已经是定值，故可以用技巧暴力查找x，y再看看所得到的z满不满足[0,k]即可

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN = 900;
int k, s; 
signed main(){
	cin >> k >> s;
	int ans = 0;
	for(int i = 0; i <= k; i++)
		for(int j = 0; j <= k; j++){
			int x = s - i - j;
			if(x >= 0 && x <= k) ans++;
		}
	cout << ans << endl;
	return 0;
}

利用cnt计数，ans随时记录最大值

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN = 900;
int n; 
signed main(){
	cin >> n;
	int cnt = 0, ans = 0;
	while(n--){
		char c;
		cin >> c;
		if(c == 'I') cnt++;
		else if(c == 'D') cnt--;
		ans = max(ans, cnt);
	}
	cout << ans << endl;
	return 0;
}

说实话这道题我也还没搞懂（汗，涉及数论知识大家可以点链接了解一下
https://blog.csdn.net/weixin_30240349/article/details/95853957

因为只需要至少达到x分而不是刚好达到x分，因此可以贪心的每次选择6和5（即11一周期）循环，最后看余数再判断需要再操作几次

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MOD = 1e9+7;
const int MAXN = 900;
int x;
signed main(){
	cin >> x;
	int a = x % 11;
	int t = x / 11;
	if(a == 0){
		cout << t * 2 << endl;
		return 0;
	}
	if(a <= 6) cout << t * 2 + 1 << endl; //一周期结束后的下一次操作是6
	else cout << t * 2 + 2 << endl;
	return 0;
}

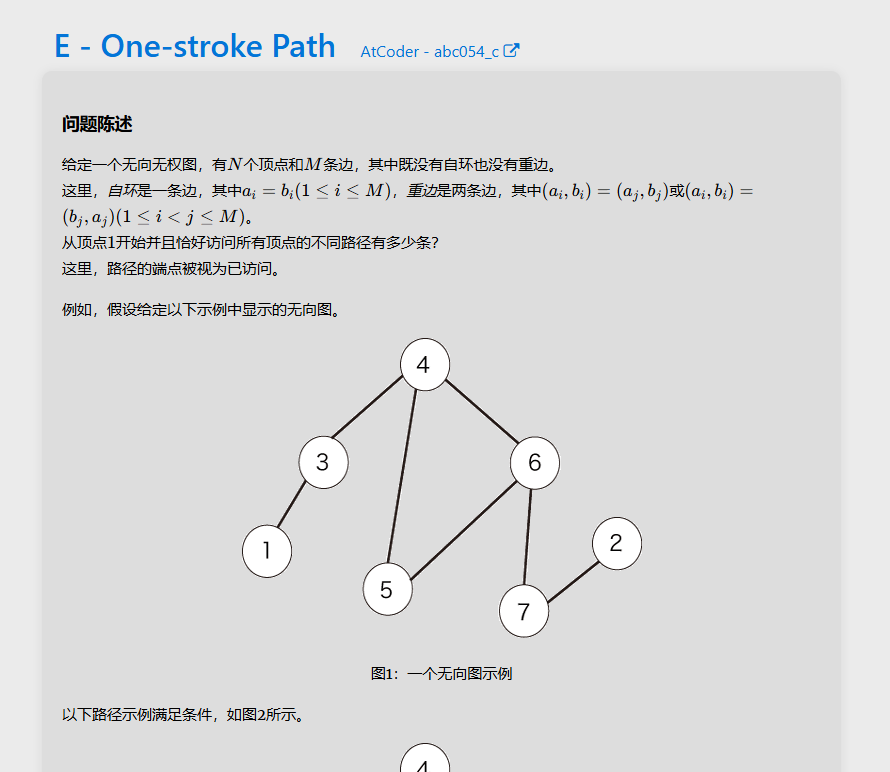
由于节点数很小（10以内），因此可以用dfs暴力求解，从节点1开始搜索，如果能使cnt == n就代表搜索所有节点成功

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MOD = 1e9+7;
const int MAXN = 900;
int n, m;
int ans;
bool a[10][10]; // 代表i->j有无道路，1表示有道路，由于道路双向，所以a[i][j]与a[j][i]一致
bool v[10];
void dfs(int i, int cnt){
	if(cnt == n){
		ans++;
		return;
	}
	for(int j = 1; j <= n; j++){
		if(a[i][j] && !v[j]){ //如果未访问过且可以到达j，则往下搜索
			v[j] = 1;
			dfs(j, cnt + 1);
			v[j] = 0;//记得回溯
		} 
	}
}
signed main(){
	cin >> n >> m;
	for(int i = 1; i <= m; i++){
		int x, y;
		cin >> x >> y;
		a[x][y] = 1;
		a[y][x] = 1;
	}
	v[1] = 1;
	dfs(1, 1);//根据题目意思从节点1开始搜索
	cout << ans << endl;
	return 0;
}

涉及floyd算法求任意两点最短路径，https://blog.csdn.net/qq_43753724/article/details/129507989
大致题意：求给定的每条边不是i点到j点的最短路径的总数
先用floyd算法求出任意两点的最短路径，再对每条边进行判断即可

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MOD = 1e9+7;
const int MAXN = 110;
const int N = 1010;
int n, m;
int x[N], y[N], d[N];
int dist[MAXN][MAXN];
void init(){
	for(int i = 1; i <= n; i++)
		for(int j = 1; j <= n; j++){
			if(i != j) dist[i][j] = 0x3f3f3f3f;
			else dist[i][j] = 0;
		}
}
void floyd(){
	for(int k = 1; k <= n; k++){
			for(int i = 1; i<=n; i++){
				for(int j = 1; j <= n; j++){
					dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);		
				}
			}
	}
}
signed main(){
	cin >> n >> m;
	init();
	for(int i = 1; i <= m; i++){
		cin >> x[i] >> y[i] >> d[i];
		dist[x[i]][y[i]] = d[i];
		dist[y[i]][x[i]] = d[i];
	}
	floyd();
	int ans = 0;
	for(int i = 1; i <= m; i++){
			if(d[i] > dist[x[i]][y[i]]) ans++;
	}
	cout << ans << endl;
	return 0;
}

贪心，比较走路的疲劳值和传送的疲劳值大小，谁小就用谁

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MOD = 1e9+7;
const int MAXN = 100005;
int n, x, y;
int d[MAXN]; //差分数组
signed main(){
	cin >> n >> x >> y;
	int now = 0, last = 1;
	for(int i = 1; i <= n; i++){
		cin >> now;
		d[i] = (now - last) * x; // 提前计算两个城市间走路需要的疲劳值
		last = now;
	}
	int ans = 0;
	for(int i = 2; i <= n; i++){
		ans += min(d[i], y);
	}
	cout << ans << endl;
	return 0;
}