YL 24-CSPS 模拟赛总结
说明
好吧,该说一下阅读指南了。里面都是我模拟赛的一些总结,主要总结自己,没有想写题解一样的描述,最多写一点解法。前面的 2024xxxx 是日期,后面的 YLOI-R? 是第几场。里面四道题用 \(\text{A, B, C, D}\) 表示每道题,祝阅读愉快。
以下是 notion.so 上的原说明:
此系列比赛由鸭梨官方举办,最终解释权为鸭梨恶臭公司。
说明:题目均为牛客 OI 赛前训练营的题。
20240923 YLOI-R1
依依寺(yiyi)
期望得分:\([40, 50]\),实际得分:\(0\)。
博弈论,个人觉得比较难,评个黄~绿。
一开始题目直接读错,以为是一个人可以取多个数,多个数的总和 \(\bmod\ 3\) 要 \(\neq 0\),然后写了两个 If ,然后就是大小样例双双寄掉。
后来,终于读对了,但是情况太多了,然后就漏了一些情况,还是没有分。在比赛中,我就往 \(\bmod\ 3\) 的方面去想,然后就没想成。然后,我就在想:要不要用大样例找规律?最后,确实是找出来一些不知道是真是假的规律。但是,还是不对。
正确的背包与我的背包只相差两步之遥,虽然这道题的暴力已经拿到,但对于 dp 的掌握及粗心的改正还有待加强。
B:武义寺(wuyi)
期望得分:\(30\),实际得分:\(30\)。
这种推式子数学题我接触较少。
一开始,我看到期望。吼,还好,我还学过一点点。答案不就是 \(\cfrac{\sum \text{val}(p)}{n!}\) 吗,那么 \(n!\) 能 \(O(n)\) 解决。但是 \(\sum \text{val}(p)\) 需要找规律,如果暴力的话时间复杂度是 \(O(n!)\) 的。然后打出了 \(n\) 为 \(1\) 至 \(6\) 的 \(\sum \text{val}(p)\)。但是还是没有找到规律。
正解是让人呕吐的推式子:
暴力可行方案为 \(k((k + 1)^{n - k} - k^{n - k})\)。
那么 \(\sum \text{val}(p)\) 为:
\(\sum_{k = 1}^n (n - k + 1) \cdot k((k + 1)^{n - k} - k^{n - k}) \cdot (k - 1)!\)
\(=\sum_{k = 1}^n (n - k + 1) \cdot (k + 1)^{n - k} - k^{n - k}) \cdot k!\)
像这种组合排列的题,我大抵都接触的较少了。所以,我略需强化我的数学 whk 实力。
C:依久依久(yijiu)
期望得分:\(10\),实际得分:\(10\)。
送出题人两个字:恶心。
第一眼看到题目,感觉眼花缭乱,所以就跳过了。后来,才读懂题意。赛事想打个暴力,把一个数从 \(f_{86}\) 开始分解,也就是从 \(\ge 10^{18}\) 的最小斐波那契数开始分解。然后最后异或起来即可。然后,便开始想优化了。一开始想的是用 upper_bound 来缩小范围。可是,这没什么用。
这道题的考点是递归+前缀和,我们可以处理前缀异或和 \(S(n) = \bigoplus_{i = 1}^n \text{val}(i)\),询问时计算 \(S(r) \oplus S(l)\) 即可。像这种题我已接触较多了,可我的脑子里这种思维含量较少。我需要较多的做这种题,多加训练。
D:补幺梨(pear)
期望得分:\([40, 50]\),实际得分:\(45\)。
dp 转换图论,难。
看到这么板的题目,感觉很简单。然后,就是一眼丁真数据范围,寄掉。如果是 dp 的话,很简单,直接转移 \(f_j = f_j | f_{j - a_i}\) 然后去最大值即可,便打了 dp。然后看着数据范围的突破点,\(m\) 比较大,但又不是很大。想了很久还是没想出来,然后暴力大草 \(45\) 分。
真的没有想到正解是 \(\texttt{Dijkstra}\),要把本来的 dp 思维转化为图论思维,离大谱。对于思维转化,还是比较弱的。
20240924 YLOI-R2
A:集合(set)
期望得分:\([70, 80]\),实际得分:\(60\)。原因:打表没打全。
考试时在想,居然 \(1 \le n \le 200\),那么就是 \(O(n^3)\),可不可以把每一次相乘的数拆成 \(3\) 个数相加呢?然后,就是没有做出来。然后,又有一个思路,统计每个数字出现了多少遍,结尾全乘起来。所以,就写了一个 dp 来统计。可是,dp 写挂了。出现了两个小错误,赛后才发现。然后,时间不够了,就打了暴力,打了 \(1 \sim 39\) 的表,就提交了。
正确的背包与我的背包只相差两步之遥,虽然这道题的暴力已经拿到,但对于 dp 的掌握及粗心的改正还有待加强。
B:出租(hire)
期望得分:\(0\),实际得分:\(0\)。
这道题一开始就没有太注意,磕完 T1 之后就去 T4 了,这个后面才开始做。一开始在想,可不可以用一个统计数组来实现 \(O(1)\) 转移,但是,这样可能会分不清 \(2 \sim (2 + 1)\) 和 \(3 \sim (3 + 1)\) 的租客了。后来,就开始想暴力,但这样太麻烦,就处理了一会。后来,写成了一堆烂泥,然后只好输出 \(m\) 个 YES。
这道题是一道线段树的题目。可以考虑总房间数 \(k(r - l + 1 + d)\) ,然后判断 \(k(r - l + 1)\) 与租客的差是否无解。
考试时很可惜,我没有想到线段树。这证明对题目的判断和思维能力不够强。像这种题,暴力应该是要拿到的,而本人缺没拿到,值得反思。
C:集合(block)
期望得分:\([0, 20]\),实际得分:\(0\)。原因:太弱了。
望着部分分表格中 “树均为随机生成”。我就在想,如果是随机生成的话,那么不满足 \(u, v\) 不同时存在于这个连通块中或 \(u, v\) 在这个连通块的概率很小(实际上不小)。再根据 \(m \le 20\)。所以应该可以把全图非负的全部加上,然后就挂了。
这一题巧妙地运用了图论。我本身就对图论的理解不是很强。这一题近似树状 dp,这种题我接触较少。
D:跳棋(checkers)
期望得分:\([0, 10]\),实际得分:\(0\)。原因:太弱了。
考试时望着一堆部分分,一眼就定住了全是 ? 的 Subtask,分比有些 Subtask 多且看起来有规律。
直接手动模拟+暴力求出 \(n\) 为 \(1 \sim 7\) 的数字,分别为 \(2, 4, 10, 26, \cdots\)。然后使用瞪眼法,还是没找到规律。
本题的考点为 dp。我们可以设 \(f_{i, j, k, 0/1}\) 为表示已经填了前 \(i\) 位,有 \(j\) 个 \(1\),\(k\) 个 \(0\),\(i\) 是否可以在后面接一个 \(1\) 变成 \(11\)。最后对于每种情况乘 \(C^{i + j}_i\)。实际上,可以把第一维压缩成 \(0/1\)。
这一次考试有两个 dp 题,都没能做出来,这说明薄弱点在于 dp,有待继续深造。
20240925 YLOI-R3
A:变幻(change)
期望得分:\(60\),实际得分:\(60\)。
写挂的贪心居然还有 \(60\) 分。
开始以为改了之后有后效性,所以就没有用可爱的 DP。然后就用了贪心,循环 \(k\) 次表示每次改动。每次改动取能改动的数改成低谷后的最大值,一个数需要满足本身不是低谷且两边的数都不是低谷该能改动。然后就是大样例寄掉,总少那么一点点。
正解其实是 DP,对于判断能力我还是都待加强。我们可以设计一个三维 DP \(f_{i, j, 0/1}\),其中第三维表示上一个位置是否被改变过,\(i\) 表示当前位置,\(j\) 表示之前已经变换过 \(j\) 次。
B:交替(alternate)
期望得分:\(40\),实际得分:\(40\)。
暴力,启动!
首先是打了表找了规律,大概是:
n = 1: a[1]
n = 2: a[1] + a[2]
n = 3: a[1] - a[3]
n = 4: a[1] - a[3] + a[2] - a[4]
n = 5: ......
......
找了一个小时还是没找出来,迫不得已暴力直接 \(40\) 分。
这道题确实是一道找规律的题目,这一题的关系在系数,可以发现系数与杨辉三角有关。对于简单的找规律题,本人还是能轻松做出来的。但如果稍微复杂一点就做不出来了,这说明对于找规律题还有待加强。
C:打拳(box)
期望得分:\(20\),实际得分:\(20\)。
全排列+分治+DP 大草 \(20\) 分。
题面看了很久才看懂。
看着 \(1 \le n \le 9\),\(1 \le m \le 16\),感觉很简单。可爱装压 DP?看着不像啊。然后定住了 \(k = 1\) 的
Subtask。然后也是失败了,就用全排列枚举,用分治维护谁赢,用 DP 来维护 LIS,成功 \(20\) 分。
这道题虽然较难,可是我还是把该拿的分拿到了,但不是很完美。也没有考虑完全装压 DP,最近的比赛有很多数学题,我都没能做出来,应该反思。
D:扑克(poker)
期望得分:\(0\),实际得分:\(0\)。原因:太弱了。
一看到扑克大模拟,没有太大希望。感觉情况很多,打 \(20\) 分代码。后来打着打着,就觉得情况太多了,同花顺、四条……都要考虑到。然后打出了一堆长长的代码,卡死了。就一直 Debug,最后还是放弃了
这道题严格上不算大模拟,但是还是得有一定的代码能力和思维能力。我们可以大模拟枚举所有五元组,然后再可能的情况下二分。我对于这种大模拟的码力还有待加强。
20240926 YLOI-R4
A:智乃的差分(difference)
期望得分:\([10, 30]\),实际得分:\(0\)。
原因:\(x = 0\) 写挂了。
直接开启大分讨,分别用 \(x > 0\),\(x = 0\),\(x < 0\) 来判断。 \(x > 0\) 直接倒序输出,\(x < 0\) 正序。但是,当处理到 \(x = 0\) 的时候,却卡住了。怎么判断 Yes,怎么判断 No。后来,想了很久才想出。然后,想出来的被轻松 Hack。哦吼,完蛋。我一直思考着,直到去了趟厕所,茅塞顿开。只需要判断相同的数是不是 \(\ge \lceil n \div 2 \rceil\) 即可。然后,就是漫长的 Debug。可是,这种情况非常复杂,调了 \(114514\) 年还没出来。我以为不判断 \(x = 0\) 有分,然后就是 0 pts 大挂。
知道比赛结束还没有搞明白这道题,后来看题解,还是没把 \(x = 0\) 的情况看懂。什么队列,map,看得我眼花缭乱。总结一句,对代码的处理有待加强。
B:牛牛的旅行(tour)
期望得分:\(0\),实际得分:\(0\)。
什么?如果 LCA 没 WA 可以拿 \(60\)???!!!
原因:LCA 写挂了。
嗯,一眼不会,直接打暴力。但是 \(n \le 1000\) 直接搜是 \(O(n^2(n + m)) = O(n^3)\) 的,需要用 \(\text{LCA}\) 优化成 \(O(n^2 \log n)\)。然后,漫长的 LCA,终于写完了。耶,样例输出 \(34\),错辣。检查了一下路径计算,\(\text{dep}_x + \text{dep}_y - 2 \cdot \text{dep}_{\text{LCA}(x, y)}\) 也没错啊,然后又打了个 \(10\%\) 数据的 \(\text{val}_i\) 值相等的乱搞,然后以为有 \(30\) 分。
题解中说 “如果学树分治或者树上 DP 学傻了可能往这两个方向去想就偏了”。这道题要把问题拆开,转换成求 \(\sum_{s \neq t} \text{happy}(s, t)\) 和 \(\sum _{s \neq t} \text{len}(s,t)\) 独立的两部分,分别求解。所以,做题不能太死板。
C:第 K 排列(permutation)
期望得分:\([5, 10]\),实际得分:\(20\)。
什么?输出 \(-1\) 可以得 \(20\) 分???
考试时一眼没看,觉得太难了,就先去做 T4 了。最后看这道恶心题,就输出了 \(-1\)。
考后看了题解,什么?\(\text{DAG}\) 图上 \(k\) 短路问题?哦,原来只需要把 \(k\) 短路转换成 \(O(nk)\) 的 DFS 利用动态规划进行剪枝就可以了。第一次比赛也出现了转图论问题,真的没有想到正解是 \(\text{DFS}\),要把本来的数学思维转化为图论思维,离大谱。
D:牛牛的 border(border)
期望得分:\(30\),实际得分:\(30\)。
叫我骗分大王!!!
一眼 KMP?假了!然后直接 \(1 \le N \le 3000\) 和仅有小写英文字母 a 组成直接启动。打暴力时出了点小问题,没有 reverse 。仅有小写英文字母 a 的公式为 \(\sum_{i = 1}^n \frac{i(i - 1)}{2} \cdot (n - i + 1)\)。然后获得 \(30\) 分佳绩。
这道题有一个新知识,后缀排序,我大抵都接触的很少了。这道题的思维能力很强,我需要加强。
20240929 YLOI-R5
A:光(light)
期望得分:\(70\),实际得分:\(70\)。
评价:中规中矩。
考试的时候觉得 \(\Theta(n^4)\) 拿的太少了,就思考 \(70\) pts 的 \(\Theta(n^3)\)。可以分别枚举左上、左下、右上(\(a, b, c\))的耗电。根据 \(a, b, c\) 分别的耗电和亮度,直接算出 \(d\)(右下)。我们把满足 \(a, b, c, d\) 达到要求至少所需的能量取 \(\max\) 作为 \(d\) 的耗电。计算答案时直接取 \(\min\) 即可。
没有想到这一题是伪整体二分,我以为是枚举两个 for 循环直接计算。没有想到这题整体具有单调性。这一题整体偏贪心,但又不算贪心。对于这种题目,思维性比较强。
B:爬(climb)
期望得分:\(10\),实际得分:\(10\)。
考试时一眼树形 dp,没想出来。然后打了 \(10\) 分暴力,枚举每个蚂蚁是否跳到父亲节点,然后统计每个的节点有多少蚂蚁,计算即可。
这道题的考点是二进制,我们可以考虑每个位置每个二进制位对答案的贡献。在考试时,如果遇到这种题,我们可以考虑状压 dp 或根据二进制的性质来解决问题。平常,我对二进制的题接触较少,所以不是特别熟悉。对于装压 dp,我大抵都已忘记了,所以觉得还得去 oi-wiki 学习一下二进制。
C:字符串(string)
期望得分:\(20\),实际得分:\(20\)。
考试时打了 \(20\) 分暴力。直接枚举当前位置是填 \(\text{A}\) 还是 \(\text{B}\),然后边填边计算,最后取 \(\text{max}%\) 即可。
考后看了题解,才知道我们可以对字符串进行简单分析,用贪心的思想来思考怎样设计才能使得权值最大。其实这道题的思路不难理解,我们可以枚举 \(\text{A}\) 和 \(\text{B}\) 切换了多少次,然后考虑 \(\text{A}\),再考虑 \(\text{B}\)。然后经过计算,就可以得出答案。
D:奇怪的函数(function)
When \(1 \le n \le 10^5\),\(1 \le q \le 3 \times 10^5\),\(\mathcal{O}(nq) = \Theta(\frac{1}{80}nq)\)。——Holzky Gould (Eng)
当 \(1 \le n \le 10^5\),\(1 \le q \le 3 \times 10^5\) 时,\(\mathcal{O}(nq) = \Theta(\frac{1}{80}nq)\)。——霍尔兹基·高德 [英]
期望得分:\(5\),实际得分:\(75\)。牛逼!!!!
出题人因为卡正解,出了卡正解 \(\Theta(\log n)\) 处理 \(\max, \min\) 值的数据。导致暴力直接退化成大约 \(\Theta(\frac{1}{80}nq)\) 级别,直接卡过(除全是的询问的特殊情况)。考试的时候看到暴力只有 \(5\) 分,没有报太多希望。然后看特殊性质,每一个会的都没有,然后就成功打了暴力。
这一题的正解是线段树,线段树处理最大最小的模板忘记了,就没有打正解,回去回炉重造线段树。再一个是,这道题还需要用到分段函数,这个东西需要一定的数学能力,我还需要加强我的数学。
20240930 YLOI-R6
A:博弈(game)
期望得分:\(0\),实际得分:\(0\)。
太难辣!!!!!
考试的时候一开始准备用 \(\Theta(n^2(n + m)) = \Theta(n^3)%\) 的方法做。先枚举点对 \((u, v)\),然后用 \(\Theta(n + m)\) 的 Dfs 来求出 \(S\) 数组,然后再判断先手是否有必胜策略即可。但是,部分分 \(1 \le n \le 5000\),就算写了也是 \(0\) 分大挂。
这道题的知识点是 \(\text{Xor-Hashing}\),我之前没有接触过。看了题解的博文我才知道,这是一项要掌握的技术。主要出现在使用 \(\text{XOR}\) 时,我们计算每个元素的出现次数是偶数还是奇数,而不是实际出现次数。像这种我还没有接触的技术,我觉得应该学习学习。
B:跳跃(jump)
期望得分:\(20\),实际得分:\(20\)。
DP 已经把我绕晕。
考试的时候一眼可爱 \(\text{DP}\),虽然考试时想的是二维,用 \(f_{i, 0/1} = v\) 表示在 \(i\) 位置,是向左还是向右,\(v\) 表最大分数。然后就是想不出来,就打了 \(20\) 分暴力。枚举当前点可以往哪跳,然后直接搜索。
考试的时候想假了,我们可以令 \(f_i\) 保存从 \(1\) 跳到 \(i\) (下一步应该是以 \(i\) 为右端点的区间,进行一个反复横跳)所需要的最少次数,和跳到 \(i\) 以后的分数。近期的 DP 题我都没有想出来,说明我的 DP 还需要加强。
C:大陆(mainland)
期望得分:\(0\),实际得分:\(0\)。
最近怎么这么喜欢考树?
考试时也是成功的把问题转换成:构造 \(1 \le k \le n\) 个节点集合(大小位于 \(B\) 与 \(3 \times B\) 之间),使得每个集合要不是一个连通块,要不然可以通过加上一个点变成一个连通块。然后就在想,是不是可以把树划分成若干个连通块?嗯,不会。然后直接跳过。
对于数据结构,我还是有待加强。最近的考试中,树出现的较频繁,而我也是都没有想出来。这道题代码其实很简单,可以用 DFS + 栈来实现。
D:排列(permutation)
期望得分:\(40\),实际得分:\(40\)。
最近怎么这么喜欢考树?线段树、平衡树……
考试一眼觉得是线段树或者平衡树,不会。然后看到暴力居然有 \(40\) 分,感觉比其他题实惠。右移 \(k\) 次其实就是把后面 \(k\) 个数给他直接倒序放在前面来。然后我们可以做一个 \(\Theta(n^2)\) 的 dp 来维护序列的 LIS。只要 \(\max f_i\) 大于等于了 \(3\),就一定存在三元上升子序列。为什么呢?你看,最大的上升子序列长度都 \(< 3\),难道还有其他的 \(\ge 3\) 的吗?
题解看不懂,平衡树只会模板。
20241002 YLOI-R7
由于 CCF 在 \(2022\) 年发射的 “CSP-Senior” 宇宙射线通过一年一个省份的速度到了湖南长沙,并把今天的模拟赛的数据破坏了,导致 T1 和 T2 数据出锅。
躲避技能(skill)
期望得分:\(40\),实际得分:\(20\)。
数据出锅了,居然没有单独 \(1 \le m \le 10\) 的数据,LCA 是 \(\mathcal{O}(n \log n + m \log m + m! \cdot m \log n)\) 的,是可以过掉 \(40\) 分的。结果数据只有 \(n, m\) 都 \(\le 10\) 的,啊……
考试时一看,\(w_i\) 为什么要倒着给出。欧,原来 \(1 \le w_i \le 10^{100}\),方便高精度运算。啊?高精度,直接放弃正解。线性的 \(1 \le n, m \le 10^5\) 不会,直接考虑 \(40\) 分解法。直接 LCA \(\Theta(n \log n)\) 预处理,然后就可以 \(\Theta(\log n)\) 算距离:\(\text{Dis}(x, y) = \text{dis}_x + \text{dis}_y - 2 \cdot \text{dis}_{\text{LCA}(x, y)}\)。有了 LCA 开挂,我们就可以愉快的枚举 \(m\) 个账号的全排列(next_permutation),然后枚举 \(m\) 个账号。对于每个账号,直接计算 \(\sum_{i = 1}^n \text{Dis}(s_i, t_i)\),最后取每个的 \(\min\) 值就可以解决问题了。
这一场比赛又双叒叕考了可爱的树。这一题还要高精度,我大抵已经忘记了。所以回去还得回炉重造一下高精度,让自己二次复习。这一题的解法需要用到贪心,而贪心又需要较强的思维能力。主要的思路可以从这句话体现:对于每一棵子树,先跟子树内的起点和终点匹配,匹配不了的再到子树外去匹配。
但是,这里主要的丢分点在脚客牛客的数据,居然没有让 LCA 过的数据,pty 还说不如写 \(80\) 分的 \(1 \le n, m \le 10^5\)。这属于一种歧视 LCA 的行为,严重批评。
奶茶兑换券(tea)
期望得分:\([0, 5]\),实际得分:\(0\)。骗的大样例。
赛时看题,感觉题目很抽象。第一眼感觉跑背包,但是 \(1 \le n \le 10^5\),\(1 \le a_i \le 10^9\),直接寄掉。然后看部分分,但也只是 \(n\) 的范围减小了,也不行。问题可以转换成:把奶茶分成若干个组,使得浪费最少。但如果这样理解的话,这道题会变成 DP。居然转移方程和状态都想不出来,就去看 T3 了,后来看这题直接骗了大样例。
虽然这道题没有想出来正确解法,但我觉得骗不到分非常不应该,暴力也没有想出来。这道题的贪心思路不是那么难,也还是让人觉得不难理解。算法是双指针,主要就是要双指针来匹配,让所有 \(> \frac{m}{2}\) 的奶茶从大到小匹配。于是。这道题完美转换成了匹配问题,可以完美解决。
帮助(help)
期望得分:\(30\),实际得分:\(30\)。
一开始看到这题,就在想:像这种题,一定是要转换的。于是我思考了图、树……等等数据结构,甚至想到 \(\texttt{Dijkstra}\) 了。还感觉这题可以用区间来理解并解决,只不过没有想到正解的扫描线。没办法,扫描线不是很精通啊,打 \(1 \le n \le 1000\) 的暴力。暴力的主要思路就是枚举 \(i\) 和 \(j\) 两个人,看是否 \(i\) 愿意帮助 \(j\),且 \(j\) 接受 \(i\) 的帮助。如果可以,\(j\) 加上 \(i\) 做的题目数。注意,这里要判断自己帮助自己,因为 \(i\) 也可能满足自己的要求,所以必须特判。时间复杂度 \(\Theta(n^2)\),可以拿 \(30\) 分。虽然这还可以用树状数组来维护,但是用了等于没有用,还是提不了分数。
这道题有很多部分分,可以我只骗到了暴力,其他的一点都没有骗到。这道题的解法是扫描线。对于扫描线,我之间是接触过一点的。扫描线基于线段树,它一般被用来解决图形面积,周长,以及二维数点等问题,而且能有效地解决区间问题。主要就是以扫描每个区间。我与满分擦肩而过,实在很可惜。这道题其实还可以用树状数组加上离散化做,主要思路就是递推。用 \(s\) 数组表示表示所有成绩为 \(j\) 且愿意帮助成绩为 \(i\) 的人,所做题目数量之和,然后推出每个人受到帮助后的题目数量。
神奇的变换(change)
期望得分:\(20\),实际得分:\(20\)。
被 T4 硬控半小时。
题面过于冗长,也挺幼稚。主要就是把一个数列进行分解质因数、因数和、因数个数,还强制在线。一看到这种题,一定是数据结构。首先我就猜到了分块,没想到猜对了。但是,想到了有什么意义,反正也写不出来。直接写 \(\Theta(nq\sqrt{\prod_{i = l}^r a_i})\) 的暴力,用前缀积优化。可过 \(n = 1\),\(q = 1\) 的数据,可获 \(20\) 分。但是,样例错了,一直不知道哪里错了,直接红温肘击电脑。后来发现只是答案输出错位,看来 Debug 能力有待加强。
我在考试中骗的分数不满意,没有想到 \(\prod_{i = l}^r a_i \le 10^7\) 的情况下,可以用质数筛来筛出来。序列直接做前缀积,逆元就可以了。但是,我猜对了,这道题的正解就是分块。但是,分块我还是学的不精通,只会一点点。pty 说这道题有三个点:在线、区间、分解质因数。像这种题,一般是要发现一些数学性质,用这些性质来做出这道题。比如说,这道题有一个性质:序列中的每一个数字,最多只 “包含” 一个大于 \(1000\) 的质数。发现了关键点后,我们就可以来仔细分析题目,然后解决。
20241003 YLOI-R8
总和(sum)
期望得分:\(100\),实际得分:\(100\)。Easy!
这道数学题还是很简单的,首先知道填的方法有 \(m^n\) 种。然后,对于序列 \([a_1, a_2, \cdots, a_n]\),重复情况只有当 \(k\) 为 \(1\) 至 \(m\) 的时候,才会与 \(a_i + k\) 同余(\(\bmod\ m\))。所以重复的有 \(m\) 种,那么答案为 \(m^{n - 1}\)。
这道题巧妙地运用了数学思维,通过推理得出答案的题型很多。但是,这题 AC 不代表我能 AC 所有的这种题型的题目,还得举一反三。顺便说一下,从 R1 以来只 AC 了这一道。
水果加工(fruit)
期望得分:\(40\),实际得分:\(40\)。
题面过于冗长……考试时看到这道题,这题面是给人读的吗。然后经过我若干时间的精密分析,题面终于理解了。就是有 \(n\) 个果园,要送往 \(2\) 个加工厂,然后给定运输成本,果园机器数,以及一堆东西,要把水果用机器加工,让你算合法完成水果加工所需要的最小时间是多少。
题解说过掉 \(5 \sim 8\) 测试点要写 \(\Theta(b^2 \sum a_i)\) 的背包,但我写的 DFS 就这么水灵灵的荣获 \(40\) 分了?万能的暴搜 DFS,枚举每个点分别给两个基地分配多少水果,加上一点奇怪的剪枝,比如果 \(b_0 < c_{0, i}\) 且 \(b_1 < c_{1, i}\),那就直接 return 。分配完之后就用公式计算,然后答案取 \(\min\)。时间复杂度大概 \(\mathcal{O}((a_i)^n)\)。最近是原来越会骗分了,也会打一些优质暴力。话说 DFS 还是挺万能的,啥都能解决。
最佳位置(location)
期望得分:\(20\),实际得分:\(0\)。
不知道为什么暴力挂了。
题面简洁,好评。暴力的思路:第一个人直接坐 \(1\),第二个人直接坐 \(n\)。对于其他人,枚举 \(n\) 个座位。如果是空座位,枚举与其他非空座位的距离,然后取距离 \(\min\)。最后,取最大的距离 \(\min\) 值的座位坐。样例过了,不知道什么挂了。都来把距离修改成数组,\(\text{dis}_i\) 表示座位 \(\min\) 值,就直接过了。时间复杂度 \(\Theta(mn^2)\)。
这道题的正解是 STL 大合集,直接放弃了。
跑步(run)
期望得分:\(60\),实际得分:\(75\)。
Linux 牛逼!
使用 LCA 大法,首先用并查集跑最小生成树,然后连边之后把 LCA 初始化。初始化完后输入 \(k\) 个点,利用公式 \(\text{dis}_x + \text{dis}_y - 2 \cdot \text{dis}_{\text{LCA}(x, y)} + (\text{dep}_x + \text{dep}_y - 2 \cdot \text{dep}_{\text{LCA}(x, y)}) \cdot \text{t0}\) 来算出从上一个点到这一个点花费。这里要特判一下,如果上一个点与这个点相同,那么不计算,因为重复。然后,以为能拿高分,结果才 \(75\)。一看,把 LCA 里面的 \(\log n\) 看成 \(60\),所以空间复杂度 \(\Theta(n \log n) = \Theta(60n)\),加上其他直接爆,还开了 long long。
虽然时间复杂度还是 \(\Theta(m \log m + k \log n)\),但是空间直接爆掉了。主要失误是在 LCA,而且没有算时间复杂度。离正解就差一步之遥,实在太可惜了。奉劝大家 CSP 的时候算算复杂度再打好代码,真的是血的教训。
20241006 YLOI-R9
喷泉(fountain)
期望得分:\(100\),实际得分:\(0\)。
继上次的 T4 MLE 事件,这一次又是 Shadow y1 事件。真的非常难受,答辩 VS Code 没有识别出 y1 是库函数,就直接给我屏蔽掉了,没报错。吼?关键是,我居然还没有发现,然后就快快乐乐的提交了。考完交补题,编译错误?然后成功发现偷偷藏在代码里的 Shadow y1,然后寄掉。虽然 Lemon 上评测成功了(windows),但不算最终成绩!然后 Shadow Linux 直接给我报错,直接 \(175 - 100 = 75\) 分到手!\(C_n^m\)。pty 说赛前已经强调过了,变量不能建 y1,所以不能改代码。这东西跟开头那就搞一道几何 T1 帮助大家爆零成功呼应,坑点是这东西,实在是没想到。
回归解法。我们通过图 1 理解。先来探讨 \(r = 0\) 时鸡尾酒在躲狗的时候的最远距离。首先,我们肯定知道,鸡尾酒肯定要离 \(\text{D}\) 点最远,也就是从 \(\text{C}\) 点到线段的距离尽可能长。那么,鸡尾酒只可能往 \(\text{A}\) 或 \(\text{B}\) 点方向走。而鸡尾酒又要尽可能远,那么只能远到 \(\text{A}\) 点或 \(\text{B}\) 点,显然答案就是 \(\max(\text{AC}, \text{BC})\)。那如果 \(r > 0\) 怎么办?我们看图 2,小狗在躲避时肯定不会到 \(\text{Q}\) 点。而是绕到与 \(\text{B}\) 点最远的 \(\text{E}\) 点,使得距离变为 \(\text{BC} + r\)。所以说,答案为 \(\text{AB}\) 两端与点 \(\text{C}\) 的距离加上半径 \(r\) 的 \(\max\) 值。
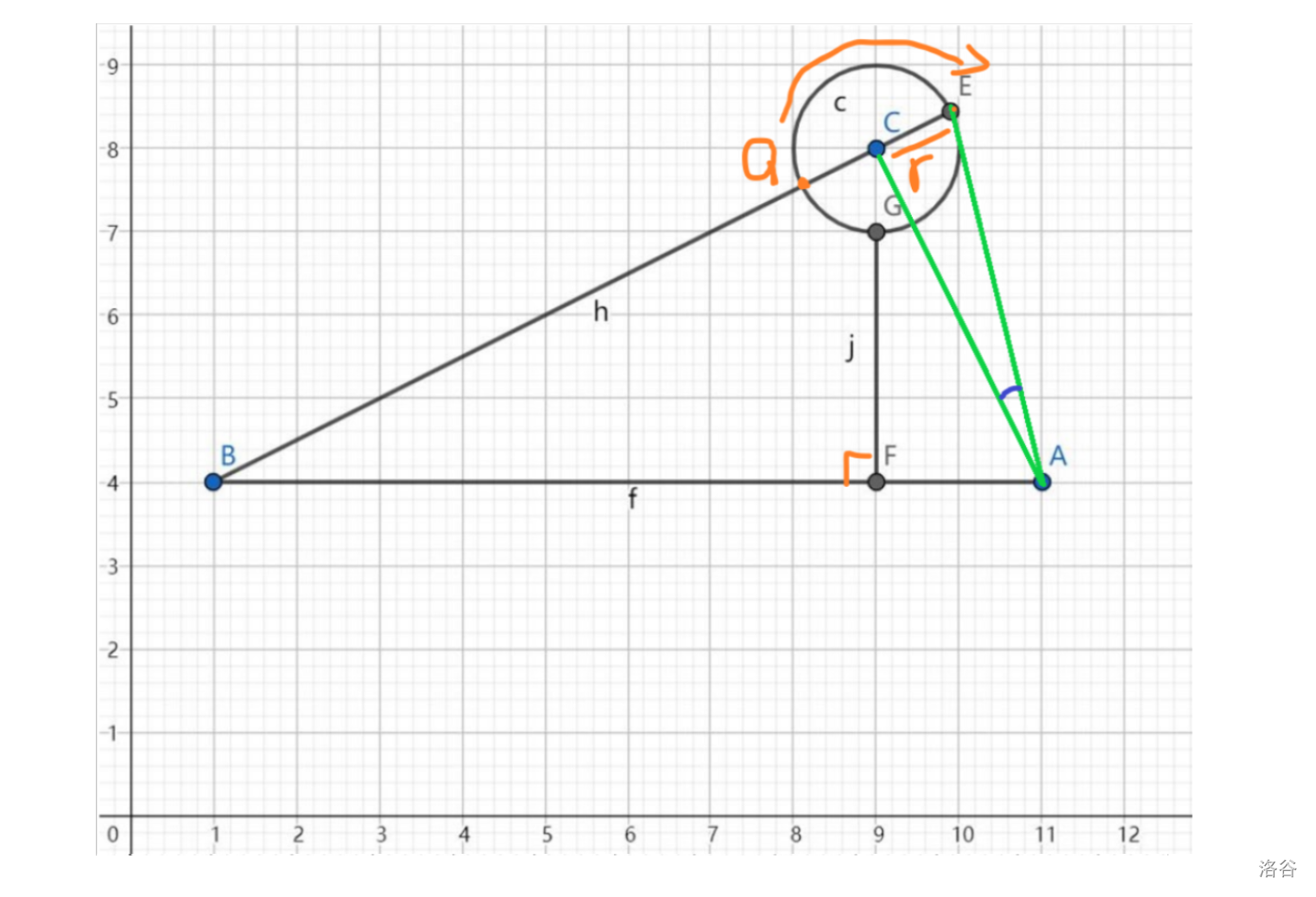
然后探讨 \(r = 0\) 的最短距离,我们把两人的家 \(\text{AB}\) 和喷泉中心 \(\text{C}\) 连起来成一个三角形,然后根据欧拉公式 \(\text{Dis}(x_1, y_1, x_2, y_2) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}\) 来算出 \(\text{AB, BC, CA}\) 的距离。然后根据海伦公式 \(p = \frac{1}{2}(a + b + c)\),\(\text{S}_{\triangle\text{ABC}} = \sqrt{p(p - a)(p - b)(p - c)}\)。显而易见,最短距离肯定是三角形的高 \(h\),我们知道 \(\cfrac{1}{2}ah = \text{S}\),那么 \(h = \cfrac{2\text{S}}{a}\)。所以答案为 \(\cfrac{2\text{S}}{a}\)。那 \(r > 0\)?显然,图 2 小狗会呆在最近的 \(\text{C}\) 点,而不会外绕其他点,所以减去 \(r\) 即可。所以答案为 \(\cfrac{2\text{S}}{a} - r\)。最后记得保留二位小数。
图 1:
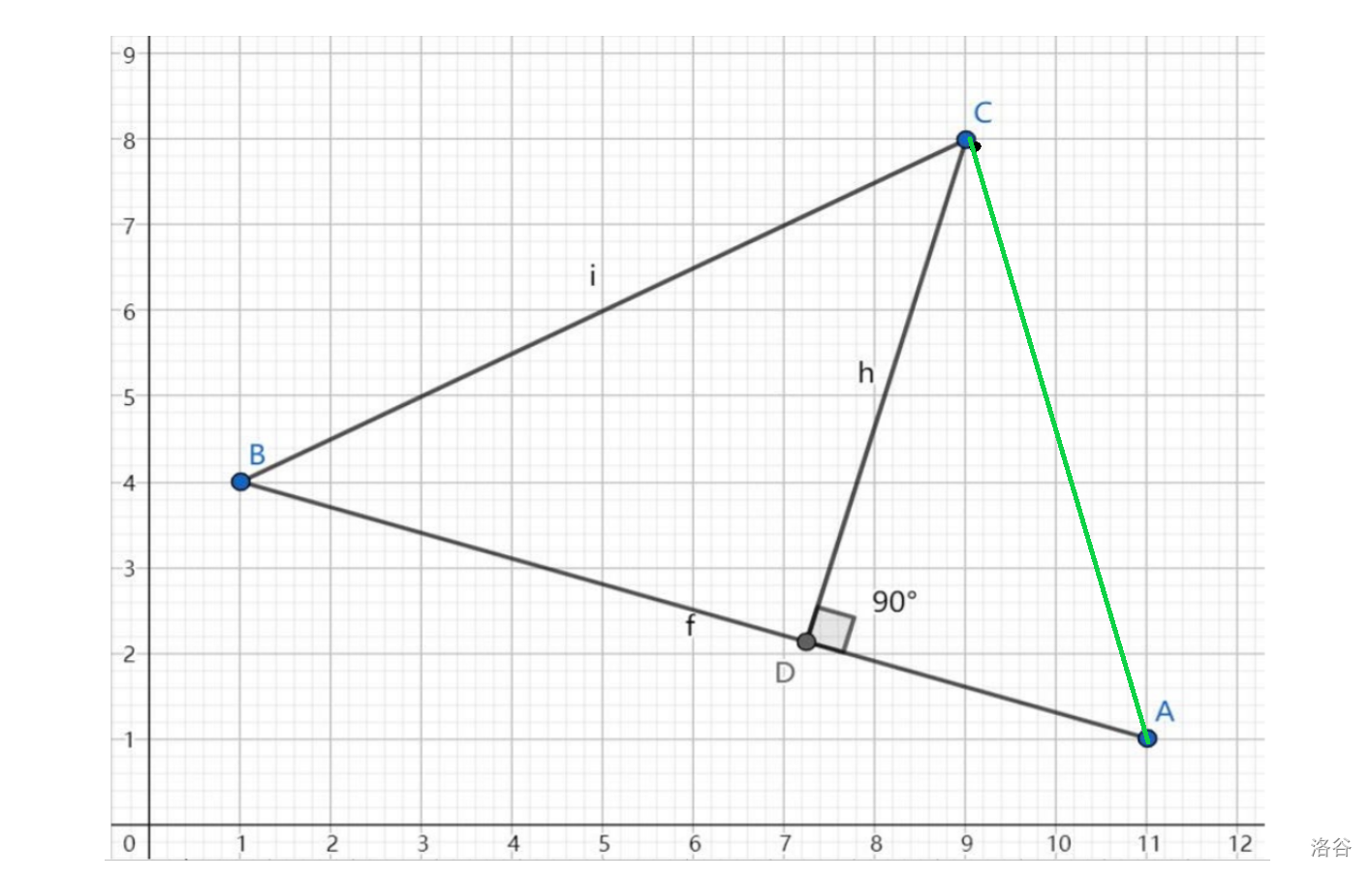
图 2:
红绿灯(light)
期望得分:\([70, 100]\),实际得分:\(70\)。
第一个点 TLE?欧,没有特判 \(m = 0\)。
一眼定准 \(\Theta(nm)\) 暴力 \(50\) 分,枚举 \(1 \sim n\) 的时刻,然后枚举 \(m\) 个红绿灯。判断当前时刻 \(t\) 是否为 \(a_i\) 的倍数,如果不是,那就增加到 \(a_i\) 的倍数。也就是把 \(t\) 增加到 \(a_i - (t \bmod a_i)\),但当 \(a_i\ |\ t\) 时,不需要进行操作。然后就是看到了 \(a_i\) 为 \(2, 3\) 的循环的 \(20\) 分,用暴力找规律。规律是:当 \(m \ge 4\) 时,答案就是从 \(6\) 开始一直输出,每隔 \(6\) 个数把输出的数 \(+6\)。当 \(m < 4\) 时,交给 \(\Theta(nm)\) 暴力。
写完 \(70\) 分解法之后,突然开窍。当通过第 \(1\) 个红绿灯时,\(1 \sim a_i\) 时刻出发的都会在时刻 \(a_i\) 到达第 \(2\) 个红绿灯,\(a_i \sim 2 \cdot a_i\) 时刻的会在时刻 \(2 \cdot a_i\) 到达,\((2 \cdot a_i + 1) \sim 3 \cdot a_i\) 时刻的会在时刻 \(3 \cdot a_i\) 到达,以此类推。而接下来红绿灯的也是同理,根据到达时刻来分组。例如,当 \(n = 10\),\(m = 3\),\(a = [2, 4, 3]\),分组如下(① 表示第一个灯,圈表示一个组):
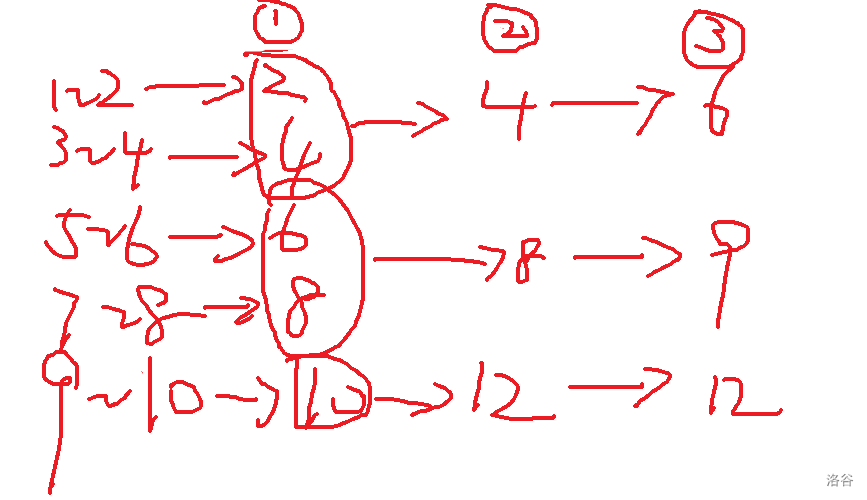
如此下去先分治把组数压缩,再展开,就得到答案。但是实现麻烦,所以只压缩了第一个红绿灯的分组,直接枚举每个组,在组内随便选一个初始时刻计算到达时间即可。时间复杂度为 \(\Theta(\frac{n}{a_1} \cdot m)\),当数据的 \(\text{limit}\)(也就是 \(a_i\) 随机范围)足够大时,可以 AC。然后可能数据较强,只能卡到 \(80\) 分。但是,我没有特判 \(m = 0\),导致 i += a[1] 死循环,直接寄掉 \(10\) 分,变成 \(70\)。
具体实现如下:
for (int i = 1; i <= n; i += a[1]) {
ll ans = i + a[1] - 1; // 初始时刻,这里取组内初始时刻最大值
计算到达时间...
for (int j = i; j <= min(n, ll(i + a[1] - 1)); ++ j) {
cout << ans << ' ';
}
}
集合(subset)
期望得分:\(10\),实际得分:\(5\)。
为啥?
题面公式较为抽象,什么 \(x ∈ S\) 的抽象东西。花了好久才看懂,还是得借助样例。看到 \(1 \le k \le 10^9\),觉得肯定是 \(k\) 次方或者乘上 \(k\),反正不是大于 \(\log\) 级别的。然后觉得这一定有一个递推式。然后没想出来。选择了 \(k = 1\) 且 \(1 \le n, m \le 10\) 的部分分。主要思路就是枚举 \(S\) 的子集,判断这个子集和是否 \(= m\)。如果是的,答案 \(+1\)。特判 \(m = 0\),直接输出 \(1\),因为只有空集是符合要求的。时间复杂度 \(\Theta(n! \cdot n)\)。然后思考 \(a_i = 1\) 的部分分,没有找到规律。然后不知道为什么,挂到了 \(5\) 分,没有取模?不是。
还是太菜了,没有接触过太多关于集合的东西。也不是很理解集合的思想。回去多学学集合,为 CSP 打下基础。我需要注意编程细节,加强数学和算法思维,以及扩展知识面。
佛怒火莲(fire)
期望得分:\([0, 30]\),实际得分:\(0\)。骗的大样例。
第一眼看到 \(2 \le k \le 5\),直觉 \(2^k\) 状压 DP。但是,不知道怎么设计状态。然后就看到了 \(1 \le n \le 100\) 的数据点,直接搜索。枚举每一个火焰要选哪个,如果这个属性的火焰之前没选过,那么就选。但是,我的暴力的时间复杂度是 \(\Theta(n^k)\) 的,于题解说的 \(\Theta(C_n^5)\) 完全不同。测了大样例,最后一组变强卡过,但是输出 \(0\)。然后直接偏离样例,惨痛离场,至今也不知道为什么。
不知道为什么爆掉,以后得好好检查代码,增强 Debug 能力。正解如我所愿,是状压,我对状压的状态设计还不是太熟练。回去要多多练习状压 DP,多做题。
20241007 YLOI-R10
R10 大庆!
通过了 R1~R9 的历练,今天终于迎来了 R10 大庆。比赛进入了高潮,今天的题格外难,两题都考了期望,我接触的很少。另外两题也比较难,一道还要数形结合,难。而且本场的暴力分也比较难拿,需要一定思维。
我是 A 题(A)
期望得分:\(30\),实际得分:\(40\)。
这得分,啊?
花了 \(2\) 个小时。一开始一直在想:删除不大于 \((u, v, w)\) 的相当于删除了 \(u \times v \times w\) 个,但是怎么去重?然后看到 “请选手仔细观察给出的数据生成器,数据生成方式与解题强相关”。吼?那就开始 ”仔细观察”。观察到发现在随机 \(u, v, w\) 之后有三个小 if,发现有 \(\frac{1}{3}\) 的概率 \(u = A\),还有 \(\frac{1}{3}\) 的概率 \(v = B\),如果都没有,那么 \(w = C\)。也就是说,\(u, v, w\) 总有一个为极值。有了这个性质,题目就简单多了。
我尝试的把样例的 \(u, v, w\) 输出出来,发现满足 \(u = A\) 且 \(v = B\) 的操作很多,甚至有三个都是极值的。然后经过我的探索,发现只要当 \(n\) 足够大,\(A, B, C\) 较小时,输出 \(A \times B \times C\) 有 \(90\%\) 以上的概率可以通过。更详细地说,当 \(n\) 与 \(\max(A, B, C)\) 的比值 \(\ge [100, 1000]\) 时,答案有很大的概率为 \(A \times B \times C\),因为生成出这种情况的平均概率为 \(\frac{1}{3} \times \frac{1}{3} \times \frac{1}{C} \times n = \frac{n}{9C}\)。这个结论足以通过测试点 \(3 \sim 6\) 和 \(14 \sim 15\)(开始时以为只能通过 \(3 \sim 6\))。较小的测试点 \(1 \sim 2\) 交给 \(\Theta(n \times A \times B \times C)\) 暴力。
做完这些,我有继续思考正解。当时想,其实每个操作都可以分成两类,第一种为 \(u = A\) 且 \(v = B\),其他统一为第二类,输出答案为两类相加。第一类只需要统计 \(w\) 的 \(\max\) 值,答案即为 \(A \times B \times \max w\)。而第二类维护较难,需要对 \((u, v, w)\) 去重。首先考虑了第三维,如果 \(w\) 小于等于第一类的 \(\max w\),不做计算。因为这样的话已经被第一类计算过了,读者可自证。但是,花了很久时间也没想出怎么去重,交了 \(40\) 分代码。其实数据比较水才导致我可以通过 \(14 \sim 15\),那个测试点的 \(n\) 与 \(\max(A, B, C)\) 的比值才达到 \(10\),理论上通过概率较小。
虽然我的暴力骗分能力有进步,但还是不够好,今天的暴力两题都没有骗到手。还是很菜,的提升一点骗分能力,为 CSP 打下基础。
我是 B 题(B)
期望得分:\(0\),实际得分:\(0\)。
第一次见负概率。
考试时看见题目,期望?又接触到了准知识盲区(还是接触了一点,懂概念)。然后看到有 \(1 - p_i\) 的概率通过,什么?负概率我还是真没有见过。然后就开始推理,每个东西到能成功活下来的概率为:\(-\cfrac{1}{|\prod_{i = 1}^n (p_i - 1)|}\),然后把 \(n\) 个物品组合出的概率再组合一下就为期望。但是,我怎么想都没有想出来,期望的分母应该怎么求,就放弃了。然后暴力不会打,直接大样例启动。
正解是熟悉的概率 DP,概率 DP 是我接触最少的 DP,只做过一题。我觉得从现在开始,应该把概率 DP 快速选一下,下次碰到期望就可以不那么困难了。
我是 C 题(C)
期望得分:\(35\),实际得分:\(45\)。不是?
题目比较简洁,易理解。感觉有点像滑动窗口,但是想不出来。直接打暴力,倒序枚举 \(k\),每次遍历数组中长度为 \(k\) 的窗口。统计窗口内的每个数字,如果每个数字出现次数都 \(\ge k\),直接输出 \(k\),因为 \(k\) 是从大到小枚举。时间复杂度 \(\Theta(n^3)\),跑不满。然后又看见了 \(b\) 全部相等的 \(20\) 分。有大概率可以输出 \(0\),因为 \(b_i\) 在随机数据下比 \(a\) 所有数出现的次数都大的概率比较大。所以,如果 \(1 \le n \le 300\),打暴力,否则就输出 \(0\)。但没想到数据这么水。
这道题的正解是分治。主要是没有考虑到 \(b\) 有单调性,因为 \(b\) 是单调下降的,所以 \(k\) 越大要求的出现次数就越多。一个数字 \(x\) 导致一个区间不可行,那么这个区间所有包含 \(x\) 的子区间必然也不可行。虽然这道题的暴力分我拿到了,但是我觉得我太蠢了。因为我的暴力思路本来可以写 \(\Theta(n^2)\) 的,可以我就是写了 \(\Theta(n^3)\)。就是枚举左端点,然后滑动窗口,不断扩大长度,一边扩大一边统计出现次数。最后取符合要求的窗口长度的 \(\max\) 值。
我是 D 题(D)
期望得分:\(0\),实际得分:\(0\)。难!
考试时根本不理解极长相等子段是什么意思,猜测是最长的每个元素都相等的字段。然后读着读着,期望?又是期望?因为不理解什么意思,就没有思考,胡乱输出了 \(n^2\)。
看来题解的转换,我才恍然大悟。哪一坨屎就相当于满足 \(x_i = x_{i + 1} = \cdots = x_j\) 的数对 \((i, j)\) 的数量。有了这个转换,我们就只需要算出,满足 \(x_i = x_{i + 1} = \cdots = x_j\) 的概率和就可以了。这道题可以用线段树维护,在 \(\Theta(n \log n)\) 内完美解决。
20241009 YLOI-R11
今天的大样例前面的 ex 按照平常来说是大样例的意思,然后这次是题目名。(此处应有配乐, \(↗\) \(↘\) \(\rightarrow\rightarrow\rightarrow↗↗\rightarrow\rightarrow\rightarrow\)……)。
矩阵交换(change)
期望得分:\(100\),实际得分:\(0\)。绝望。
继上次的 Shadow y1 事件,这一次又是 Shadow ex 事件。考试的写完代码后看到大样例写的 exchange1.in,就以为 ex 是大样例的意思,然后就建了名为 change 的文件夹,名为 change 的程序……然后当我自信的提交吃完饭回来后,看到评测机上面的题目名是 exchange 就崩溃了。然后就是 \(100 \rightarrow 0\)。
我的思路比较直接。可以按行排序,因为我们要保证每一列单调不减,所以在排序时按照第一个不相等的元素从小到大排序。排序后检查一遍数组的每列是不是单调不降序列即可。这样做其实是为了尽量保证面的数是从不降的,同时这也可以保证有解时后面的数字可以排序成功,因为题目中是一行为整体。不会出现输出无解但是有解的情况。举个反例,比如说,像这种:
\(\begin{bmatrix} 3 & 1 & 2 \\ 1 & 2 & 3 \end{bmatrix}\)
排序后是这样的:
\(\begin{bmatrix} 1 & 2 & 3 \\ 3 & 1 & 2 \end{bmatrix}\)
后面的单调不降了,但是前面的乱了。但是,像这种矩阵不管是什么形态,都无解(可自证)。前面说了题目中是一行为整体,我们也是按行排序,所以各种无解情况在排序的时候就一定会体现出来了。
代码实现很简单,可按行开结构体。时间复杂度 \(\Theta(T \cdot nm \log n)\),排序中比较函数是 \(\Theta(m)\) 的。
砖块摆放(trick)
期望得分:\(40\),实际得分:\(20\)。绝望。
感觉想哪里见过一样,原题吧?
考试时看到这道题,总感觉它有一些异或的性质。比如说 \(x \oplus x = x\),\(x \oplus y = (x + y) \bmod z\)。然后看了看大样例,发现输出一定是 \(\text{A, B, C}\) 中的一种,不会产生另外的颜色。突然,想到了可以把 \(\text{A, B, C}\) 转换为数字或者二进制来解决此问题,因为 \(\text{A, B, C}\) 有 \(3\) 种颜色,所以就想到了是不是可以用 \(3\) 为主体的运算来得到上一个颜色。但是估计我的眼睛不够大,瞪眼法没练够,没搞出来。
然后就是打了 \(\Theta(n^2)\) 暴力。枚举 \(n - 1\) 次,模拟摆放,然后根据题意模拟出上一层砖块,然后把上一层砖块拿来做上一层来推导上上层的颜色。但是,\(20\) 分远远不能满足我。所以就打了接下来二十分,字符串仅包含两种字符且交替出现。很简单,往上推第二层,全部都是另一种颜色,如:
\(\text{\ \ A\ \ \ A\ \ \ A\ \ \ A\ \ \ A}\)
\(\text{B\ \ \ C\ \ \ B\ \ \ C\ \ \ B\ \ \ C}\)
然后,如果相邻两个是相同,那么上一层相同。所以,砖块就会一直相同下去,直到到达顶峰。所以,答案即为最后一层没有的那一个颜色的砖块,\(\Theta(1)\) 完美解决。但是没搞懂这 \(20\) 分为什么错,欧,原来是这种错误(直接挂掉了):
if (s[0] == 'A' && s[1] == 'B') {
ans[0] = 'C';
} else if (s[0] == 'A' && s[1] == 'C') {
ans[0] = 'B';
}
......
打完后,看一下在下一个 \(20\) 分的,感觉没什么规律,跳过。
这道题的整解我已经理解,就是把 \(\text{A, B, C}\) 转换成 \(0, 1, 2\),假设这一层相邻的两个砖块的颜色为 \(x, y\),那么上一层的颜色为 \(-(x + y) \bmod 3\)。然后根据观察,顶层的值的系数跟杨辉三角一样。如 \(n = 5\) 时,顶层的颜色为 \((x_1 + 4x_2 + 6x_3 + 4x_4 + x_5) \bmod 3\)。然后还要判断正负。时间复杂度 \(\Theta(n \log_3 n)\)。这道题虽然理论上我的暴力分拿到了,但是我觉得我还是缺乏这种数学思维,准确来说找规律思维还没有完全训练好。我觉得应该多做做这种题提升,这种情况已经出现过很多次了,但是就是有点懒,还是得提拔一下。
学习 LIS(lis)
期望得分:\(10\),实际得分:\(10\)。绝望。
看到了题目 \(1 \le n \le 20\),要不超级剪枝搜索,要不 \(2^n\) 状压 DP。但是状压太难了,不会,暴力启动。我们可以暴力来搜每一个数,选择可能得值,也就是 \([1, m]\)。当 \(m\) 个数全部分配完之后跑一个 \(\Theta(n^2)\) 的最长上升子序列(LIS,转移方程 \(f_j = \max(f_j, f_i + 1)\))。时间复杂度 \(\Theta(n^m)\)。但是,我明明可以在搜索的过程中就做好每个元素的 LIS,在分配值的时候就开始检查并且可行性剪枝。如果这第 \(i\) 个元素分配到值 \(x\) 时 \(\mathcal{O}(n)\) 检查 \(\text{lis}_i\),如果不符合直接剪枝。虽然时间复杂度最坏 \(\mathcal{O}(m^n)\),但是可以卡过 \(1 \le n, m \le 10\) 的数据。
问题主要体现于状压 dp 能力较弱,看来目前状压 DP 还没有复习完全。
战略轰炸(bomb)
期望得分:\(0\),实际得分:\(0\)。绝望。
感觉题目非常不清晰,一开始感觉是道不可做题。后来才想到,暴力 \(4\) 分感觉太不起眼,考虑了特殊性质 A。然后发现做不出来,拜拜。
这种不会的题一句话:菜,就多练。
20241010 YLOI-R12 总结
收集植物(collect)
期望得分:\(0\),实际得分:\(10\)。嗯?
考试第一眼看到这道题,感觉题面比较模糊,就直接跳过写 T2 了。后来回来看这道题才把题意看懂,然后就开始思考,怎么购置植物使得最优?难道把价格 \(\le k\) 的全部买了,无法达到最优。然后就想到了每个购置的于下一个购置的会形成一个区间,如 \([3, 2, 5, 4, 1, 6]\) 购置 \(2, 1\),那么会形成两个区间,\([5, 4]\) 和 \([6, 3]\),那么可以通过购置的来变出这个区间内的植株。我考虑到了枚举购置 \(k\) 棵植株,然后购买 \(k\) 棵价格最小的植株,用这些植株来变出剩下的植株,每次用标记来判断那些植株是有的。时间复杂度 \(\Theta(n^2)\)。
可是,这显然是一个错误的解法。所以,就直接打 \(\Theta(n^n)\) 的 \(20\) 分暴力。枚举每个植株买还是不买,然后枚举完后来运算需要多少次才能使得全部的植株都有(跟题解不同)。但是,由于没有计算变换植株时原来的植株所需要的花费,所以 WA 掉。后来因为时间不够,直接输出 \(\sum_{i = 1}^n a_i\),居然还有 \(10\) 分,因为有个数据点 \(k\) 很大,\(a_i\) 很小。
这道题的正解是二分+ST/三分+单调队列/倍增。我还真没有看出 \(k\) 可以表示为一个单峰函数,可以直接三分,就连这道题有倍增做法都觉得奇怪。这道题的暴力分居然没拿到,很不应该。还是缺乏思维,虽然底子是有的,但是拔高不够。
美丽子区间(interval)
期望得分:\(40\),实际得分:\(40\)。
看到这道题,第一眼感觉是 RMQ,但是没有猜到是单调栈(话说 ST 表的时间复杂度好像比单调栈跟优啊)。但是就算维护了区间,也不会轻易知道区间最大最小值的位置。好吧,没办法,想不到容斥,暴力吧。
这一次差点又上当了。一开始想的是枚举区间左端点和有右端点 \(i, j\)。然后 \(\mathcal{O}(n)\) 求出这个区间的最小最大值,奇怪的是,我还想着 \(\Theta(n \log n)\) 的排序。然后求出来后对比位置,检查即可。但是,这 \(\Theta(n^3)\) 东西是给没有脑子的人的,实在可以 \(\Theta(n^2)\) 啊。用 \(\Theta(n)\) 来枚举左端点,然后向右滑动窗口,一边滑动一边来更新最小最大值,把位置要记录下来。每滑动一次检查一次位置,如符合要求答案 \(+1\)。
要脑子的暴力分拿到了,比较满足。这道题需要容斥来解决,具体就是把总区间数减去不符合要求的区间就可以了,具体的,优美区间的数量为:总区间数 - 最大值在开头/结尾的子区间数量 - 最小值在开头/结尾的子区间数量。但是,这样子的话最小值和最大值同时在开头或结尾会算两次,所以答案加上最大值在开头且最小值在结尾的子区间数量 + 最大值在开头且最小值在结尾的子区间数量。
字符序列(subseq)
期望得分:\(20\),实际得分:\(20\)。
首先不是普通的字符串肯定必有蹊跷,然后就发现了题解中 \(T_i = T_{i+1} + c_i + T_{i+1}\) 的公式(但有略微不同)。然后根据字符串拼接的性质,旧字符串的每个字串肯定会跟新添加的字符串组合起来变成新的字串。这不就是典型 DP,但是不知道状态怎么设计啊(况且这题还要矩阵乘法)。然后直接暴力,首先枚举出 \(s_n\),然后暴力搜索字串,拼接起来用一个 map 统计,没统计过的答案 \(+1\),记得取模。
这道题需要把 DP 的思维转换成矩阵乘法的思维,要把每一种字符对应一种转移矩阵。这种转换题我还是接触的太少了,听完讲解后要举一反三,多做一些类似的题,好继续巩固这方面的弱点。
网络攻防(attack)
期望得分:\(0\),实际得分:\(0\)。
嗯?\(k\) 非常小,直接暴力跑他减(Tarjan),但是 Tarjan 去年学的,只能凭记忆力来回忆,回忆不上来。然后就想到了枚举炸哪条边,然后枚举任一点对,暴力遍历是否可以通达,时间复杂度 \(\Theta(m^k \cdot n(n + m))\),可以获得 \(5\) 分的好成绩。那么,输出随机数。
这一题的正解看不懂,只能回去学一下随机类的这种奇怪算法。这道题输出 \(0\) 可以得 \(10\) 分,我居然没想到。