目标检测 | Spatially Sparse Convolution
Spatially Sparse Convolution
导言
为什么需要稀疏化?
在3D表示中,除了点云(Point Cloud)和网格模型(Mesh),我们常常还会使用到一种称为体素(Voxel)的表示方式。类似于像素(Pixel),这种表示方式将空间均匀地切割为一个个方块,TSDF和占据网格(Occupancy Network)都可以视为体素的一种变形。
最朴素的体素表示方式,这是一种稠密(Dense)的表示形式,我们给定一个\(L\times W\times H\)的包围盒,体素尺寸为\(1\times 1\times 1\),那么我们将得到一个\(L\times W\times H\)的\(bool\)矩阵:
那么假设我们有一个\(70.4m\times80m\times4m\)的室外点云场景(KITTI点云格式的感知范围),给定每个体素大小为\(0.16m\times0.16m\times4m\)(PointPillar将点云体素化的参数),那么将得到一个大小为\(440\times 500\times1=220,000\)的体素网格,而最终有效的体素数量不会超过\(40,000\)个,即利用率不会超过\(18\%\),稠密表示形式下,有\(80\%\)的存储空间是被浪费的。
我们在模拟器中简单采集一帧点云做个实验就可以看到,当体素大小为\(0.05m\)时,基本保留原始点云的细节,但此时占用率不足千分之一。
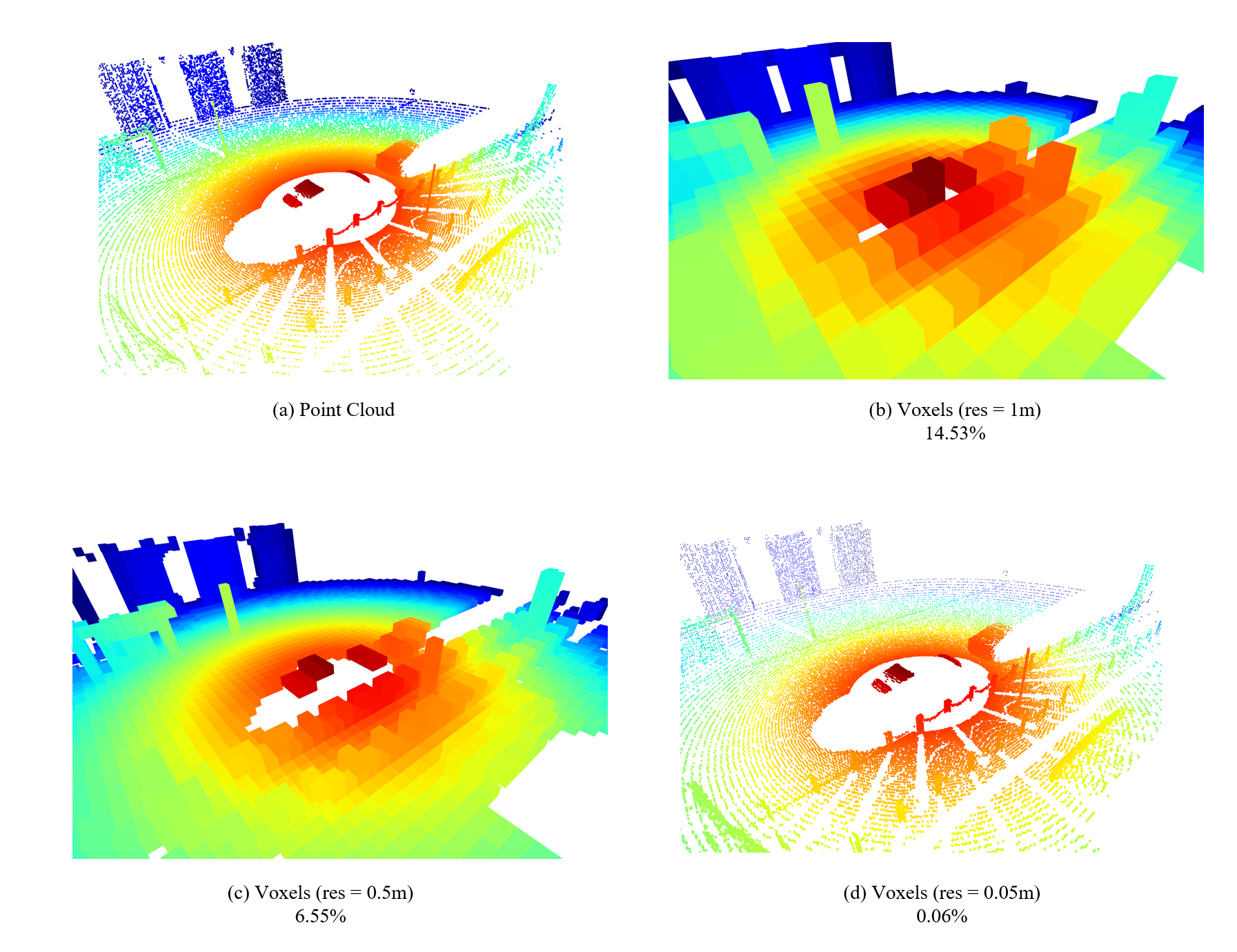
所以只表示有效体素的稀疏化表示就这样提出了,这种表示有效降低了内存的冗余,并加速了对体素的处理。
稀疏卷积
最常用的稀疏卷积分为Spatially Sparse Convolution(SparseConv)和Submanifold Sparse Convolution(SubMConv),前者是常规卷积操作的稀疏化版本,后者是保证不破坏特征图稀疏度的卷积操作。
现代通用版本的SparseConv实现出自于SECOND: Sparsely Embedded Convolutional Detection
SubMConv出自于3D Semantic Segmentation with Submanifold Sparse Convolutional Networks
稀疏卷积主要分为三个步骤:
- 张量稀疏化
- 建立Rulebook链接
- 特征收集计算
稀疏卷积
张量稀疏化
张量稀疏化就是顾名思义将一个张量从稠密表示形式变换为稀疏表示形式,我们给出常用的COO内存的定义,给定一个张量\(\mathbf X\in \mathbf{R}^{N_1\times N_2\times\cdots \times N_m}\)与稀疏维度\(d\ge1\),得到一个索引\(\mathbf{I}\in\mathbf{R}^{n\times d}\)以及值\(\mathbf{V}\in\mathbf{R}^{n\times N_{d+1}\times\cdots \times N_m}\),其中\(n\ge 0\)为张量中的非\(0\)量的数量
比如:
- 给定\(\mathbf X\in\mathbf{R}^{2\times 2} = \text{[[0, 2.], [3, 0]]}\),\(d=2\),得到\(\mathbf I\in{2\times 2} =\text{[[0, 1], [1, 0]]}\)以及\(\mathbf{V}\in\mathbf{R}^{2}=\text{[2., 3.]}\)
- 给定\(\mathbf X\in\mathbf{R}^{2\times 2\times 2} = \text{[[[0., 0], [1., 2.]], [[0., 0], [3., 4.]]]}\),\(d=2\),得到\(\mathbf I\in{2\times 2} =\text{[[0, 1], [1, 1]]}\)以及\(\mathbf{V}\in\mathbf{R}^{2\times2}=\text{[[1., 2.],[3., 4.]]}\)
五种内存管理形式
- COO, CSR, CSC, BSR, and BSC.