matlab学习2(数据预处理、简单(非)线性规划、多目标规划)
1.matlab导入数据
注意事项:记得保存数据,清空工作区或者关闭matlab后数值就没有了。
2.数据预处理
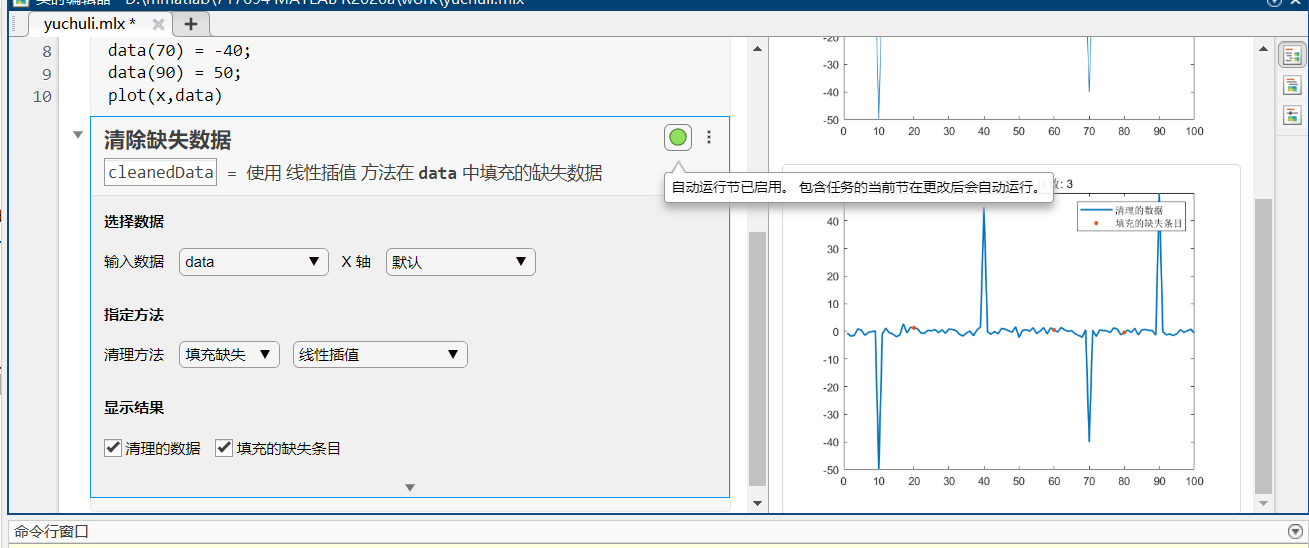
清理缺失值
实时编辑器-->任务-->清理缺失数据
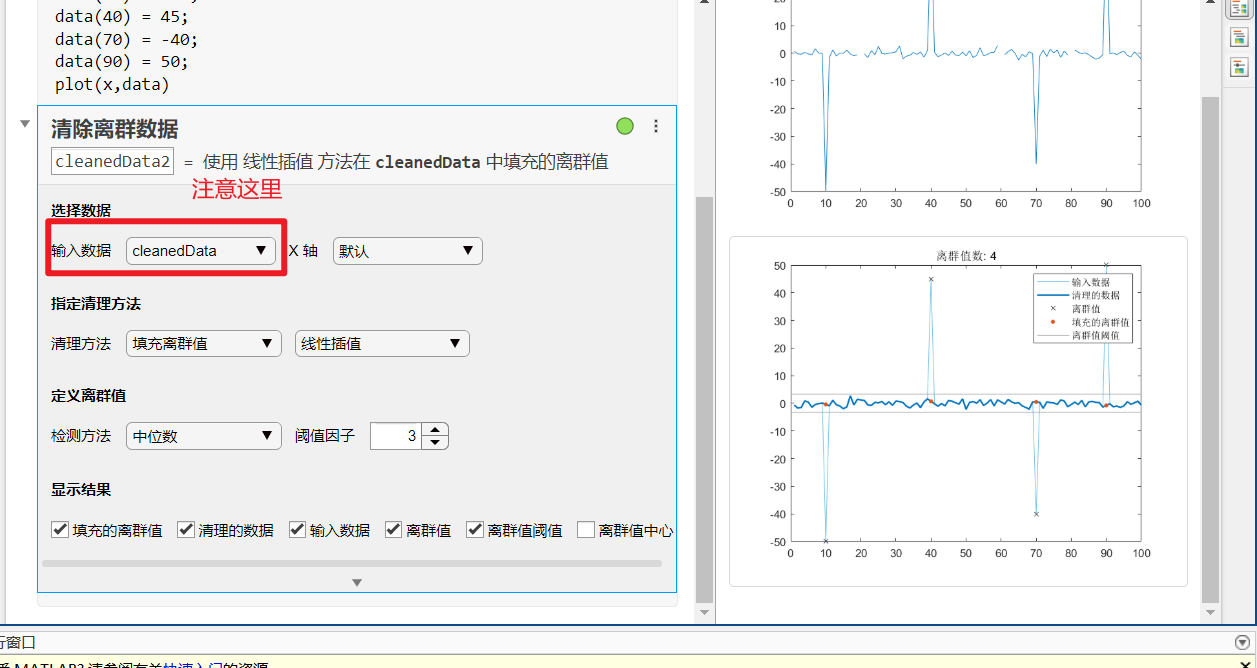
处理异常值:
实时编辑器-->任务-->清理离群数据
例子:
x = 1:100; %构造一个数组,元素为1,2,...,100 % randn(1,100) 生成1行100列矩阵 data = randn(1,100); data(20:20:80) = NaN; %设置第20,40,60,80个元素缺失值 % 设置4个异常数据,正常数据在0附近 data(10) = -50; data(40) = 45; data(70) = -40; data(90) = 50; plot(x,data)
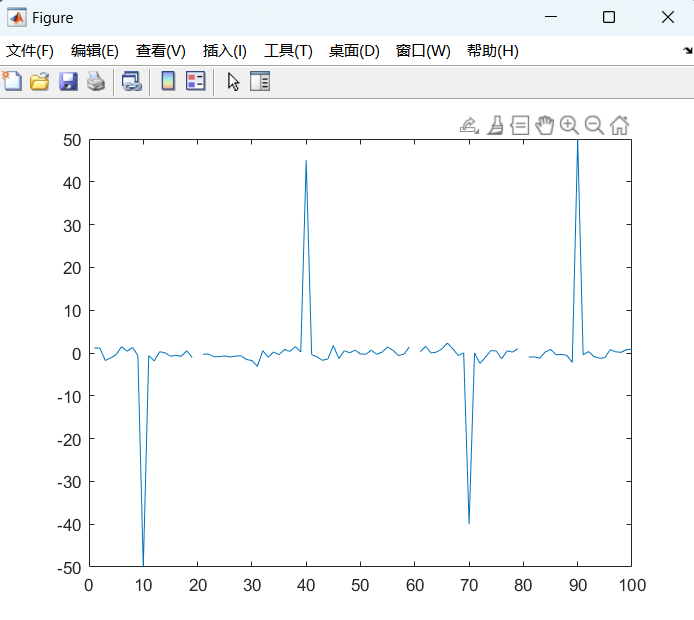
3.简单线性规划
线性规划就是在一组线性约束条件下,求线性目标函数的最大或者最小值
线性意味着所有变量都是一次方的
Linprog函数使用条件:
需要模型化为matlab标准型:目标函数求最小值,约束条件小于对于号或者是等于号
f:目标函数的系数列向量
A,b:不等式约束条件的变量系数矩阵和常数项矩阵
Aeq, beq:等式约束的系数矩阵和常数项矩阵
lb, ub:决策变量的最小取值和最大取值
[x,fval] = linprog(f,A,b,Aeq,beq,lb,ub)
其中x返回最优解的变量取值,fval返回目标函数的最优值
注意:
如果不存在不等式约束,用 []代替A和b
如果不存在等式约束,用 [] 代替Aeq和beq
如果没有等式约束和最小和最大值的约束时,可以不用写Aeq、beq和lb、ub
如果题目求的时最大值,目标函数两端加负号转求最小值,记得求解后的目标值需要再取负
例子:
max y = 40x1 + 30x2
s.t. x1 + x2 ≤ 6
x1 ≥ 1, x2 ≥ 1
240x1 + 120x2 ≤ 1200
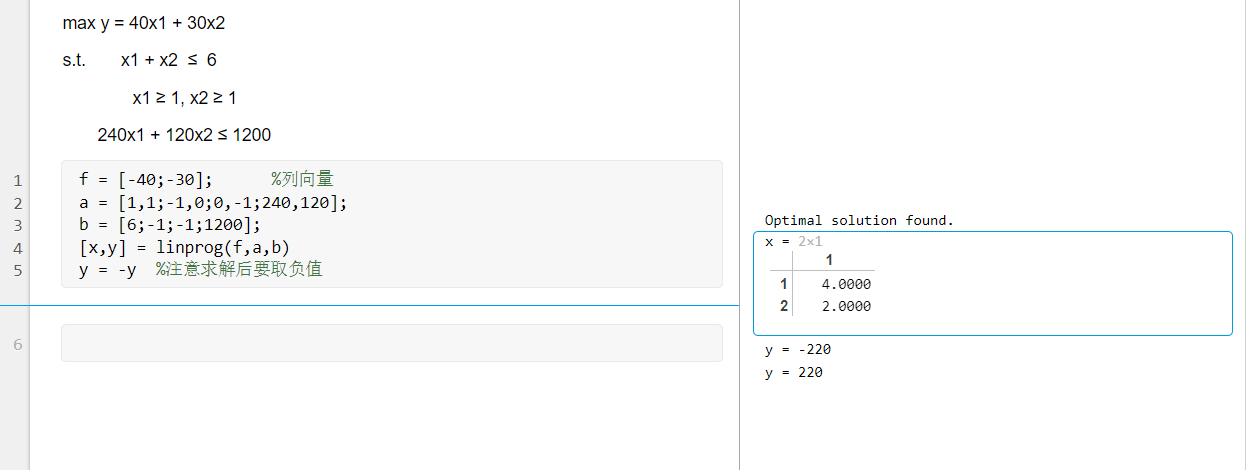
4.简单非线性规划
非线性规划:至少有一个变量不是一次方的
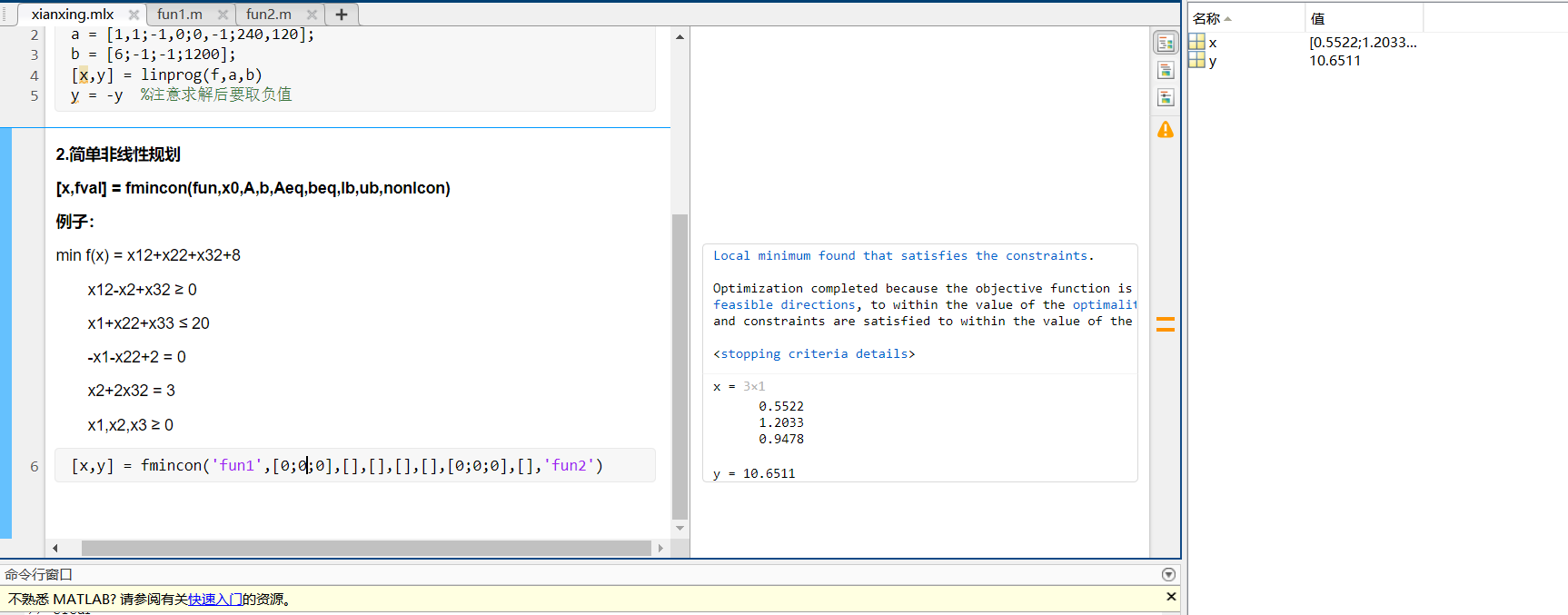
[x,fval] = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)
其中x是得到的决策变量取值,fval得到的是最优解取值
fun:单独函数文件里定义的目标函数
x0:决策变量的初始值,这个可以随便写,求出来的结果都一样
A,b:线性约束不等式变量系数矩阵和常数项矩阵
Aeq,beq:线性约束的等式变量系数矩阵和常数项矩阵
lb,ub:决策变量的最小取值和最大取值
nonlcon:非线性约束,包括不等式和等式
例子:
min f(x) = x12+x22+x32+8
x12-x2+x32 ≥ 0
x1+x22+x33 ≤ 20
-x1-x22+2 = 0
x2+2x32 = 3
x1,x2,x3 ≥ 0
fun1.m文件
% 目标函数fun1;目标函数为f(x)=x12+x22+x32+8 %这里会给x1、x2、x3,通过这个sum(x.^2)变成x12+x22+x32 最后再加上8 function f = fun1(x) f = sum(x.^2)+8;
fun2.m文件
% 非线性约束 function [g,h] = fun2(x) % g是非线性不等式 g=[-x(1)^2+x(2)-x(3)^2 %原本函数中是x1^2-x2+x3^2 大于等于 0 x(1)+x(2)^2+x(3)^2-20]; %原本是x1+x2^2+x3^2 小于等于 20,20要移过去左边 % h是fei线性不等式 h=[-x(1)-x(2)^2+2 x(2)+2*x(3)^2-3];
5.多目标规划
(非)线性规划都是只有一个目标函数
要衡量每个目标的完成情况,并主观上区分三个目标的重要性,使得整体的完成情况尽量好
三个只要概念:
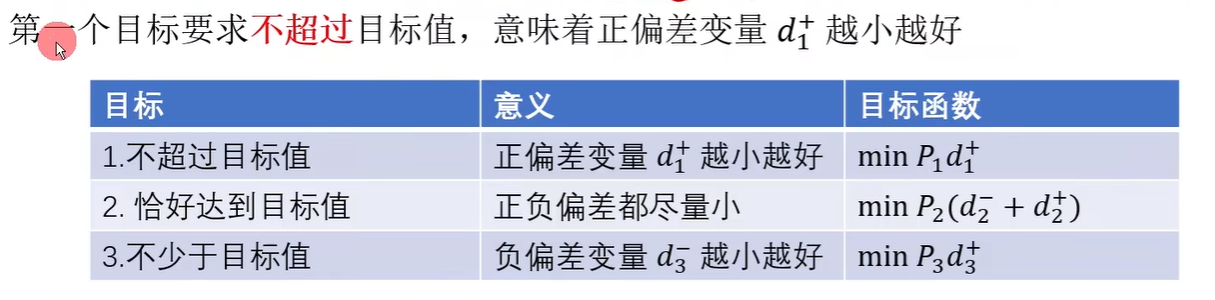
1.正负偏差变量
尽量不少于-->说明负偏差变量 d3- 越小越好
2.绝对约束和目标约束
绝对约束是模型中自带的约束条件,是必须要满足的条件,否则是不可行解
目标约束是模型中对不等式右端追求的值允许有偏差,例如一个不等式 8x1+10x2>=56,可以让他减去一个变量使其等于56。 8x1+10x2+di--di+=56
利用了允许偏差即正负偏差变量,多退少补,把目标函数变成等式约束条件。
3.优先因子
例如三个目标,给第三个目标优先因子为10,第二个目标优先因子为5,第1个目标优先因子为1,这三个目标的重要性之比就是10:5:1
例如 :
某工厂生产产品1,2,有关数据如下,