五一 NOI 数学听课笔记

RB16B / 2023-05-03 / 原文

注：本文不写证明。

https://www.wolframalpha.com/

花絮：真·sigma：，真·abc：，

一、剩余类环 $\mathbb{Z}/n\mathbb{Z}$

记号：$\overline{x}$ 在$\mod n$ 意义下代表一个集合：$\{\dots,x-2n,x-n,x,x+n,x+2n,\dots\}$

加法逆元：$a: \overline{-a} \text{ or }\overline{n-a}$

乘法逆元：$\overline{a}\times \overline{b} = 1$

费马小定理

\[a^{p-1}=1(\bmod p, 0 < a < p) \]

Euler's Theorem / 费马小定理推广：

\[a^{\varphi(p)}=1(\bmod p) \]

Quiz

计算: $3^{\left(3^{100}\right)} \bmod 100$。

使用 Euler's Theorem 需要算出 $\varphi$，计算得 $\varphi(100)=40,\varphi(40)=16$。

$\displaystyle 3^{\left(3^{100}\right)} \bmod 100=3^{3^{100} \bmod 40}=3^{3^{100 \bmod 16}}=3^{81}=3^{1}=3$

$\varphi$ 函数

Lemma 1：若 $n \bmod p = 0$，则 $\varphi(pn)=p\varphi(n)$。

Lemma 2：若 $n \bmod p \neq 0$，则 $\varphi(pn) = (p - 1)\varphi(n)$。

定理：若 $n = \displaystyle \prod_{i = 1}^{m} {p_i ^ {r_i}}$，则 $\varphi(n) = n \times \displaystyle \prod_{i=1}^{m}\left(1-\frac{1}{p_i}\right)$。

Example

$\varphi(60) = \varphi(4) \times \varphi(3) \times \varphi(5) = 2 \times 2 \times 4=16$。

HW1：

\[\sum_{d | n}\varphi(d) = n \]

二、扩展 Euclid

此算法可以计算形如 $ax+by=\gcd(a,b)$ 的解，递归求解。

记 $x_0, y_0$ 为：

\[bx_0 + (a \bmod b) y_0 = \gcd (a, b) \]

方程的解，所以

\[bx_0 + \left(a - \left\lfloor\frac{a}{b}\right\rfloor b\right)y_0 = \gcd(a,b) \]

整理得到：

\[x_1 = y_0, y_1 = x_0 - \left\lfloor\frac{a}{b}\right\rfloor y_0 \]

所以 $(x_1, y_1)$ 就是一组特解，通解为：

\[x=x_1 +k\frac{b}{\gcd(a,b)},y = y_1 - k\frac{a}{\gcd(a,b)}, k \in \mathbb{Z} \]

三、原根

对于正整数 $n$，集合 $G=\{\overline{x}:\gcd(x,n)=1\}$ 在乘法下为循环群，且 $G = <\overline {g}>$，那么 $g$ 就是一个在 $\bmod n$ 意义下的原根。

另一个说法：

\[\{\overline{g}, \overline{g}^2, \dots, \overline{g}^{|G|-1}\} = G \]

i.e. 在 $\bmod n$ 意义下的加法存在一个元素 $1$ 使得其他元素都是它的若干倍，我们希望在乘法意义下也找到一个这样的数，为了方便我们找到这样的数，会将所有的与 $n$ 不互质的数排除在外。

结论：$\bmod n$ 意义下存在原根当且仅当 $n = 2, 4, p^{\alpha}, 2p^{\alpha}$，其中 $p$ 为奇素数。

在 $\bmod n$ 意义下的原根数量是 $\varphi(\varphi(n))$。

Problem

给定 $n$，求 $n$ 的一个原根。

考虑随机化，单次的成功率是 $\displaystyle \frac{\varphi(\varphi(n))}{n}$，所以期望步数为 $\dfrac{n}{\varphi(\varphi(n))}$。

原根判定定理：设 $n \geq 3, \gcd(a, n) = 1$，则 $a$ 是模 $n$ 下的原根的充要条件是，对于 $\varphi(n)$ 的每个质因子 $p$，都有 $a^{\frac{\varphi(n)}{p}} \neq 1 (\bmod n)$

指标

定义：记 $g$ 为 $\bmod m$ 下的原根，对 $\gcd(a,m) = 1$ 的 $a$，若 $a = g^u$ 则记 $I(a) = u$ 称为 $a$ 的指标。

\[I(ab) \equiv I(a) + I(b), I(a^k) \equiv kI(a) \]

这也被称为离散对数。

BSGS, Baby Step Giant Step 算法

令 $L = \sqrt{\varphi (m)}$，预处理 $X = \{g^{L}, g^{2L}, \dots, g^{L^2}\}$ 和 $Y = \{g, g^2, \dots, g^{L - 1}\}$，容易发现一定存在 $x \in X, y \in Y$ 使得 $a = xy$。

那么我们枚举 $x$，查找 $y = x^{-1} a$ 是否在 $Y$ 中即可。

Extend BSGS 算法

给定 $b,a$，求一个满足 $a^u = b (\bmod p)$ 的 $u$。

注意：$\gcd(a,b)$ 不一定为 $1$，$p$ 也不一定是质数。

若 $b \bmod \gcd(a, p) \neq 0$ 且 $b \neq 1$，那么无解。

对于：

\[a ^ u \equiv b (\bmod p), g = \gcd(a, p) \]

两边同时除以 $g$：

\[a ^ {u - 1} \times \frac{a}{g} \equiv \frac{b}{g} \left(\bmod \frac{p}{g}\right) \]

然后换元：

\[a' = \frac{a}{g}, b' = \frac{b}{g}, p' = \frac{p}{g} \]

得到：

\[a^{u - 1} \times a' \equiv b'(\bmod p') \]

这样一直迭代下去，直到无解或者可以使用 BSGS 解决。

最终的式子变成：

\[m = \prod_{i = 1}^{k} g_i \]

\[a^{x - k} \times \frac{a^k}{m} \equiv \frac{b}{m} \left(\bmod \frac{p}{m}\right) \]

此时 $\gcd\left(\frac{a^k}{m}, \frac{p}{m}\right) = 1$，跑一遍 BSGS 即可。

二次剩余

求 $x^2 = n (\bmod p)$ 是否有解，若有求出一组。

结论：设 $n=g^u$，若 $u \bmod 2 = 0$，则 $x = g^{u/2}$ 就是一组合法解，否则无解。

三次剩余

继续推广：$p$ 为质数，求解三次剩余问题 $x^3 = a (\bmod p)$。

若 $p = 3k + 1, a = g^u$，则 $a$ 存在三次剩余当且仅当 $u \bmod 3 = 0$。

更一般的，若 $p = sk + 1, a = g^u$ 则 $a$ 存在 $s$ 次剩余当且仅当 $u \bmod s = 0$。

若 $p = 3k + 2$，$a \equiv a^{6k + 3} \equiv (a^{2k + 1})^3$。

一般二次同余式

\[ax^2 + bx + c \equiv 0 (\bmod p) \]

求根公式：$\displaystyle x = \frac{-b ± \sqrt{b ^ 2 - 4ac}}{2a}$

配方：$(x - \alpha) ^ 2 \equiv \beta (\bmod p)$

四、中国剩余定理

已知 $x \equiv a (\bmod p), x \equiv b (\bmod q)$。

其中 $\gcd(p, q) = 1$，求 $x \equiv ? (\bmod pq)$。

\[x = a + k_1p = b + k_2q \to k_1p + k_2q = b - a \]

当 $a = b$ 时 $x \equiv a (\bmod pq)$，当 $a \neq b$ 时，先解 $k_1p + k_2q = 1$，再将特解乘上 $b - a$。

五、数论函数

定义 $1.$ 若一个函数定义域为正整数，那么称这是一个数论函数。

定义 $2.$ 若一个数论函数 $f(n)$ 有 $f(ab) = f(a)f(b), \forall a, b \in \mathbb{Z}^{+}$，则称其为完全积性函数，若该性质只对 $\gcd(a,b)=1$ 成立则称其为积性函数。

结论：$\displaystyle \sigma(n) = \sum_{d | n} d, \sigma_k(n) = \sum_{d | n}d^k$ 都是积性函数。

Mobius 函数

定义：

\[\displaystyle \mu(n) = \begin{cases}1, n = 1\\0, p^2 | n\\(-1)^r, n = \displaystyle \prod_{i=1}^{r}p_i\end{cases} \]

Dirichlet 卷积

定义：令 $f, g$ 为两数论函数，定义：

\[f * g (n) = \sum_{d | n} f (d) g \left(\frac{n}{d}\right) \]

称 $f * g$ 为 $f$ 和 $g$ 的 Dirichlet 卷积。

$\varphi * I_0 = I$
$\mu * I_0 = \Delta$
$d = I_0 * I_0$
$f = \Delta * f$

性质：

$1. $ 交换律：$f * g = g * f$。

$2. $ 结合律：$f * (g * h) = (f * g) * h$

$3. $ 分配律：$f * (g + h) = (f * g) + (f * h)$

定理：若 $f, g$ 是积性函数，则 $f * g$ 也是积性函数。

观察：

\[f = \Delta * f \]

说明 $\Delta$ 在积性函数内充当了一个幺元。

而

\[\mu * I_0 = \Delta \]

则说明 $\mu, I_0$ 互为逆元。

Mobius 反演

Example 1

\[\sum_{i = 1}^{n}\sum_{j = 1}^{n}[\gcd(i, j) = 1] = \sum_{i = 1}^{n}\sum_{j = 1}^{n}\sum_{d | \gcd(i, j)}\mu(d) \]

\[= \sum_{d = 1}^{n} \mu(d)\left(\left\lfloor\frac{n}{d}\right\rfloor\right)^2 \]

Example 2

\[\sum_{i = 1}^{n}\sum_{j = 1}^{n}\gcd(i,j) = \sum_{i = 1}^{n}\sum_{j = 1}^{n}\sum_{d | \gcd(i,j)}\varphi(d) = \sum_{d = 1}^{n} \varphi (d) \left(\left\lfloor\frac{n}{d}\right\rfloor\right)^2 \]

六、生成函数

Example 1

Example 2

Example 3

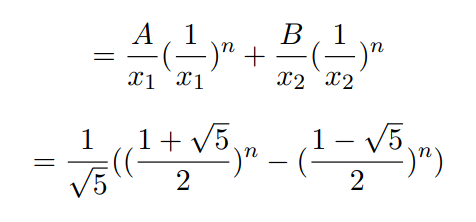
Example 4

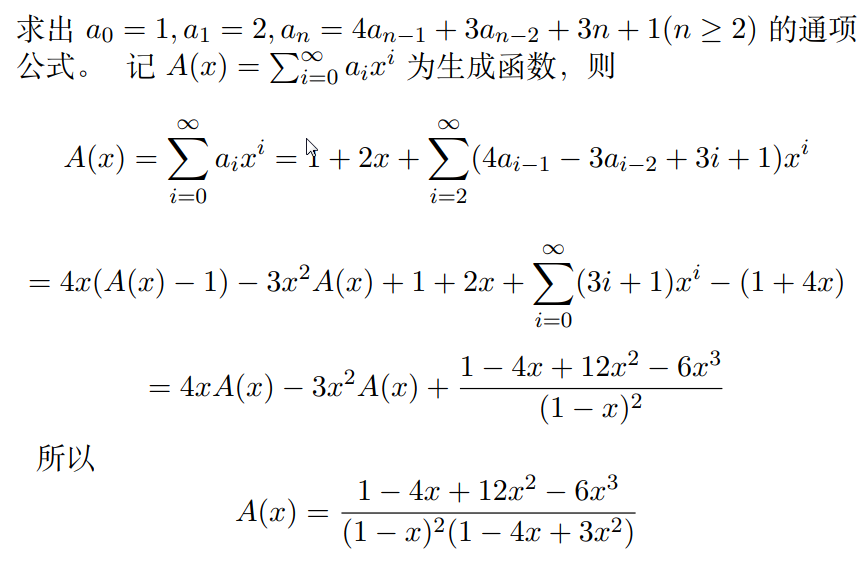
Example 5

Solution 待补充。

Example 6

Solution 1

我们考虑将左括号数量看成横坐标，右括号数量看成纵坐标，将括号序列看成路径，那么在任何时刻右括号数量不能超过左括号数量（这就是一个合法的括号序列）

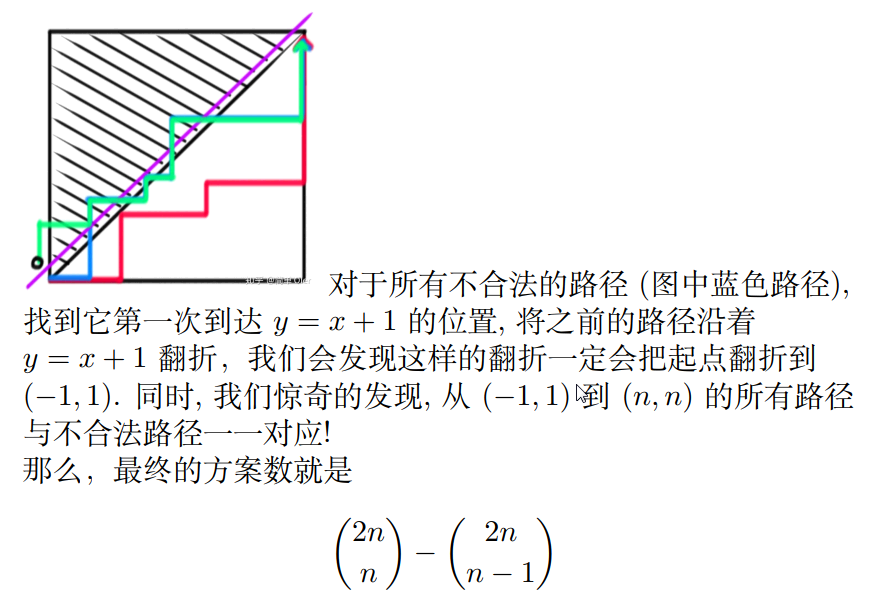
Solution 2

七、Stirling 数

第一类 Stirling 数

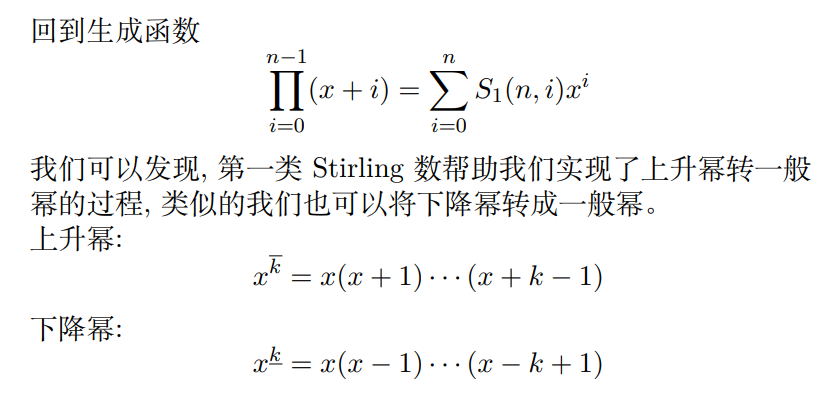
第二类 Stirling 数

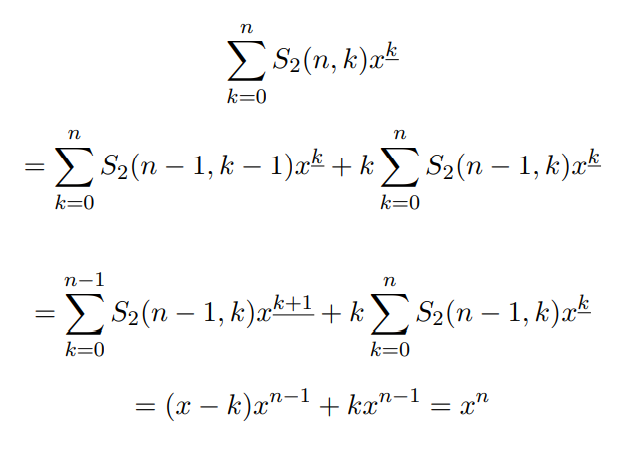
八、群论

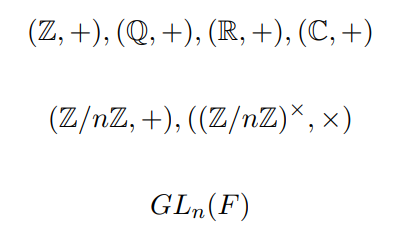
$\text{Klein }V_4$

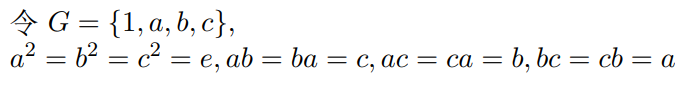
$\text{Dihedral group }D_{2n}$

置换群

生成元

元素的阶

子群

陪集

陪集定理

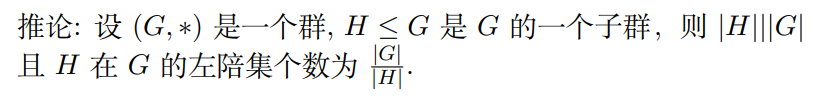
群作用

Example

轨道稳定集定理

Example

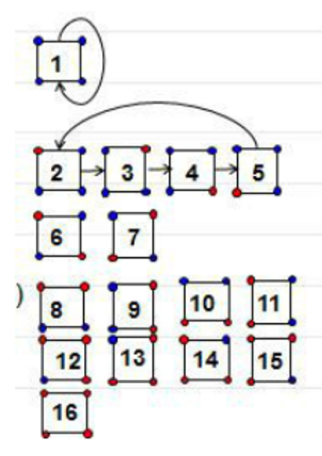
$\text{Burnside}$ 引理

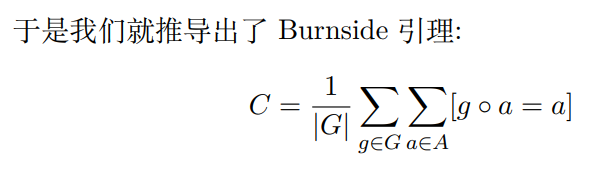
九、行列式