排序算法笔记
排序算法笔记
冒泡排序
算法介绍
冒泡排序是对于长度为 n n n 的序列,重复执行 n n n 次将 a i a_i ai 与 a i a_i ai + _+ + 1 _1 1 ( 1 ⩽ i ⩽ n − 1 ) {\color{Gray} (1 \leqslant i \leqslant n-1)} (1⩽i⩽n−1)进行比较的算法。
时间复杂度
综上所述,冒泡排序的时间复杂度是 O ( n 2 ) O(n^2) O(n2)。
动图
(与描述有细微差别)

选择排序
算法介绍
选择排序是对于长度为 n n n 的序列,先固定好需要排序的数 a i a_i ai 再寻找接下来 最小的数 a j a_j aj 与 a i a_i ai 对调 ( 1 ⩽ i < j ⩽ n ) {\color{Gray} (1 \leqslant i <j \leqslant n)} (1⩽i<j⩽n) 的算法。
时间复杂度
综上所述,选择排序的时间复杂度是 O ( n 2 ) O(n^2) O(n2)。
动图
插入排序
算法介绍
插入排序是对于长度为 n n n 的序列,先取出需要排序的数 a i a_i ai 再寻找适合其的间隙插入 ( 1 ⩽ i ⩽ n ) {\color{Gray} (1 \leqslant i \leqslant n)} (1⩽i⩽n) 的算法。
时间复杂度
综上所述,插入排序的时间复杂度是 O ( n 2 ) O(n^2) O(n2)。
动图
归并排序
算法介绍
归并排序是使用递归(分治)来实现的排序算法。归并排序对于长度为 n n n 的序列,把序列对半分进行两次递归,直至 n ⩽ 2 n \leqslant 2 n⩽2;若 n ⩽ 2 n \leqslant 2 n⩽2 则把序列进行排序;当递归程序返回时,则再把返回的数据进行排序。
时间复杂度
综上所述,归并排序的时间复杂度是 O ( n l o g n ) O(nlogn) O(nlogn)。
动图
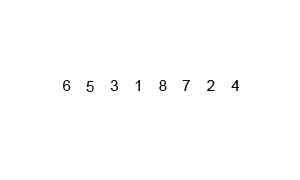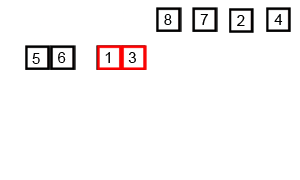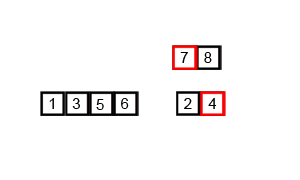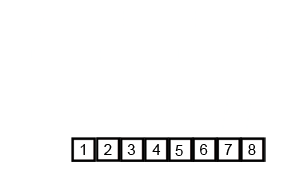
快速排序
算法介绍
快速排序是使用递归(分治)来实现的排序算法。快速排序对于长度为 n n n 的序列,先找一个基准数 a i a_i ai ,把序列小于基准数的放在基准数前面,其余的放后面,一直递归基准数前面的序列,直至基准数前面的序列长度为1,接着再递归基准数后面的数。
时间复杂度
综上所述,快速排序的时间复杂度是 O ( n 2 ) O(n^2) O(n2)。
动图
