模拟集成电路设计系列博客——2.1.2 两级放大器的频率响应

sasasatori / 2023-09-03 / 原文

2.1.2 两级放大器的频率响应

我们现在开始研究补偿电容\(C_c\)对频率响应的影响，补偿电容会在一个频率点开始引发增益幅度的减小，但仍在一个远低于单位增益频率的频点，对应于很多应用的中频点。我们使用一些简化假设，首先忽略除了补偿电容\(C_c\)以外的所有电容，其次我们认为电阻\(R_c\)不存在（这个电阻的作用是实现超前补偿，仅在放大器的单位增益频率附近起到作用）。下图我们展示了一个简化电路用于分析。

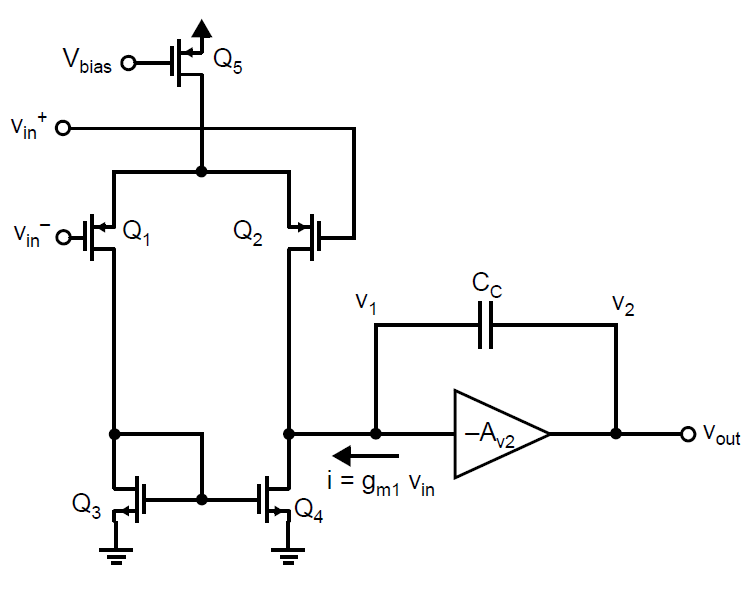
第二级通过补偿电容\(C_c\)在第一级上引入了一个电容负载。使用米勒定理可以求出节点\(v_1\)上的等效负载电容\(C_{eq}\)：

\[C_{eq}=C_c(1+A_{v2})\approx C_cA_{v2} \tag{2.1.10} \]

利用差分对的结论，有：

\[A_{v1}=\frac{v_1}{v_{in}}=-g_{m1}Z_{out1} \tag{2.1.11} \]

其中：

\[Z_{out1}=r_{ds2}||r_{ds4}||\frac{1}{sC_{eq}} \tag{2.1.12} \]

对于中频点，其输出阻抗由\(C_{eq}\)主导，我们可以计算出：

\[Z_{out1}\approx \frac{1}{sC_{eq}}\approx \frac{1}{sC_cA_{v2}} \tag{2.1.13} \]

对于整体增益：

\[A_{v}(s)=\frac{v_{out}}{v_{in}}=A_{v2}A_{v1}\approx A_{v2}\frac{g_{m1}}{sC_cA_{v2}}=\frac{g_{m1}}{sC_c} \tag{2.1.14} \]

使用\((2.1.14)\)我们可以估算出使得\(|A_v(j\omega_{ta})|=1\)的单位增益频率点\(\omega_{ta}\)的值：

\[\omega_{ta}=\frac{g_{m1}}{C_c}\tag{2.1.15} \]

注意到单位增益频率与\(g_{m1}\)成正比，与\(C_c\)成反比，进一步转换\((2.1.15)\)可以得到：

\[\omega_{ta}=\frac{2I_{D1}}{V_{eff1}C_c}=\frac{I_{D5}}{V_{eff1}C_c} \tag{2.1.16} \]

\((2.1.16)\)表明，对于固定的单位增益频率来说，偏置电流（或者说功耗）可以通过减小\(V_{eff1}\)来实现减小。选择较小的\(V_{eff1}\)的缺点是可能会增加失真，但是对于反馈中的放大器来说这种影响会得到缓解，因为工作于反馈中的放大器其差分输入端的差分信号往往非常小。\((2.1.16)\)假定了晶体管\(Q_1\)和\(Q_2\)遵从平方律，但其实单晶体管工作也亚阈值区时电流时最小的，对于亚阈值区晶体管来说有\(g_{m1(sub-th)}=qI_{D1}/nkT\)，带入到\((2.1.15)\)后有\(\omega_{ta}=qI_{D1}/nkTC_{c}\)。

例题：

假定一个两级放大器所有参数与上一小节中的例题完全一致，\(C_c=1pF\)，求单位增益频率。

解答：

使用\(g_{m1}=1.3mA/V\)，和公式\((2.1.15)\)，有：

\[\omega_{ta}=\frac{1.3\times 10^{-3}A/V}{1\times10^{-12}F}=1.3\times10^{9} rad/sec \tag{2.1.17} \]

对应的频率为\(f_{ta}=\omega_{ta}/2\pi=207MHz\)