矩阵连乘--从证明到代码实现

yuooo / 2023-05-11 / 原文

证明

以下是演示与修改

1. 假设A1=25*12， A2=12*35， A3=35*4， A4=4*17；运行dyProg(p,n,m,s)得到的最优解为：A1（A2*A3）A4，此时计算的乘法次数最少为4580；

2. 代码执行的过程如下：

需要计算的矩阵如下：

A1	A2	A3	A4
25×12	12×35	35×4	4×17

将其记录到一维数组之中p[5]：

p0	p1	p2	p3	p4
25	12	35	4	17

用r代表当前的矩阵链的长度，也就是子规模的问题，自下向上逐步求解，即是从链长为2的问题开始，逐步计算出链长为3，4的子问题的最优解，最终计算出四个矩阵连乘的最优解。

当 r=2 时，迭代计算出：

m[1:2] = m[1:1]+m[2:2}+p[0]*p[1]*p[2]；

m[2:3] = m[2:2]+m[3:3]+p[1]*p[2]*p[3];

m[3:4] = m[3:3]+m[4][4]+p[2]*p[3]*p[4];

当 r=3 时，迭代计算出：

m[1:3]=min(m[1:1]+m[2:3]+p[0]*p[1]*p[3],m[1:2]+m[3:3]+p[0]*p[2]*p[3]);

m[2:4]=min(m[2:2]+m[3:4]+p[1]*p[2]*p[4],m[2:3]+m[4:4]+p[1]*p[3]*p[4]);

当 r=4 时，计算出最终结果：

m[1:4]=min(m[1:1]+m[2:4]+p[0]*p[1]*p[4],m[1:2]+m[3:4]+p[0]*p[2]*p[4], ,m[1:3]+m[4:4]+p[0]*p[2]*p[4]);

即：

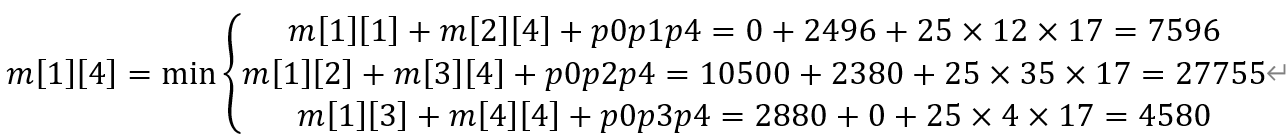
程序结果中，第一列为i的取值，第一行为j的取值：

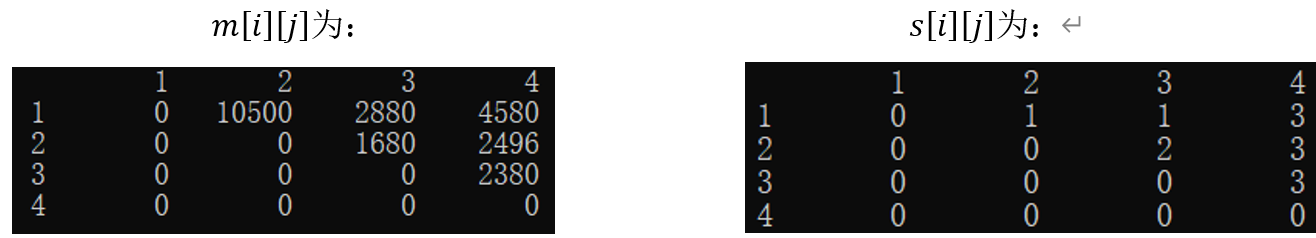
3. 修改后能显示相乘顺序的代码如下：

4.    #include <stdlib.h>   
5.    #include <stdio.h>   
6.    //---------------------------------------------------------------------------   
7.    //动态创建二维数组  
8.    template<typename T>   
9.    T **creta2Darray(int n)   
10.    {   
11.        T **p = new T *[n];   
12.        for(int i=0;i<n;i++)   
13.        {   
14.        p[i]=new int[n];   
15.        for(int j=0;j<n;j++) p[i][j] = 0;   
16.        }   
17.        return p;   
18.    }   
19.    //---------------------------------------------------------------------------   
20.    //输出二维数组，屏蔽第一维  
21.    void disp2Darray(int **p,int n)   
22.    {   
23.        for(int i=1;i<n;i++)   
24.        {   
25.            for(int j=1;j<n;j++) printf("%8d",p[i][j]);   
26.            putchar('\n');   
27.        }   
28.    }   
29.    //---------------------------------------------------------------------------   
30.    //动态规划法计算矩阵连乘的最优解  
31.    void MatrixChain(int *p,int n,int **m,int **s){   
32.        for(int i=1;i<=n;i++) m[i][i] = 0;   
33.        for(int r=2;r<=n;r++)  
34.        { //r 为当前计算的链长（子问题规模）  
35.            for(int i=1;i<=n-r+1;i++)  
36.            { //n-r+1 为最后一个 r 链的前边界  
37.                int j = i+r-1; //计算前边界为 r，链长为 r 的链的后边界  
38.                //将链 ij 划分为 A(i) * ( A[i+1:j] )   
39.                m[i][j] = m[i+1][j] + p[i-1]*p[i]*p[j];   
40.                s[i][j] = i; //记录断开点的索引  
41.                for(int k = i+1 ; k<j;k++)   
42.                {   
43.                    //将链 ij 划分为( A[i:k] )* (A[k+1:j])   
44.                    int t = m[i][k] + m[k+1][j] + p[i-1] *p[k]*p[j];   
45.                    if(t<m[i][j]) {  m[i][j] = t; s[i][j] = k;   }   
46.                }   
47.            }   
48.        }   
49.    }   
50.    //---------------------------------------------------------------------------  
51.    //构造最优解  
52.    void Traceback(int i,int j,int **s)   
53.    {   
54.        if(i==j) {  
55.            printf("A%d", i);  
56.            return;  
57.        }  
58.        putchar('(');  
59.        Traceback(i,s[i][j],s);   
60.        Traceback(s[i][j]+1,j,s);   
61.        putchar(')');  
62.    }  
63.    //---------------------------------------------------------------------------  
64.    //动态规划法   
65.    void dyProg(int *p,int n,int **m,int **s)   
66.    {   
67.        MatrixChain(p,n,m,s);   
68.        disp2Darray(m,n+1);   
69.        printf("\n");   
70.        disp2Darray(s,n+1);   
71.        printf("Optimal Parenthesization: ");  
72.        Traceback(1,n,s);   
73.        printf("\n");  
74.    }  
75.    //---------------------------------------------------------------------------  
76.    int main(int argc, char* argv[])   
77.    {  
78.        int p[] = {25,12,35,4,17};   
79.        int n = sizeof(p)/sizeof(int)-1;   
80.        int **m = creta2Darray<int>(n+1);   
81.        int **s = creta2Darray<int>(n+1);   
82.        //动态规划法  
83.        dyProg(p,n,m,s);   
84.        system("pause");   
85.        return 0;   
86.    }