[APIO2018] 铁人两项

题意：给定一个张图，询问其中有多少个有序三元组 \((u,v,w)\)，满足存在一条从 \(u\) 到 \(w\) 的简单路径，经过点 \(v\)。
考虑建出原图的圆方树。可以在圆方树上进行树形DP，分别对于圆点和方点的情况讨论即可。
复杂度可以做到 \(O(n+m)\)。

[APIO2018] 选圆圈

题意：图中有 \(n\) 个圆，按照半径从大到小的顺序删除圆，同时删去与其相交或相切的所有圆，问每一个圆是被哪一个圆删掉的。
感觉这个东西并不好数据结构维护，所以考虑暴力。
首先记当前最大的圆为 \(R\)，如果我们将整个网格分割成边长为 \(2R\) 的正方形，则只需要枚举与它所在格子及其它八连通的九个格子即可。
这样的构造使用哈希可以做到单次 \(O(n)\)。
但是这样的方格在做到足够大的时候是不优的，所以我们要考虑当前最长的半径 \(R_0<\dfrac{R}{2}\) 时，进行一次重构，我们会重构 \(O(\log W)\) 次，在每一层，它最多都会被暴力查找 \(O(1)\) 次（具体来说最多36次），所以整体复杂度会是 \(O(n\log W)\) 的。

[APIO2018] 新家

题意：有 \(n\) 家商店，每一个商店属于一个种类，且在某一段时间内在某一个位置出现。\(Q\) 次询问，求对于每一个时间点的某一位置，找到最小的 \(l\)，使得到每一种商店的最短距离均小于 \(l\)，或判断无解。
使用二分答案，题目转化为判断一个区间内是否有所有 \(k\) 种商店，同时支持插入和删除。
对于每一个商店，维护他前一个的与它种类相同的店的位置，如果 \([r,+\infty)\) 的所有点中这个值的最小值 \(\geqslant l\)，说明在 \([l,r]\) 中出现了所有 \(k\) 种商店，在 \(\pm\infty\) 处插入每一种商店各一个即可。时间复杂度 \(O(n\log^2n)\)。

[APIO2019] 桥梁

题意：给定一张图，边有边权，支持两种操作：修改一条边的边权，查询从某个点开始只经过边权 \(\geqslant v\) 的边能到达多少节点。
对操作序列进行分块，每次读入 \(B\) 个操作，将所有的询问从大到小排序，同时将所有的在 \(B\) 次操作中没有修改的边从大到小依次加入，使用并查集维护连通块。求解询问的答案是，将所有修改过权值的边扫一遍加入即可。需要使用可撤销并查集。
计算时间复杂度，单次处理，复杂度为 \(O(m\log m+m\log n+B^2\log n)\)，需要处理 \(\dfrac{q}{B}\) 次，时间复杂度为 \(O(\dfrac{q}{B}(m\log m+m\log n+B^2\log n))\)，当 \(B\) 取 \(O(\sqrt{\dfrac{m(\log m+\log n)}{\log n}})\) 时复杂度最优。

[APIO2019] 奇怪装置

题意：对于整数 \(t\)，生成有序数对 \((x,y)\)，其中 \(x=(t+\left\lfloor\dfrac{t}{B}\right\rfloor)\bmod A,y=t\bmod B\)，询问对于所有整数 \(t\in \bigcup\limits_{i=1}^n[l_i,r_i]\)，一共能生成多少个本质不同的数对。
由于 \(y\in[0,B)\) 将数对 \((x,y)\) 转化为数 \(x\times B+y\)，将 \(x,y\) 代入，即为 \(t(B+1)\bmod AB\)，考虑最小的正整数 \(t_0\)，使得 \(t_0(B+1)\equiv 0\pmod{AB}\)。
由于 \(B\) 与 \(B+1\) 互质，则 \(t_0=\dfrac{AB}{\gcd(A,B+1)}\)。
原题转化为询问原来的所有区间，有多少本质不同的 \(t\bmod t_0\)，是从离散化和差分即可，时间复杂度 \(O(n\log n)\)

[APIO2019] 路灯

题意：有一个长为 \(n\) 的 \(01\) 序列，支持两种操作：翻转单点 \(01\) 状态，查询到目前一共有多少个时刻满足 \([l,r]\) 的所有数均为 \(1\)。
维护原序列中的极长 \(1\) 串，显然为原序列中的若干个不交区间，而每一次修改只会改变至多 \(2\) 个区间，可以使用set维护（其实就和ODT很像）。
则 set 中每一个 \([l,r]\) 代表所有 \(l\leqslant l_0<r_0\leqslant r\) 均满足条件，考虑对其进行差分，在消失时加上 \(t\) 的贡献，在出现时减去 \(-t\) 的贡献。
使用线段树套动态开点线段树实现矩阵加，单点查，时间复杂度 \(O(m\log^2n)\)。

[APIO2020] 粉刷墙壁

[APIO2020] 交换城市

[APIO2020] 有趣的旅途

[APIO2021] 六边形领域

[APIO2021] 雨林跳跃

[APIO2021] 封闭道路

题意：给定一个有 \(n\) 个节点的树，边有边权，对于 \(k=0,1 \dots n-1\)，求最小的边权和使得删去这些边之后，每一个点的度数 \(\leqslant k\)。
首先，考虑对于特定的 \(k\) 进行DP，维护 \(f_{u,0/1}\) 表示在 \(u\) 节点的子树内，删/不删连向 \(u\) 的父亲。然后使用堆根据 \(f_{v,1}-f_{v,0}\) 的值从小到大排序来维护转移，这样可以做到单次 \(O(n\log n)\)，总体复杂度 \(O(n^2\log n)\)。
我们考虑降低复杂度。对于一个度数为 \(d\) 的点，对于所有 \(k\geqslant d\)，它都不需要删点，也就意味着对应的DP值就是 \(0\) 和到父亲的链的长度。
所以，我们考虑求解 \(k\) 的时候只遍历度数 \(\geqslant k\) 的点，而对于所有度数 \(<k\) 的点，只需要提前将它的转移处理到与它相邻点的堆中即可。
使用可删除堆维护，复杂度为 \(O(\sum d\log n)\) 即 \(O(n\log n)\)。

[APIO2022] 火星

[APIO2022] 游戏

[APIO2022] 排列

题意：构造一个排列，是的其递增子序列数为给定的 \(k\)。
考虑一个长为 \(n\) 的单调上升，它对答案贡献的逆序对数为 \(2^n\) 对，具体实现如下图。

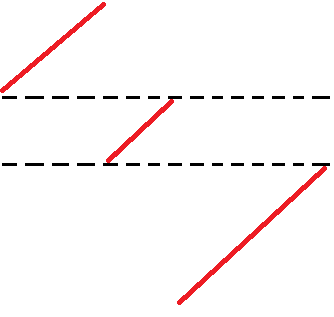
这样对于 \(k\) 进行二进制拆分，可以做到 \(B\log_2^2k\) 的序列长度，其中 \(B>1\) 无法通过。
发现我们有很多的点都在做同一件事情：使得递增子序列数 \(\times 2\)。我们可以考虑维护一个长为 \(\log_2k\) 的乘法部件，在需要的二进制位下挂一个数，表示加上对应的 \(2^n\)。实现如下图。

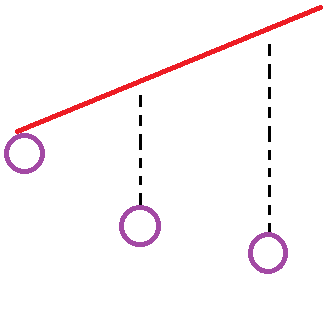
这样序列最长为 \(2\log_2k\) 的，可以拿到比较优秀的部分分。
考虑继续优化。
如果同时出现 \(2^n\) 和 \(2^{n+1}\)，我们可以将其改为 \(3\times 2^n\)。具体实现如下图。

如果蓝色和橙色的点分别对应 \(2^{n+1}\) 和 \(2^n\) 的点，我们在 \(2^n\) 处挂一个红色点在左边两个紫色点上即可。这样子的序列长度最劣是 \(1.5\log_2k+1\) 的，可以通过此题。