2023.8.18A组模拟赛总结
T1 幂矩阵
这题十分巧合。题目大意是有这样一个矩阵
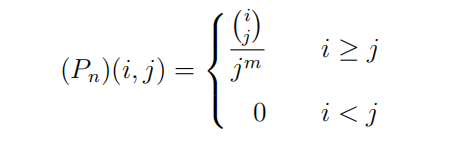
求该矩阵的逆矩阵中每项元素的平方和，手模几个点，会发现以下结论
\[(P_n)^{-1}(i,j)=
\begin{cases}
i^m\binom ij \quad i \geq j\\
0 \quad i < j
\end{cases}
\]
不难发现我们的答案即是
\[\sum_{i=1}^ni^{2m}\sum_{j=1}^i\binom ij
\]
然后发现后面这个东西我在给367天前的一场比赛出的题里用了这个式子的结论
结论是
\[\sum_{i=0}^n\binom ni=\binom{2n}n
\]
直接代入即可如果\(i^{2m}\)用线性筛处理一下可以做到\(O(n)\)但\(O(n\log m)\)能过所以就懒得写了
#include<bits/stdc++.h>
#define fre(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout)
using namespace std;
typedef long long LL;
const LL mod=1e9+7;
const int N=3e6;
LL fpow(LL a,LL b){LL ret=1;
for(;b;b>>=1,a=a*a%mod)
if(b&1)ret=ret*a%mod;
return ret;
}
LL fac[N+5],inv[N+5];
void init(){fac[0]=1;
for(int i=1;i<=N;i++)fac[i]=fac[i-1]*i%mod;
inv[N]=fpow(fac[N],mod-2);
for(int i=N;i;i--)inv[i-1]=inv[i]*i%mod;
}
LL C(int n,int m){
return fac[n]*inv[m]%mod*inv[n-m]%mod;
}
int main(){
init();
int n,m;scanf("%d%d",&n,&m);
LL ans=0;
for(int i=1;i<=n;i++)
ans+=(C(2*i,i)+mod-1)*fpow(i,2*m)%mod,ans%=mod;
printf("%lld",ans);
return 0;
}
T2 Game
现在XC拼题水平越来越高了，一场比赛用之前四场的题拼，这题大意是说给\(A\)，\(B\)两个数组把\(B\)数组重新排列，最大化\(\sum[B_i>A_i]\)，并同时最大化\(B\)的字典序。
考场写个20pts暴力走了。
正解是贪心+线段树。
首先答案用一个权值线段树维护答案。
从第1到n位顺序考虑，我们设去掉\(a_i\)后答案不变。
假设\(ls0\)表示去掉\(a_i\)后在线段树的匹配中最大的匹配成功的\(b\)，\(ls1\)表示最大的未被匹配的\(b\)。
- 先考虑去掉\(a_i\)答案不变的情况。
- \(ls0\le a_i\)，那么\(ls1\le a_i\)（否则\(ls1\)和\(a_i\)匹配与假设不符），\(a_i\)和\(ls1\)匹配
- \(ls0>a_i\)，我们就让\(ls0\)和\(a_0\)匹配，舍弃原来的匹配，使字典序更大。
- 去掉\(a_i\)答案变小的话，那我们就必须选\(ls1\)了
#include<bits/stdc++.h>
#define fre(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout)
using namespace std;
const int N=2e5+5;
int t0[N],t1[N];
#define lson p<<1
#define rson p<<1|1
int T[N<<2],T0[N<<2],T1[N<<2];
void Up(int p){
int k=min(T0[lson],T1[rson]);
T[p]=T[lson]+T[rson]+k;
T0[p]=T0[lson]+T0[rson]-k;
T1[p]=T1[lson]+T1[rson]-k;
}
void build(int p,int l,int r){
if(l==r){T0[p]=t0[l],T1[p]=t1[l],T[p]=0;return;}
int mid=l+r>>1;build(lson,l,mid),build(rson,mid+1,r);
Up(p);
}
void modif(int p,int l,int r,int w,int op){
if(l==r){if(op)T1[p]--;else T0[p]--;return;}
int mid=l+r>>1;
if(w<=mid)modif(lson,l,mid,w,op);
else modif(rson,mid+1,r,w,op);
Up(p);
}
int ask(int p,int l,int r,int op,int d=0){
if(l==r)return l;
int mid=l+r>>1;
int ret=max(d-T1[lson],0)+T0[lson];
if(op){
if(T[rson]||min(ret,T1[rson]))return ask(rson,mid+1,r,op,ret);
else return ask(lson,l,mid,op,d);
}else{
if(ret<T1[rson])return ask(rson,mid+1,r,op,ret);
else return ask(lson,l,mid,op,d);
}
}
#undef lson
#undef rson
int a[N],b[N],w[N],m,n;
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d",&a[i]),w[++m]=a[i];
for(int i=1;i<=n;i++)scanf("%d",&b[i]),w[++m]=b[i];
sort(w+1,w+m+1);
m=unique(w+1,w+m+1)-w;
for(int i=1;i<=n;i++)
a[i]=lower_bound(w+1,w+m+1,a[i])-w,t0[a[i]]++;
for(int i=1;i<=n;i++)
b[i]=lower_bound(w+1,w+m+1,b[i])-w,t1[b[i]]++;
build(1,0,m);
for(int i=1;i<=n;i++){
int lst=T[1],k;
modif(1,0,m,a[i],0);
if(T[1]==lst){
int l=ask(1,0,m,1),r=ask(1,0,m,0);
if(l<=a[i])k=r;else k=l;
}
else k=ask(1,0,m,0);
printf("%d ",w[k]);
modif(1,0,m,k,1);
}
return 0;
}
T3 方阵移动
考场没想到，最佳匹配用费用流这么基本的东西都忘了，应该好好复习网络流了。
猜到答案是单凸的，直接三分，然后暴力连边，然后跑费用流即可（%%%hefenghhhh，他教我们的zkw费用流，现在在“市面“上没见过如此nb的写法），时间复杂度\(O(n^7\log A)\)，如果写km的话可以做到\(O(n^6\log A)\)，但一般最佳匹配不这么卡，所以练好网络流。
#include<bits/stdc++.h>
#define fre(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout)
using namespace std;
typedef long long LL;
const LL Inf=0x3f3f3f3f3f3f3f3f;
const int N=10*10*2;
struct Edge{
int Nxt,To;LL val,r;
}Ed[N*N*4];
int Head[N],Cnt;
void Add(int u,int v,int val,LL r){
Ed[++Cnt]={Head[u],v,val,r};
Head[u]=Cnt;
}
int tot,s,t;
LL ret=0;
bool vis[N];
LL dis[N],ans;
LL aug(int x,LL augc){
if(x==t){ans+=dis[s]*augc;return augc;}
LL tr=augc,del;vis[x]=1;
for(int i=Head[x];i&&tr;i=Ed[i].Nxt)
if(Ed[i].val>0&&!vis[Ed[i].To])
if(Ed[i].r+dis[Ed[i].To]==dis[x]){
del=aug(Ed[i].To,min(Ed[i].val,tr));
Ed[i].val-=del,Ed[i^1].val+=del,tr-=del;
}
return augc-tr;
}
bool rebui(){
LL mn=Inf;
for(int i=1;i<=tot;i++)
if(vis[i])for(int j=Head[i];j;j=Ed[j].Nxt)
if(!vis[Ed[j].To]&&Ed[j].val>0)
mn=min(mn,Ed[j].r+dis[Ed[j].To]-dis[i]);
if(mn==Inf)return 0;
for(int i=1;i<=tot;i++)
if(vis[i])dis[i]+=mn;
return 1;
}
LL flow(){
int flow,now;ans=0;
do{do{
memset(vis,0,sizeof(vis));
now=aug(s,Inf);
flow+=now;
}
while(now);}while(rebui());
return ans;
}
int n,p;
LL x[N],y[N];
LL check(int mid){
memset(dis,0,sizeof(dis));
memset(Head,0,sizeof(Head));Cnt=1,tot=n*n;
for(int i=0;i<n;i++)
for(int j=mid;j<mid+n;j++)
x[++tot]=i,y[tot]=j;
s=++tot,t=++tot;
for(int i=1;i<=n*n;i++)
Add(s,i,1,0),Add(i,s,0,0);
for(int i=1;i<=n*n;i++)
Add(i+n*n,t,1,0),Add(t,i+n*n,0,0);
for(int i=1;i<=n*n;i++)
for(int j=1;j<=n*n;j++){
LL dis=abs(x[i]-x[j+n*n])+abs(y[i]-y[j+n*n]);
if(p>1)dis=dis*dis;
Add(i,j+n*n,1,dis);
Add(j+n*n,i,0,-dis);
}
return flow();
}
int main(){
int T;scanf("%d",&T);
while(T--){
scanf("%d%d",&n,&p);
for(int i=1;i<=n*n;i++)
scanf("%lld%lld",&x[i],&y[i]);
int l=-2e6,r=2e6;
while(r-l>=5){
int mid1=(l+r)/2;
int mid2=mid1+1;
if(check(mid1)<check(mid2))r=mid2;
else l=mid1;
}
LL Ans=Inf;
for(int i=l;i<=r;i++)
Ans=min(Ans,check(i));
printf("%lld\n",Ans);
}
return 0;
}
T4 决心
没补，之前好像做过一次，但集体该题爆0