普及模拟1
普及模拟1

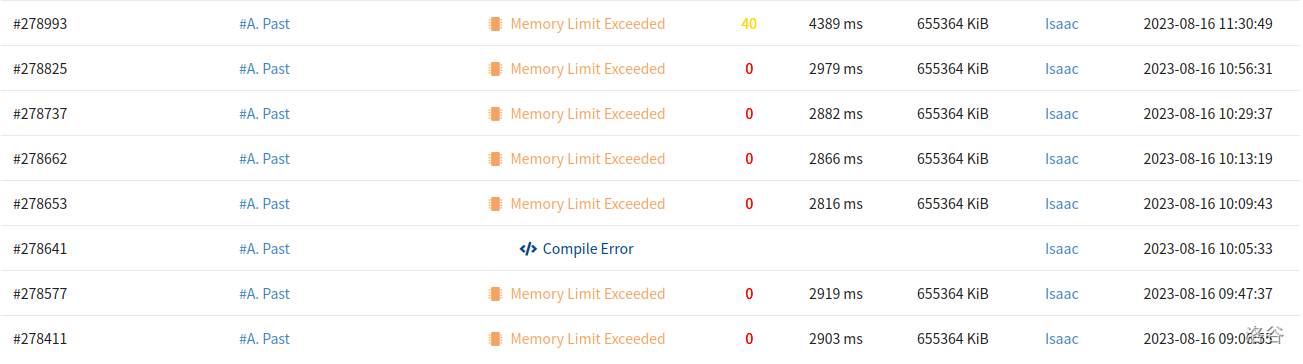
T1 Past \(0pts\)

-
部分分:
- \(O(n^3)\) 暴力枚举:\(TLE\) \(50pts\)
- \(O(n^2+n \times log_2(n))\)
-
线段树维护极差:\(TLE\) \(50pts\)
-
\(ST\) 表维护极差:\(MLE+TLE\) \(40pts\)
- \(ST\) 表数组开太大了,全部 \(MLE\) 挂了 \(40pts\)。
-
-
正解:
- \(d=1\) 时,打表发现第 \(i\) 个数对答案产生的贡献为 \(a_i \times i \times (n-i+1)\) 。
- 证明:
- \(d=2\) 时,原题为luogu P6503 [COCI2010-2011#3] DIFERENCIJA。
- \(d=3\) 时,
- \(d=1\) 时,打表发现第 \(i\) 个数对答案产生的贡献为 \(a_i \times i \times (n-i+1)\) 。
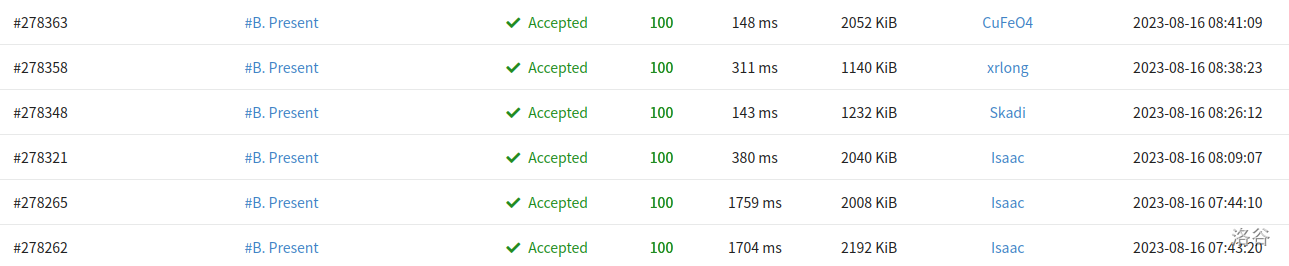
T2 Present \(100pts\)
-
luogu B3656 【模板】双端队列 1 变形,用数组模拟或 \(deque\) 维护数列,考虑开一个 \(bool\) 类型的 \(flag\) 记录是否进行颠倒。
- 每次颠倒时,将 \(flag\) 取反即可。
#include<bits/stdc++.h> using namespace std; #define ll long long #define sort stable_sort #define endl '\n' deque<ll>q; int main() { freopen("prs.in","r",stdin); freopen("prs.out","w",stdout); ll n,id,pd,x,i; bool flag=false; scanf("%lld%lld",&n,&id); for(i=1;i<=n;i++) { scanf("%lld",&pd); if(pd==0) { scanf("%lld",&x); if(flag==false) { q.push_front(x); } else { q.push_back(x); } } if(pd==1) { if(q.empty()==0) { if(flag==false) { printf("%lld\n",q.front()); q.pop_front(); } else { printf("%lld\n",q.back()); q.pop_back(); } } else { printf("0\n"); } } if(pd==2) { scanf("%lld",&x); if(flag==false) { q.push_back(x); } else { q.push_front(x); } } if(pd==3) { if(q.empty()==0) { if(flag==false) { printf("%lld\n",q.back()); q.pop_back(); } else { printf("%lld\n",q.front()); q.pop_front(); } } else { printf("0\n"); } } if(pd==4) { flag=(!flag); } } return 0; } -
貌似是首A。
T3 Future \(100pts\)
-
类似luogu P1807 最长路 ,但本题是一棵树,跑 树形 \(DP\) , \(SPFA\) , 拓扑优化 \(DP\) 求最长路 等做法皆可。
- 树形 \(DP\) 的一种做法,令 \(dp[i]\) 表示以 \(i\) 为终点时,所得到的收获值,则有状态转移方程 \(dp[i]=dp[f[i]]+w[i]\) 。
-
坑:点权有负数,输出结果应初始化为 \(-\infty\) 。
- 最后 \(40min\) 检查时才发现,差点挂了 \(10pts\) 。

#include<bits/stdc++.h> using namespace std; #define ll long long #define sort stable_sort #define endl '\n' struct node { ll nxt,to; }e[400001]; ll w[400001],f[400001],head[400001],dout[400001],cnt=0;//注意与上文数组定义不同 void add(ll u,ll v) { cnt++; e[cnt].nxt=head[u]; e[cnt].to=v; head[u]=cnt; } void dfs(ll x,ll fa) { f[x]=f[fa]+w[x]; for(ll i=head[x];i!=0;i=e[i].nxt) { if(e[i].to!=fa) { dfs(e[i].to,x); } } } int main() { freopen("ftr.in","r",stdin); freopen("ftr.out","w",stdout); ll n,i,u,ans=-0x7f7f7f7f; scanf("%lld",&n); for(i=1;i<=n;i++) { scanf("%lld",&w[i]); } for(i=1;i<=n;i++) { scanf("%lld",&u); add(u,i); dout[u]++;//统计出度,为了找到终点 } dfs(1,0); for(i=1;i<=n;i++) { if(dout[i]==0) { ans=max(ans,f[i]); } } printf("%lld\n",ans); return 0; }
T4 Beyond \(0pts\)
- \(2 \le n \le 20\)
- 部分分:
- \(10pts\) :输出
0
- \(10pts\) :输出
- 正解:考虑爆搜(明显的暗示,其实是 \(meet\) \(in\) \(middle\) ),分别从 \((1,1),(n,n)\) 进行爆搜,当到达绿色区域(当下)时,将所得到的值分别用两个 \(map\) 进行存储,又因为在绿色区域(当下)可以进行传送至另一个绿色区域(当下),然后利用加法原理和乘法原理求解。
- 对于每个 \(past\) 在 \(future\) 中用 \(map\) 的 \(.find()\) 或其他方式寻找 \(past+fate\) 出现的次数,即可进行求解。
#include<bits/stdc++.h> using namespace std; #define ll long long #define sort stable_sort #define endl '\n' ll c[21][21],f[21][21],dil[2][2]={{1,0},{0,1}},dir[2][2]={{-1,0},{0,-1}}; map<ll,ll>l,r; map<ll,ll>::iterator it,val; void dfs1(ll x,ll y,ll n,ll num) { if(y==n-x+1) { l[num]++; } else { ll i,nx,ny; for(ll i=0;i<=1;i++) { nx=x+dil[i][0]; ny=y+dil[i][1]; if(1<=nx&&nx<=n&&1<=ny&&ny<=n) { dfs1(nx,ny,n,num^c[nx][ny]); } } } } void dfs2(ll x,ll y,ll n,ll num) { if(y==n-x+1) { r[num]++; } else { ll i,nx,ny; for(ll i=0;i<=1;i++) { nx=x+dir[i][0]; ny=y+dir[i][1]; if(1<=nx&&nx<=n&&1<=ny&&ny<=n) { dfs2(nx,ny,n,num^c[nx][ny]); } } } } int main() { freopen("byd.in","r",stdin); freopen("byd.out","w",stdout); ll n,fate,i,j,ans=0,sum; scanf("%lld%lld",&n,&fate); for(i=1;i<=n;i++) { for(j=1;j<=n;j++) { scanf("%lld",&c[i][j]); } } dfs1(1,1,n,0); dfs2(n,n,n,0); for(it=l.begin();it!=l.end();it++) { val=r.find(it->first+fate); if(val!=r.end()) { ans+=(it->second)*(val->second);//将两个数出现的次数相乘 } } printf("%lld\n",ans); return 0; }
总结
-
十年 \(OI\) 一场空,不开 \(long\) \(long\) 见祖宗。
-
本次开题顺序: \((T2,T3,T1,T4)\) ,在这里没有掉进出题人的坑里


-
\(T4\) 没有再认真想想,如果想到爆搜的话可能分数再高点(?)。
-
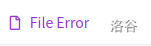
注意文件输入输出(有人在这里爆零了)。
后记
