整数划分问题（完全背包）（总方案数和最小方案数）

彦辰kkkkk / 2023-08-16 / 原文

完全背包解决整数划分问题：

总方案数：

完全背包:在前i个数中选，且总和恰好等于j的方案数
f[i][j] = f[i - 1][j] + f[i - 1][j - v]

化成一维：

f[j] += f[j - v];

这种求总方案数的情况需要把f初始化为0，然后f[0]初始化为1，最后累加f[j]

900. 整数划分

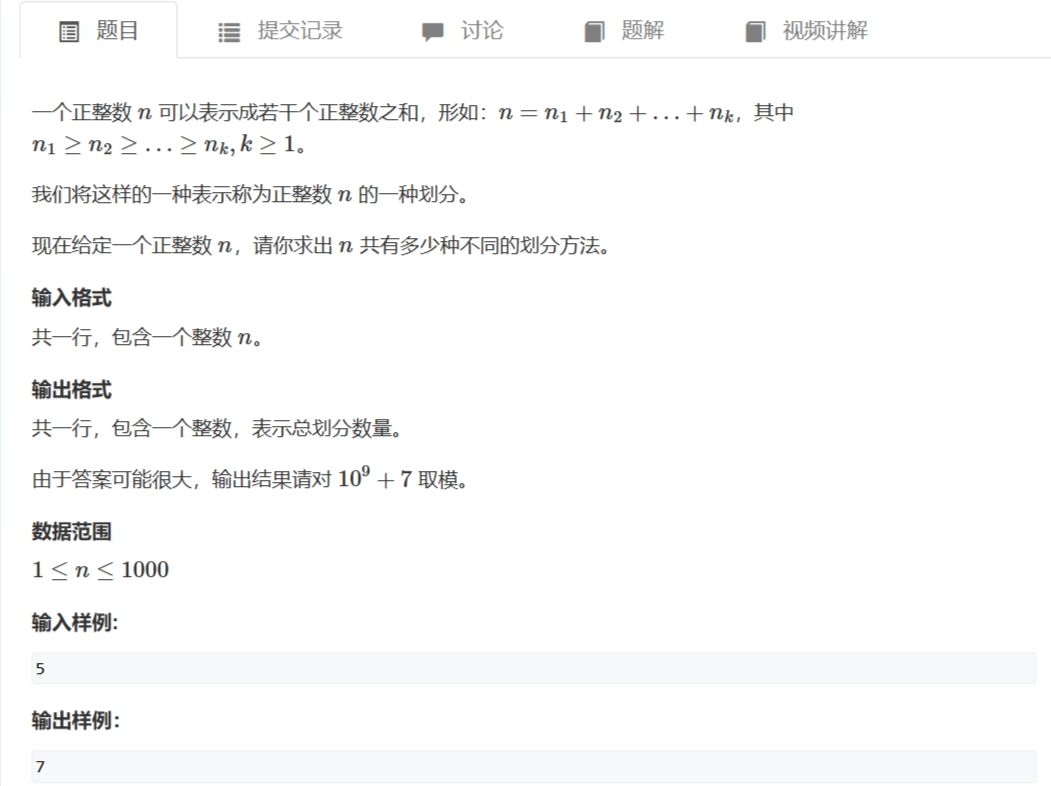
这里从小到大枚举i，用到的v就是枚举的i

#include <bits/stdc++.h>

using namespace std;

const int N = 1010, mod = 1e9 + 7;

int n;
int f[N];

int main()
{
    cin >> n;
    f[0] = 1;
    for(int i = 1; i <= n; i ++ )
        for(int j = i; j <= n; j ++ )
            f[j] = (f[j] + f[j - i]) % mod;

    cout << f[n] << endl;

    return 0;
}

最小方案数：

在前i个数中选，最后总和为j需要最少多少个数

一维：f[j] = min(f[j], f[j - v] + 1)

解释：总和为j时不选第i个数，总和为j时选第i个数（选第i个数前是f[j - v]，选完第i个数后答案需要 + 1，代表选了1个第i个数），两者取最小值。

最小方案这种情况需要把f初始化为0x3f，f[0]初始化为0

279. 完全平方数

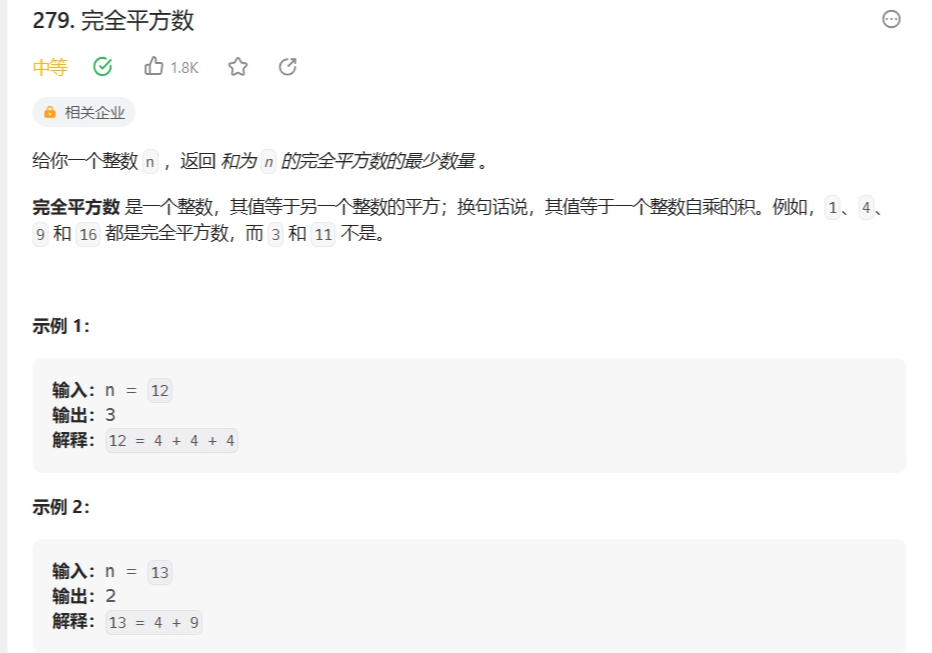
class Solution {
int f[10010];
public:
    int numSquares(int n) {
        memset(f, 0x3f, sizeof f);
        f[0] = 0;
        for(int i = 1; i <= n / i; i ++ )
        {
            int v = i * i;
            for(int j = v; j <= n; j ++ )
                f[j] = min(f[j], f[j - v] + 1);
        }
        return f[n];
    }
};

322. 零钱兑换

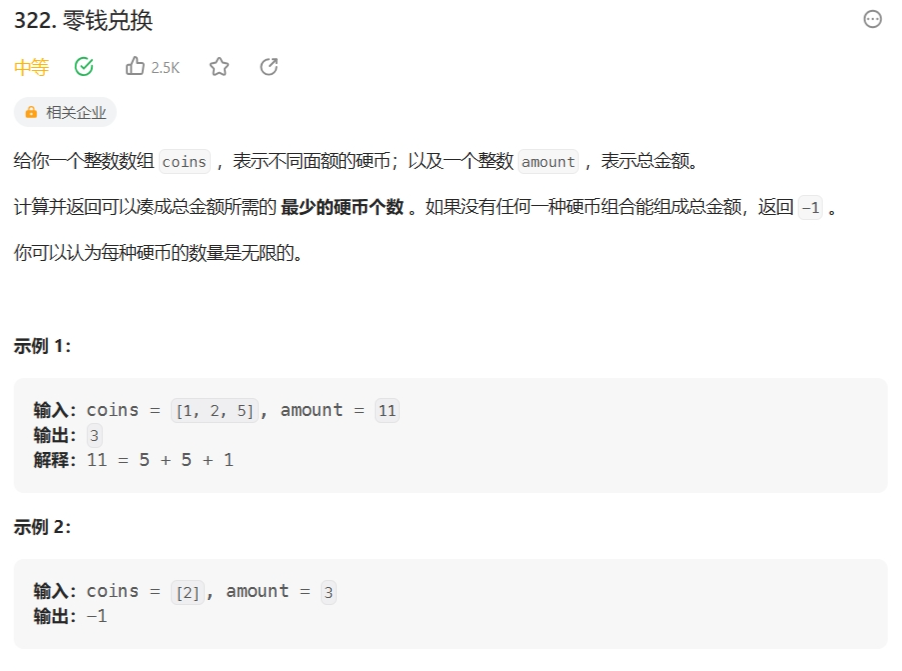
class Solution {
int f[100010];
public:
    int coinChange(vector<int>& coins, int amount) {
        memset(f, 0x3f, sizeof f);
        f[0] = 0;
        int n = coins.size();
        for(int i = 0; i < n; i ++ )
        {
            int v = coins[i];
            for(int j = v; j <= amount; j ++ )
                f[j] = min(f[j], f[j - v] + 1);
        }
        if(f[amount] == 0x3f3f3f3f) return -1;
        return f[amount];
    }
};